Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1973.
Graphs and Hypergraphs.
Vol. 6,
Issue. ,
p.
498.
Weinstein, J.
1974.
Large Matchings in Graphs.
Canadian Journal of Mathematics,
Vol. 26,
Issue. 6,
p.
1498.
Chvátal, V
and
Hanson, D
1976.
Degrees and matchings.
Journal of Combinatorial Theory, Series B,
Vol. 20,
Issue. 2,
p.
128.
Simonovits, Miklós
1997.
The Mathematics of Paul Erdös II.
Vol. 14,
Issue. ,
p.
148.
Thomason, Andrew
2008.
Disjoint unions of complete minors.
Discrete Mathematics,
Vol. 308,
Issue. 19,
p.
4370.
Allen, Peter
Böttcher, Julia
Hladký, Jan
and
Piguet, Diana
2011.
A density Corrádi-Hajnal theorem.
Electronic Notes in Discrete Mathematics,
Vol. 38,
Issue. ,
p.
31.
Grosu, Codruţ
and
Hladký, Jan
2012.
The extremal function for partial bipartite tilings.
European Journal of Combinatorics,
Vol. 33,
Issue. 5,
p.
807.
Simonovits, Miklós
2013.
The Mathematics of Paul Erdős II.
p.
245.
Allen, Peter
Böttcher, Julia
Hladký, Jan
and
Piguet, Diana
2015.
A Density Corrádi–Hajnal Theorem.
Canadian Journal of Mathematics,
Vol. 67,
Issue. 4,
p.
721.
Yuan, Long-Tu
and
Zhang, Xiao-Dong
2017.
The Turán number of disjoint copies of paths.
Discrete Mathematics,
Vol. 340,
Issue. 2,
p.
132.
Jin, Ya-Lei
and
Zhang, Xiao-Dong
2018.
The number of maximal cliques and spectral radius of graphs with certain forbidden subgraphs.
Discrete Mathematics, Algorithms and Applications,
Vol. 10,
Issue. 06,
p.
1850071.
Gerbner, Dániel
Methuku, Abhishek
and
Vizer, Máté
2019.
Generalized Turán problems for disjoint copies of graphs.
Discrete Mathematics,
Vol. 342,
Issue. 11,
p.
3130.
Lan, Yongxin
Li, Tao
Shi, Yongtang
and
Tu, Jianhua
2019.
The Turán number of star forests.
Applied Mathematics and Computation,
Vol. 348,
Issue. ,
p.
270.
Yuan, Long‐Tu
and
Zhang, Xiao‐Dong
2021.
Turán numbers for disjoint paths.
Journal of Graph Theory,
Vol. 98,
Issue. 3,
p.
499.
Yuan, Long-Tu
2022.
Extremal graphs for edge blow-up of graphs.
Journal of Combinatorial Theory, Series B,
Vol. 152,
Issue. ,
p.
379.
Chen, Wanfang
Lu, Changhong
and
Yuan, Long-Tu
2022.
Extremal Graphs for Two Vertex-Disjoint Copies of a Clique.
Graphs and Combinatorics,
Vol. 38,
Issue. 3,
Zhang, Lin-Peng
and
Wang, Ligong
2022.
The Turán Numbers of Special Forests.
Graphs and Combinatorics,
Vol. 38,
Issue. 3,
Li, Shuchao
Yu, Yuantian
and
Zhang, Huihui
2023.
An A-spectral Erdős-Pósa theorem.
Discrete Mathematics,
Vol. 346,
Issue. 9,
p.
113494.
Zhang, Junxue
2023.
Extremal numbers of disjoint triangles in r-partite graphs.
Discrete Mathematics,
Vol. 346,
Issue. 9,
p.
113530.
Liying, Kang
Yisai, Xue
and
Erfang, Shan
2024.
The Turán numbers of two kinds of Berge hypergraphs.
SCIENTIA SINICA Mathematica,
Vol. 54,
Issue. 11,
p.
1807.

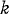 modes is called a
modes is called a 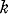 -graph
-graph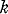 -graphs contained in a given graph
-graphs contained in a given graph 