Hostname: page-component-6bf8c574d5-mcfzb Total loading time: 0 Render date: 2025-03-09T15:56:06.989Z Has data issue: false hasContentIssue false
  • English
  • Français

On Littlewood Polynomials with Prescribed Number of Zeros Inside the Unit Disk

Published online by Cambridge University Press:  20 November 2018

Peter Borwein ,
Stephen Choi ,
Ron Ferguson  and
Jonas Jankauskas
Peter Borwein
Affiliation:
Department of Mathematics, Simon Fraser University, 8888 University Drive, Burnaby, BC V5A 1S6 e-mail: pborwein@sfu.ca, schoia@sfu.ca, ronf@sfu.ca
Stephen Choi
Affiliation:
Department of Mathematics, Simon Fraser University, 8888 University Drive, Burnaby, BC V5A 1S6 e-mail: pborwein@sfu.ca, schoia@sfu.ca, ronf@sfu.ca
Ron Ferguson
Affiliation:
Department of Mathematics, Simon Fraser University, 8888 University Drive, Burnaby, BC V5A 1S6 e-mail: pborwein@sfu.ca, schoia@sfu.ca, ronf@sfu.ca
Jonas Jankauskas
Affiliation:
Department of Mathematics and Informatics, Vilnius University, Naugarduko 24, Vilnius LT–03225, Lithuaniajonas.jankauskas@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate the numbers of complex zeros of Littlewood polynomials 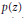$p\left( z \right)$ (polynomials with coefficients {−1, 1}) inside or on the unit circle 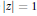$\left| z \right|\,=\,1$, denoted by 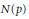$N\left( p \right)$ and 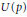$U\left( p \right)$, respectively. Two types of Littlewood polynomials are considered: Littlewood polynomials with one sign change in the sequence of coefficients and Littlewood polynomials with one negative coefficient. We obtain explicit formulas for 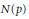$N\left( p \right)$, 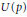$U\left( p \right)$ for polynomials 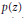$p\left( z \right)$ of these types. We show that if 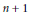$n\,+\,1$ is a prime number, then for each integer 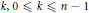$k,\,0\,⩽\,k\,⩽\,n-1$, there exists a Littlewood polynomial 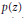$p\left( z \right)$ of degree 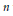$n$ with 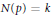$N\left( p \right)\,=\,k$ and 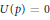$U\left( p \right)\,=\,0$. Furthermore, we describe some cases where the ratios 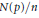$N\left( p \right)/n$ and 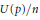$U\left( p \right)/n$ have limits as 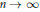$n\,\to \,\infty $ and find the corresponding limit values.

Keywords

11R0611R0911C08Littlewood polynomialszeroscomplex roots
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 67 , Issue 3 , 01 June 2015 , pp. 507 - 526
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Akhtari, S. and Choi, S. K. K., On the Littkwood cyclotomic polynomials. J. Number Theory 128(2008), no. 4, 884–894.http://dx.doi.org/10.1016/j.jnt.2007.02.010 Google Scholar
[2] Bloch, A. and Pólya, G., On roots of certain algebraic equations. Proc. London Math. Soc,S2–33(1932), 102–114.http://dx.doi.Org/10.1112/plms/s2-33.1.102 Google Scholar
[3] Borwein, P. and Choi, S. K. K., On cyclotomic polynomials with ±1 coefficients. Experiment. Math. 8(1999), no. 4, 399–407. http://dx.doi.org/10.1080/10586458.1999.10504628 Google Scholar
[4] Borwein, P. and Erdélyi, T., On the zeros of polynomials with restricted coefficients. Illinois J. Math. 41(1997), 667–675.Google Scholar
[5] Borwein, P. and Erdélyi, T., Lower bounds for the number of zeros of cosine polynomials in the period: a problem of Littlewood. Acta Arith. 128(2007), no. 4, 377–384. http://dx.doi.org/10.4064/aa128-4-5 Google Scholar
[6] Borwein, P., Erdélyi, T., Ferguson, R., and Lockhart, R., On the zeros of cosine polynomials: solution to a problem of Littlewood. Ann. of Math. 167(2008), no. 3, 1109–1117. http://dx.doi.Org/10.4007/annals.2008.167.1109 Google Scholar
[7] Borwein, P., Erdélyi, T., and Littmann, F., Polynomials with coefficients from a finite set. Trans. Amer. Math. Soc. 360(2008), no. 10, 5145–5154.http://dx.doi.org/10.1090/S0002-9947-08-04605-9 Google Scholar
[8] Boyd, D. W., Small Salem numbers. Duke Math. J. 44(1977), no. 2, 315–328.http://dx.doi.org/10.1215/S0012-7094-77-04413-1 Google Scholar
[9] Conrey, B., Granville, A., Poonen, B., and Soundararajan, K., Zeros of Feketepolynomials. Ann. Inst. Fourier (Grenoble) 50(2000), no. 3, 865–889. http://dx.doi.Org/10.58O2/aif.l776 Google Scholar
[10] Drungilas, P., Unimodular roots of reciprocal Littkwood polynomials. J. Korean Math. Soc. 45(2008), no. 3, 835–840. http://dx.doi.org/10.4134/JKMS.2008.453.835 Google Scholar
[11] Erdősand, P. Turán, P., On the distribution of roots of polynomials. Ann. of Math. 51(1950), 105–119. http://dx.doi.Org/10.2307/1969500 Google Scholar
[12] Kovanlina, J. and Matache, V., Palindrome–polynomials with roots in the unit circle. C.R. Math. Acad. Sci. Soc. R. Can. 26(2004), 39–44.Google Scholar
[13] Kronecker, L., Zwei Sätze über Gleichungen mitganzzahligen Coefficienten. J. Reine Angew. Math. 53(1857), 173–175.Google Scholar
[14] Littlewood, J. E., On the mean values of certain trigonometric polynomials. J. London Math. Soc. 36(1961), 307–334.http://dx.doi.Org/10.1112/jlms/s1-36.1.307 Google Scholar
[15] Littlewood, J. E., On the real roots of real trigonometric polynomials. II. J. London Math. Soc. 39(1964), 511–532.http://dx.doi.Org/10.1112/jlms/s1-39.1.511 Google Scholar
[16] Littlewood, J. E., On polynomials . J London Math. Soc. 41(1966), 367–376.http://dx.doi.Org/10.1112/jlms/s1-41.1.367 Google Scholar
[17] Littlewood, J. E., The real zeros and value distributions of real trigonometric polynomials. J. London Math. Soc. 41(1966), 336–342. http://dx.doi.Org/10.1112/jlms/s1-41.1.336 Google Scholar
[18] Littlewood, J. E., Some problems in real and complex analysis. Heath Mathematical Monographs, D. C. Heath and Co. Raytheon Education Co., Lexington, Mass., 1968.Google Scholar
[19] Mercer, I. D., Unimodular roots of special Littlewood polynomials. Canad. Math. Bull. 49(2006), no. 3, 438–447. http://dx.doi.Org/10.4153/CMB-2006-043-X Google Scholar
[20] Mossinghoff, M. J., Pinner, C. G., and Vaaler, J. D., Perturbing polynomials with all their roots on the unit circle. Math. Comp. 67(1998), no. 224, 1707–1726. http://dx.doi.org/10.1090/S0025-5718-98-01007-2 Google Scholar
[21] Mukunda, K., Littlewood Pisot numbers. J.Number Theory 117(2006), no. 1, 106–121.http://dx.doi.Org/10.1016/j.jnt.2005.05.009 Google Scholar
[22] Mukunda, K., Pisot and Salem numbers from polynomials of height 1. PhD Thesis, Simon Fraser University, 2006.Google Scholar
[23] Schur, I., Unteruchungen iiber algebraische Gleichungen. Sitz. Preuss. Akad. Wiss., Phys.-Math. Kl. (1933), 403–428.Google Scholar
[24] Szegő, G., Bemerkungen zu einem Satz von E. Schmidt iiber algebraische Gleichungen. Sitz Preuss. Akad. Wiss., Phys.-Math. Kl. (1934), 86–98.Google Scholar