Article contents
On 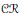 $\mathcal{C}\mathcal{R}$-Epic Embeddings and Absolute
$\mathcal{C}\mathcal{R}$-Epic Embeddings and Absolute 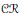 $\mathcal{C}\mathcal{R}$-Epic Spaces
$\mathcal{C}\mathcal{R}$-Epic Spaces
Published online by Cambridge University Press: 20 November 2018
Abstract
We study Tychonoff spaces 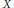 $X$ with the property that, for all topological embeddings
$X$ with the property that, for all topological embeddings 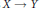 $X\,\to \,Y$, the induced map
$X\,\to \,Y$, the induced map 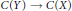 $C(Y)\,\to \,C(X)$ is an epimorphism of rings. Such spaces are called absolute
$C(Y)\,\to \,C(X)$ is an epimorphism of rings. Such spaces are called absolute 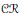 $\mathcal{C}\mathcal{R}$-epic. The simplest examples of absolute
$\mathcal{C}\mathcal{R}$-epic. The simplest examples of absolute 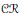 $\mathcal{C}\mathcal{R}$-epic spaces are
$\mathcal{C}\mathcal{R}$-epic spaces are  $\sigma $-compact locally compact spaces and Lindelöf
$\sigma $-compact locally compact spaces and Lindelöf  $P$-spaces. We show that absolute
$P$-spaces. We show that absolute 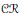 $\mathcal{C}\mathcal{R}$-epic first countable spaces must be locally compact.
$\mathcal{C}\mathcal{R}$-epic first countable spaces must be locally compact.
However, a “bad” class of absolute 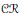 $\mathcal{C}\mathcal{R}$-epic spaces is exhibited whose pathology settles, in the negative, a number of open questions. Spaces which are not absolute
$\mathcal{C}\mathcal{R}$-epic spaces is exhibited whose pathology settles, in the negative, a number of open questions. Spaces which are not absolute 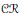 $\mathcal{C}\mathcal{R}$-epic abound, and some are presented.
$\mathcal{C}\mathcal{R}$-epic abound, and some are presented.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2005
References
- 1
- Cited by


