Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Förster, Karl -Heinz
1969.
Über den Abschluß einiger Operatorenalgebren.
Archiv der Mathematik,
Vol. 20,
Issue. 2,
p.
155.
Crabb, M. J.
1970.
Numerical range estimates for the norms of iterated operators.
Glasgow Mathematical Journal,
Vol. 11,
Issue. 2,
p.
85.
Lay, David C.
1970.
Spectral analysis using ascent, descent, nullity and defect.
Mathematische Annalen,
Vol. 184,
Issue. 3,
p.
197.
Taylor, Angus E.
1971.
Notes on the History of the Uses of Analyticity in Operator Theory.
The American Mathematical Monthly,
Vol. 78,
Issue. 4,
p.
331.
Wacker, Hans -Dieter
1986.
Formeln f�r Pole der Resolvente und den Radius eines wesentlichen Spektrums.
Manuscripta Mathematica,
Vol. 54,
Issue. 3,
p.
249.

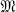 of
of 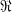 ⊆
⊆ 