Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Foguel, Tuval
and
Kappe, Luise-Charlotte
2005.
On loops covered by subloops.
Expositiones Mathematicae,
Vol. 23,
Issue. 3,
p.
255.
Müller-Hoissen, Folkert
and
Walther, Hans-Otto
2012.
Associahedra, Tamari Lattices and Related Structures.
Vol. 299,
Issue. ,
p.
1.


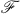 is a quotient group of a group
is a quotient group of a group 