Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-10T23:31:22.233Z Has data issue: false hasContentIssue false
  • English
  • Français

On n-Dimensional Steinberg Symbols

Published online by Cambridge University Press:  20 November 2018

Fernando Pablos Romo
Fernando Pablos Romo*
Affiliation:
Departamento deMatemáticas, Universidad de Salamanca, Plaza de laMerced 1-4, 37008 Salamanca, España e-mail:fpablos@usal.es
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The aim of this work is to provide a new approach for constructing $n$-dimensional Steinberg symbols on discrete valuation fields from 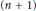$\left( n\,+\,1 \right)$-cocycles and to study reciprocity laws on curves related to these symbols.

Keywords

Primary: 19F15secondary: 19D4519C09Steinberg symbolsreciprocity lawsdiscrete valuation fieldalgebraic curves
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 6 , 01 December 2008 , pp. 1387 - 1405
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Arbarello, E., de Concini, C., and Kac, V. G., The infinite wedge representation and the reciprocity law for algebraic curves. Proc. of Sympos. Pure Math, 1989, 49, Part 1, 171–190.Google Scholar
[2] Brylinsky, J. L. and McLaughlin, D. A., Multidimensional reciprocity laws. J. Reine Angew. Math. 481(1996), 125–147.Google Scholar
[3] Brylinsky, J. L. and McLaughlin, D. A., The geometry of two-dimensional symbols . K-Theory 10(1996), no. 3, 215–237.Google Scholar
[4] Fesenko, I. B., A generalized symbol in multidimensional local fields. In: Rings and modules. Limit theorems of probability theory, 2, (Russian), Leningrad. Univ., 214(1988), 88–92.Google Scholar
[5] Fesenko, I. B. and Vostokov, S., On torsion in higherMilnor functors for multidimensional local fields. Amer. Math. Soc. Transl. 2, 154(1992), 25–35.Google Scholar
[6] Eilenberg, S. and McLane, S., Cohomology theory in abstract groups. I. Ann. Math. 48(1947), 51–78.Google Scholar
[7] Milnor, J., Introduction to algebraic K-theory, Annals of Mathematics Studies 72, Princeton University Press, Princeton, N.J., University of Tokyo Press, Tokyo, 1971.Google Scholar
[8] Pablos Romo, F., 3-Cocycles, symbols and reciprocity laws on curves. J. Pure Appl. Algebra 205(2006), no. 1, 94–116.Google Scholar
[9] Pablos Romo, F., A note on Steinberg symbols on algebraic curves. Comm. Algebra 31(2003), no.2, 981–990.Google Scholar
[10] Pablos Romo, F., Algebraic construction of the tame symbol and the Parshin symbol on a surface. J. Algebra 274(2004), no. 1, 335–346.Google Scholar
[11] Pablos Romo, F., On the tame symbol of an algebraic curve. Comm. Algebra 30(2002), no. 9, 4349–4368.Google Scholar
[12] N.Parshin, A., Local class field theory. Proc. Steklov Inst. Math. 3(1985), 157–185.Google Scholar
[13] N.Parshin, A., Galois cohomology and the Brauer group of local fields. Proc. Steklov Inst. Math., 4(1991), 191–201.Google Scholar
[14] Parshin, A. N. and Shafarevich, I. R., Number Theory II, In: Encyclopaedia of Mathematical Sciences, 62, Springer-Verlag, Berlin, 1992.Google Scholar
[15] Schmidt, H. L., Über das Reziprozitätsgesatz in relativ-zyklischen algebraischen Funktionkörpern mit endlichem Konstantenkörper. Math. Z. 40(1936), 94–109.Google Scholar
[16] Serre, J. P., Groupes algébriques et corps de classes, Publications de l’institut de mathématique de l’université de Nancago, VII, Hermann, Paris, 1959.Google Scholar
[17] Tate, J., Residues of differentials on curves. Ann. Scient.Éc. Norm. Sup.(4) 1(1968), 149–159.Google Scholar