Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T19:36:21.798Z Has data issue: false hasContentIssue false
  • English
  • Français

On Nonabelian H2 for Profinite Groups

Published online by Cambridge University Press:  20 November 2018

K.-H. Ulbrich
K.-H. Ulbrich*
Affiliation:
Département de Mathématiques UniversitéParis-Nord 93430 Villetaneuse, France
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a profinite group. We define an extension (E, J) of G by a group A to consist of an exact sequence of groups 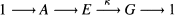together with a section j : G → E of K satisfying: 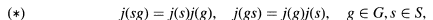for some open normal subgroup Sof G, and the map 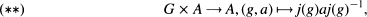is continuous (A being discrete).

Keywords

20J05
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 44 , Issue 2 , 01 April 1992 , pp. 388 - 399
Copyright
Copyright © Canadian Mathematical Society 1992

References

1. Eilenberg, S. and Mac, S. Lane, Cohomology theory in abstract groups, II, Ann. Math. 48(1947), 326–341.Google Scholar
2. Giraud, J., Cohomologie non abélienne, Grundl. math. Wiss. 179(Springer-Verlag, Berlin 1972).Google Scholar
3. Langlands, R.P. und Rapoport, M., Shimuravarietäten und Gerben, J. reine angew. Math. 378(1987), 113- 220.Google Scholar
4. Serre, J.-R, Cohomologie Galoisienne, Lect. Notes Math. 5(Springer-Verlag, Berlin 1965).Google Scholar
5. Shatz, S., Profinite groups, Arithmetic and Geometry, Annals Math. Studies 67(Princeton 1972).Google Scholar
6. Springer, T.A., Nonabelian H2 in Galois cohomology, Proc. Symp. Pure Math. 9(1966), 164–182.Google Scholar