Hostname: page-component-66644f4456-srn29 Total loading time: 0 Render date: 2025-02-12T19:33:28.950Z Has data issue: true hasContentIssue false
  • English
  • Français

On Operator Algebras and Invariant Subspaces

Published online by Cambridge University Press:  20 November 2018

Chandler Davis ,
Heydar Radjavi  and
Peter Rosenthal
Chandler Davis
Affiliation:
University of Toronto, Toronto, Ontario
Heydar Radjavi
Affiliation:
University of Toronto, Toronto, Ontario
Peter Rosenthal
Affiliation:
University of Toronto, Toronto, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If 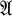is a collection of operators on the complex Hilbert space 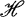, then the lattice of all subspaces of 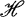which are invariant under every operator in 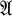is denoted by Lat 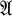. An algebra 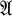of operators on 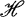is defined (3; 4) to be reflexive if for every operator B on 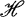the inclusion Lat 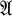⊆ Lat B implies .

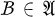Arveson (1) has proved the following theorem. (The abbreviation “m.a.s.a.” stands for “maximal abelian self-adjoint algebra”.)

ARVESON's THEOREM. If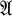is a weakly closed algebra which contains an m.a.s.a.y and if Lat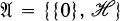, then 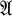is the algebra of all operators on .

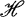A generalization of Arveson's Theorem was given in (3). Another generalization is Theorem 2 below, an equivalent form of which is Corollary 3. This theorem was motivated by the following very elementary proof of a special case of Arveson's Theorem.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 1178 - 1181
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Arveson, W. B., A density theorem for operator algebras, Duke Math. J. 34 (1967), 635–647.Google Scholar
2. Jacobson, N., Lectures in abstract algebra, Vol. 2 (Van Nostrand, Princeton, N.J., 1953).Google Scholar
3. Radjavi, H. and Rosenthal, P., Invariant subspaces and weakly closed algebras, Bull. Amer. Math. Soc. 74 (1968), 1013–1014.Google Scholar
4. Radjavi, H. and Rosenthal, P., On invariant subspaces and reflexive algebras (to appear in Amer. J. Math.).Google Scholar