Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-16T00:51:19.311Z Has data issue: false hasContentIssue false
  • English
  • Français

On Partially Ordering Operator Algebras

Published online by Cambridge University Press:  20 November 2018

Ralph Demarr
Ralph Demarr*
Affiliation:
University of Washington
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we consider linear spaces and algebras with real scalars. It is well known that if X is a Banach space and 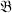is the set of all bounded linear operators which map X into itself, then 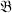is a Banach algebra. In this paper we shall show that 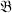can be partially ordered so that it becomes a partially ordered algebra in which norm convergence is equivalent to order convergence. This motivates a study of Banach algebras of operators in which one uses the order structure to obtain various results. In addition, it encourages a study of partially ordered algebras in general, since our result shows that among such algebras one finds all real Banach algebras of operators. Of course, there are many other real algebras which are naturally partially ordered and which have been studied from that point of view.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 19 , 1967 , pp. 636 - 643
Copyright
Copyright © Canadian Mathematical Society 1967

References

1. Birkhoff, G., Lattice theory, Amer. Math. Soc., Colloquium Publications, vol. 25, rev. ed. (1948).Google Scholar
2. DeMarr, R. E., Order convergence in linear topological spaces, Pacific J. Math., 14 (1964), 17–20.Google Scholar
3. DeMarr, R. E., Partially ordered linear spaces and locally convex linear topological spaces, Illinois J. Math., 8 (1964), 601–606.Google Scholar
4. Kadison, R. V., A representation theory for commutative topological algebras, Mem. Amer. Math. Soc., No. 7 (1951).Google Scholar
5. Kantorovich, L. V., Pinsker, A. G., and Vulikh, B. Z., Functional analysis in semi-ordered spaces (Moscow-Leningrad, 1950).Google Scholar
6. McShane, E. J., Order-preserving maps and integration processes, Ann. of Math. Studies, No. 31 (1953).Google Scholar
7. Nakano, H., Modern spectral theory (Tokyo, 1950).Google Scholar
8. Namioka, I., Partially ordered linear topological spaces, Mem. Amer. Math. Soc., No. 24 (1957).Google Scholar
9. Vulikh, B. Z., Introduction to the theory of semi-ordered spaces (in Russian; Moscow, 1961).Google Scholar