Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T00:15:12.676Z Has data issue: false hasContentIssue false
  • English
  • Français

On Partitions into Powers of Primes and Their Difference Functions

Published online by Cambridge University Press:  20 November 2018

Roger Woodford
Roger Woodford*
Affiliation:
Department of Mathematics, The University of British Columbia, Vancouver, B.C., Canada V6T 1Z2, roger.dmw@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

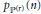In this paper, we extend the approach first outlined by Hardy and Ramanujan for calculating the asymptotic formulae for the number of partitions into $r$-th powers of primes, ${{p}_{\mathbb{P}\left( r \right)}}\left( n \right)$, to include their difference functions. In doing so, we rectify an oversight of said authors, namely that the first difference function is perforce positive for all values of $n$, and include the magnitude of the error term.

Keywords

05A1711P81
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 2 , 01 April 2009 , pp. 465 - 480
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Bateman, P. T. and Erdös, P., Partitions into primes. Publ. Math. Debrecen 4(1956), 198–200.Google Scholar
[2] Bateman, P. T. and Erdös, P., Monotonicity of partition functions. Mathematika 3(1956), 1–14.Google Scholar
[3] Grosswald, E., Partitions into prime powers. Michigan Math. J. 7(1960), 97–122.Google Scholar
[4] Gupta, H., Products of parts in partitions into primes. Res. Bull. Panjab. Univ. (N. S.) 21(1970), 251–253.Google Scholar
[5] Hardy, G. H. and Ramanujan, S., Asymptotic formulae for the distribution of integers of various types. Proc. London Math. Soc. (2) 16(1917), 112–132.Google Scholar
[6] Kerawala, S. M., On the asymptotic values of ln p A (n ) and ln p (d ) A (n ) with A as the set of primes. J. Natur. Sci. and Math. 9(1969), 209–216.Google Scholar
[7] Mitsui, T., On the partitions of a number into the powers of prime numbers. J. Math. Soc. Japan 9(1957), 428–447.Google Scholar