Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T15:02:52.076Z Has data issue: false hasContentIssue false
  • English
  • Français

On Some Generalized Rapoport–Zink Spaces

Part of: Arithmetic problems. Diophantine geometry Arithmetic algebraic geometry

Published online by Cambridge University Press:  03 May 2019

Xu Shen
Xu Shen*
Affiliation:
Morningside Center of Mathematics, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, No. 55, Zhongguancun East Road, Beijing 100190, China Email: shen@math.ac.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

We enlarge the class of Rapoport–Zink spaces of Hodge type by modifying the centers of the associated 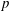$p$-adic reductive groups. Such obtained Rapoport–Zink spaces are said to be of abelian type. The class of Rapoport–Zink spaces of abelian type is strictly larger than the class of Rapoport–Zink spaces of Hodge type, but the two type spaces are closely related as having isomorphic connected components. The rigid analytic generic fibers of Rapoport–Zink spaces of abelian type can be viewed as moduli spaces of local 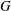$G$-shtukas in mixed characteristic in the sense of Scholze.

We prove that Shimura varieties of abelian type can be uniformized by the associated Rapoport–Zink spaces of abelian type. We construct and study the Ekedahl–Oort stratifications for the special fibers of Rapoport–Zink spaces of abelian type. As an application, we deduce a Rapoport–Zink type uniformization for the supersingular locus of the moduli space of polarized K3 surfaces in mixed characteristic. Moreover, we show that the Artin invariants of supersingular K3 surfaces are related to some purely local invariants.

Keywords

Rapoport–Zink spaceshtukaShimura varietyK3 surface

MSC classification

Primary: 11G18: Arithmetic aspects of modular and Shimura varieties
Secondary: 14G35: Modular and Shimura varieties
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 5 , October 2020 , pp. 1111 - 1187
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was partially supported by the Chinese Academy of Sciences grants 50Y64198900, 29Y64200900, the Recruitment Program of Global Experts of China, and the NSFC grants No. 11631009 and No. 11688101.

References

Bhatt, B. and Scholze, P., Projectivity of the Witt vector affine Grassmannian. Invent. Math. 209(2017), no. 2, 329–423. https://doi.org/10.1007/s00222-016-0710-4Google Scholar
Borovoi, M., Abelian Galois cohomology of reductive groups. Mem. Amer. Math. Soc. 132(1998), no. 626, 1–50. https://doi.org/10.1090/memo/0626Google Scholar
Boutot, J.-F. and Zink, T., The p-adic uniformization of Shimura curves, Preprint, available at https://www.math.uni-bielefeld.de/∼zink/p-adicuni.psGoogle Scholar
Bültel, O. and Pappas, G., (G, 𝜇)-displays and Rapoport–Zink spaces. J. Inst. Math. Jussieu, to appear. arxiv:1702.00291Google Scholar
Caraiani, A. and Scholze, P., On the generic part of the cohomology of compact unitary Shimura varieties. Ann. of Math. 186(2017), no. 3, 649–766. https://doi.org/10.4007/annals.2017.186.3.1Google Scholar
Chen, M., Composantes connexes géométriques d’espaces de modules de groupes p-divisibles. Ann. Sci. Éc. Norm. Sup. 47(2014), 723–764. https://doi.org/10.24033/asens.2225Google Scholar
Chen, M., Kisin, M., and Viehmann, E., Connected components of affine Deligne–Lusztig varieties in mixed characteristic. Compositio. Math. 151(2015), 1697–1762. https://doi.org/10.1112/S0010437X15007253Google Scholar
Chen, M., Kisin, M., and Viehmann, E., Corrigendum Connected components of affine Deligne–Lusztig varieties in mixed characteristic. Compositio. Math. 153(2017), 218–222. https://doi.org/10.1112/S0010437X1600782XGoogle Scholar
Chen, M., Fargues, L., and Shen, X., On the structure of some p-adic period domains. arxiv:1710.06935Google Scholar
Dat, J.-F., Orlik, S., and Rapoport, M., Period domains over finite and p-adic fields. Cambridge Tracts in Mathematics, 183, Cambridge University Press, Cambridge, 2010. https://doi.org/10.1017/CBO9780511762482Google Scholar
Deligne, P., Variétés de Shimura: interprétation modulaire, et techniques de construction de modèles canoniques. In: Automorphic forms, representations and L-functions (Corvallis 1977). Proc. Sympos. Pure Math., XXXIII, Amer. Math. Soc., Providence, RI, 1979, pp. 247–289.Google Scholar
Drinfeld, V. G., Coverings of p-adic symmetric regions. Funkcional Anal. i Prilozen 10(1976), 29–40.Google Scholar
Ekedahl, T. and van der Geer, G., Cycle classes on the moduli of K3 surfaces in positive characteristic. Selecta Math. (N. S.) 21(2015), no. 1, 245–291. https://doi.org/10.1007/s00029-014-0156-8Google Scholar
Faltings, G., Coverings of p-adic period domains. J. Reine Angew. Math. 643(2010), 111–139. https://doi.org/10.1515/CRELLE.2010.046Google Scholar
Fargues, L., Geometrization of the local Langlands correspondence: an overview. arxiv:1602.00999Google Scholar
Fargues, L., Quelques résultats et conjectures concernant la courbe. In: De la géométrie algébrique aux formes automorphes (I) - (Une collection d’articles en l’honneur du soixantième anniversaire de Gérard Laumon). Astérisque, 369, 2015.Google Scholar
Fargues, L., G-torseurs en théorie de Hodge p-adique. Compositio Math., to appear.Google Scholar
Fargues, L., Lettre à Rapoport. https://webusers.imj-prg.fr/∼laurent.fargues/index.htmlGoogle Scholar
Fargues, L., p-adic Twistors and Shtukas, Lecture notes. https://webusers.imj-prg.fr/∼laurent.fargues/Notes.htmlGoogle Scholar
Fargues, L. and Fontaine, J.-M., Courbes et fibrés vectoriels en théorie de Hodge p-adique. Astérisque, 406, Soc. Math. France, 2018.Google Scholar
Görtz, U. and He, X., Basic loci in Shimura varieties of coxeter type. Camb. J. Math. 3(2015), 323–353. https://doi.org/10.4310/CJM.2015.v3.n3.a2Google Scholar
Görtz, U., He, X., and Nie, S., Fully Hodge–Newton decomposable Shimura varieties. arxiv:1610.05381Google Scholar
Grothendieck, A., Éléments de géométrie algébrique (rédigés avec la collaboration de Jean Dieudonné): I. Étude locale des schémas et de morphismes de schémas, Première partie. Inst. Hautes Études Publ. Math. 20(1964), 5–259.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique (rédigés avec la collaboration de Jean Dieudonné): IV. Étude locale des schémas et de morphismes de schémas, Quatrième partie. Inst. Hautes Études Publ. Math. 32(1967), 5–361.Google Scholar
Hamacher, P., On the Newton stratification in the good reduction of Shimura varieties. J. Algebraic. Geom., to appear. arxiv:1605.05540Google Scholar
Hansen, D., Period morphisms and variation of p-adic Hodge structure (preliminary draft). http://www.math.columbia.edu/∼hansen/periodmapmod.pdfGoogle Scholar
Hartl, U., On a conjecture of Rapoport and Zink. Invent. Math. 195(2013), 627–696. https://doi.org/10.1007/s00222-012-0437-9Google Scholar
Hartl, U. and Viehmann, E., The generic fiber of moduli spaces of bounded local G-shtukas. arxiv:1712.07936Google Scholar
He, X., Geometric and homological properties of affine Deligne–Lusztig varieties. Ann. of Math. 179(2014), 367–404. https://doi.org/10.4007/annals.2014.179.1.6Google Scholar
He, X. and Rapoport, M., Stratifications in the reduction of Shimura varieties. Manuscripta Math. 152(2017), no. 3–4, 317–343. https://doi.org/10.1007/s00229-016-0863-xGoogle Scholar
He, X. and Zhou, R., On the connected components of affine Deligne–Lusztig varieties. arxiv:1610.06879Google Scholar
Howard, B. and Pappas, G., Rapoport–Zink spaces for spinor groups. Compos. Math. 153(2017), no. 5, 1050–1118. https://doi.org/10.1112/S0010437X17007011Google Scholar
de Jong, A. J., Étale fundamental groups of non-Archimedean analytic spaces. Compositio Math. 97(1995), 89–118.Google Scholar
de Jong, A. J., Crystalline Dieudonné module theory via formal and rigid geometry. Inst. Hautes Études Sci. Publ. Math. 82(1995), 5–96.Google Scholar
Kedlaya, K. S. and Liu, R., Relative p-adic Hodge theory: foundations. Astérisque, 371, Soc. Math. France, 2015.Google Scholar
Kim, W., Rapoport–Zink spaces of Hodge type. Forum Math. Sigma 6(2018), e8, 110 pp. https://doi.org/10.1017/fms.2018.6Google Scholar
Kim, W., Rapoport–Zink uniformization of Hodge type Shimura varieties. Forum Math. Sigma 6(2018), e16, 36 pp. https://doi.org/10.1017/fms.2018.18Google Scholar
Kisin, M., Integral models for Shimura varieties of abelian type. J. Amer. Math. Soc. 23(2010), 967–1012. https://doi.org/10.1090/S0894-0347-10-00667-3Google Scholar
Kisin, M., Mod p points on Shimura varieties of abelian type. J. Amer. Math. Soc. 30(2017), 819–914. https://doi.org/10.1090/jams/867Google Scholar
Kottwitz, R. E., Isocrystals with additional structure. Compositio Math. 56(1985), 201–220.Google Scholar
Kottwitz, R. E., Isocrystals with additional structure. II. Compositio Math. 109(1997), 255–339. https://doi.org/10.1023/A:1000102604688Google Scholar
Lafforgue, V., Introduction aux chtoucas pour les groupes réductifs et à la paramétrisation de Langlands globale. J. Amer. Math. Soc. 31(2018), 719–891. https://doi.org/10.1090/jams/897Google Scholar
Lau, E., Displays and formal p-divisible groups. Invent. Math. 171(2008), no. 3, 617–628. https://doi.org/10.1007/s00222-007-0090-xGoogle Scholar
Li, C. and Zhu, Y., Arithmetic intersection on GSpin Rapoport–Zink spaces. Compositio Math. 154(2018), no. 7, 1407–1440. https://doi.org/10.1112/S0010437X18007108Google Scholar
Liedtke, C., Supersingular K3 surfaces are unifrational. Invent. Math. 200(2015), no. 3, 979–1014. https://doi.org/10.1007/s00222-014-0547-7Google Scholar
Liu, R. and Zhu, X., Rigidity and a Riemann–Hilbert correspondence for p-adic local systems. Invent. Math. 207(2017), no. 1, 291–343. https://doi.org/10.1007/s00222-016-0671-7Google Scholar
Madapusi Pera, K., The Tate conjecture for K3 surfaces in odd characteristic. Invent. Math. 201(2015), 625–668. https://doi.org/10.1007/s00222-014-0557-5Google Scholar
Matsumura, H., Commutative algebra, Second ed., Mathematics Lecture Note Series, 56, Benjamin/Cummings Publishing Co., Inc., Reading, MA, 1980.Google Scholar
Nie, S., Connected components of closed affine Deligne–Lusztig varieties in affine Grassmannians. Amer. J. Math. 140(2018), no. 5, 1357–1397. https://doi.org/10.1353/ajm.2018.0034Google Scholar
Ogus, A., Singularities of the height strata in the moduli of K3 surfaces. In: Moduli of abelian varieties (Texel Island, 1999). Progr. Math., 195, Birkhäuser, Basel, 2001, pp. 325–343.Google Scholar
Pink, R., Wedhorn, T., and Ziegler, P., F-zips with additional structure. Pacific J. Math. 274(2015), no. 1, 183–236. https://doi.org/10.2140/pjm.2015.274.183Google Scholar
Rapoport, M., Non-archimedean period domains. In: Proceedings of the International Congress of Mathematicians, vol. 1, 2 (Zürich, 1994). Birkhäuser, Basel, 1995, pp. 423–434.Google Scholar
Rapoport, M., A guide to the reduction modulo p of Shimura varieties. Automorphic forms. I. Astérisque 298(2005), 271–318.Google Scholar
Rapoport, M., Accessible and weakly accessible period domains. Appendix of P. Scholze, On the p-adic cohomology of the Lubin–Tate tower. Ann. Sci. École Norm. Sup. 51(2018), no. 4, 856–863. https://doi.org/10.24033/asens.2367Google Scholar
Rapoport, M. and Richartz, M., On the classification and specialization of F-isocrystals with additional structure. Compositio Math. 103(1996), no. 2, 153–181.Google Scholar
Rapoport, M. and Zink, T., Period spaces for p-divisible groups. Ann. of Math. Stud., 141, Princeton University Press, Princeton, NJ, 1996.Google Scholar
Rapoport, M. and Viehmann, E., Towards a theory of local Shimura varieties. Münster J. Math. 7(2014), 273–326.Google Scholar
Rizov, J., Moduli stacks of polarized K3 surfaces in mixed characteristic. Serdica Math. J. 32(2006), no. 2–3, 131–178.Google Scholar
Rizov, J., Kuga–Satake abelian varieties of K3 surfaces in mixed characteristic. J. Reine Angew. Math. 648(2010), 13–67. https://doi.org/10.1515/CRELLE.2010.078Google Scholar
Scholze, P., Perfectoid spaces. Publ. Math. Inst. Hautes Études Sci. 116(2012), no. 1, 245–313. https://doi.org/10.1007/s10240-012-0042-xGoogle Scholar
Scholze, P., Lectures on p-adic geometry. Notes taken by J. Weinstein, Fall 2014. http://math.bu.edu/people/jsweinst/Math274/ScholzeLectures.pdfGoogle Scholar
Scholze, P., Étale cohomology of diamonds. arxiv:1709.07343Google Scholar
Scholze, P., p-adic geometry. Proceedings of the ICM 2018.Google Scholar
Scholze, P. and Weinstein, J., Berkeley lectures on p-adic geometry. http://www.math.uni-bonn.de/people/scholze/Berkeley.pdfGoogle Scholar
Scholze, P. and Weinstein, J., Moduli of p-divisible groups. Cambridge J. Math. 1(2013), 145–237. https://doi.org/10.4310/CJM.2013.v1.n2.a1Google Scholar
Serre, J.-P., Groupes algébriques associés aux modules de Hodge–Tate. In: Journées de Géométrie Algébrique de Rennes (Rennes 1978), Vol. III. Astérisque, 65, Soc. Math. France, Paris, 1979, pp. 155–188.Google Scholar
Shen, X., Perfectoid Shimura varieties of abelian type. Int. Math. Res. Not. IMRN 2017 no. 21, 6599–6653. https://doi.org/10.1093/imrn/rnw202Google Scholar
Shen, X. and Zhang, C., Stratifications in good reductions of Shimura varieties of abelian type. arxiv:1707.00439Google Scholar
Vollaard, I. and Wedhorn, T., The supersingular locus of the Shimura variety of GU (1, n - 1). II. Invent. Math. 184(2011), 591–627. https://doi.org/10.1007/s00222-010-0299-yGoogle Scholar
Varshavsky, Y., Moduli spaces of principal F-bundles. Selecta Math. (N.S.) 10(2004), no. 1, 131–166. https://doi.org/10.1007/s00029-004-0343-0Google Scholar
Viehmann, E., Truncations of level 1 of elements in the loop group of a reductive group. Ann. of Math. (2) 179(2014), 1009–1040. https://doi.org/10.4007/annals.2014.179.3.3Google Scholar
Wedhorn, T., Ekedahl–Oort strata of Shimura varieties. Lecture notes in a Summer School on Shimura varieties, 2016, NCTS, Taiwan.Google Scholar
Wintenberger, J.-P., Existence de F-cristaux avec structures supplémentaires. Adv. Math. 190(2005), 196–224. https://doi.org/10.1016/j.aim.2003.12.006Google Scholar
Wortmann, D., The 𝜇-ordinary locus for Shimura varieties of Hodge type. arxiv:1310.6444Google Scholar
Xiao, L. and Zhu, X., Cycles on Shimura varieties via geometric Satake. arxiv:1707.05700Google Scholar
Yang, Z., Isogenies between K3 surfaces over 𝔽p. arxiv:1810.08546Google Scholar
Zhang, C., Ekedahl–Oort strata for good reductions of Shimura varieties of Hodge type. Canad. J. Math. 70(2018), no. 2, 451–480. https://doi.org/10.4153/CJM-2017-020-5Google Scholar
Zhu, X., Affine Grassmannians and the geometric Satake in mixed characteristic. Ann. of Math. 185(2017), no. 2, 403–492. https://doi.org/10.4007/annals.2017.185.2.2Google Scholar
Zink, T., The display of a formal p-divisible group. Cohomologies p-adiques et applications arithmétiques, I. Astérisque 278(2002), 127–248.Google Scholar