On some multiplicative properties of large difference sets

Abstract

In our paper, we study multiplicative properties of difference sets $A-A$ for large sets 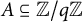$A \subseteq {\mathbb {Z}}/q{\mathbb {Z}}$ in the case of composite q. We obtain a quantitative version of a result of A. Fish about the structure of the product sets 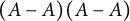$(A-A)(A-A)$. Also, we show that the multiplicative covering number of any difference set is always small.

1 Introduction

The landmark question about solvability of equations of the form $f(x_1,\dots ,x_n) = 0$ , where $f\in {\mathbb {Z}}[x_1,\dots ,x_n]$ and the variables $x_j \in X_j$ belong to some “large” but unspecified sets $X_j$ of the prime field $\mathbb {F}_q$ was firstly posed, probably, in [12]. Interesting in its own right, the problem has a clear connection with the sum–product phenomenon [21] due to the fact that as a rule the polynomial f includes both the addition and the multiplication. This theme becomes rather popular last years (see, e.g., [7–10, 12, 16, 19] and many other papers).

The question about a partial resolution of some specific equations $f(x_1,\dots ,x_n)=0$ in large subrings of rings ${\mathbb {Z}}_q := {\mathbb {Z}}/(q {\mathbb {Z}})$ for composite q was firstly considered by Fish in [5] (nevertheless, let us remark that a similar problem was formulated in [8, Problem 5]). In particular, in [5, Corollary 1.2], Fish considered the polynomial $f(x_1,x_2,x_3,x_4) = (x_1-x_2)(x_3-x_4)$ and proved the following result.

Theorem 1.1 [Fish]

Let q be a positive integer, let $A, B\subset {\mathbb {Z}}_q$ be sets, $|A| = \alpha q$ , $|B|=\beta q$ , and suppose that $\alpha \geqslant \beta $ . Then there is $d|q$ with

(1.1) $$ \begin{align} d \leqslant F(\beta) := \exp \exp \exp( C\beta^{-4}) , \end{align} $$

where $C>0$ is an absolute constant and such that

(1.2) $$ \begin{align} d \cdot {\mathbb{Z}}_q \subseteq (A-A)(B-B) . \end{align} $$

Here, we use the following standard notation [21], namely, given two sets $A,B\subset {\mathbb {Z}}_q$ , define the sumset of A and B as

$$ \begin{align*}A+B:=\{a+b ~:~ a\in{A},\,b\in{B}\}.\end{align*} $$

In a similar way, we define the difference sets $A-A$ , the higher sumsets, e.g., $2A-A$ is $A+A-A$ and, further, the products sets

$$ \begin{align*}AB:=\{ab ~:~ a\in{A},\,b\in{B}\}\end{align*} $$

the higher product sets and so on. Finally, if $A \subseteq {\mathbb {Z}}_q$ and $\lambda \in {\mathbb {Z}}_q$ , then we write

$$\begin{align*}\lambda \cdot A = \{ \lambda a ~:~ a\in A\} . \end{align*}$$

It is easy to see that in this generality one cannot have ${\mathbb {Z}}_q = (A-A)(B-B)$ in inclusion (1.2) for all sets $A,B,$ and thus, we indeed need this additional (but small) divisor d. In contrary, for prime $q,$ the divisor d can be omitted and the questions of this type were studied in [9] and [19]. As we have seen the dependence in $F(\beta )$ was triple exponential on $\beta ^{-1}$ . Using a series of other methods, we improve and generalize the last result in several directions. The signs $\ll $ and $\gg $ below are the usual Vinogradov symbols.

Theorem 1.2 Let q be a positive integer, let $A, B\subset {\mathbb {Z}}_q$ be sets, $|A| = \alpha q$ , $|B|=\beta q$ , and suppose that $\alpha \geqslant \beta $ . Then there is $d|q$ with

(1.3) $$ \begin{align} d \ll \exp( C\beta^{-4}) , \end{align} $$

where $C>0$ is an absolute constant and such that

(1.4) $$ \begin{align} d \cdot {\mathbb{Z}}_q \subseteq (A-A)(B-B) . \end{align} $$

In [5], the author posed a series of questions in much more general form, as well as for other polynomials $f(x_1,\dots ,x_n)$ . Using different approaches, we partially resolve some of them (see Sections 3 and 4). In particular, we have deal with the equation

$$\begin{align*}(a_1-b_1) (a_2 - b_2) \equiv \lambda\quad \pmod q \,, \quad \quad (a_1,a_2) \in \mathcal{A},\, (b_1,b_2) \in \mathcal{B} , \end{align*}$$

and

$$\begin{align*}(a_1-b_1)^2 - (a_2 - b_2)^2 \equiv \lambda\quad \pmod q \,, \quad \quad (a_1,a_2) \in \mathcal{A},\, (b_1,b_2) \in \mathcal{B,} \end{align*}$$

for rather general two-dimensional sets $\mathcal {A}, \mathcal {B} \subseteq {\mathbb {Z}}_q \times {\mathbb {Z}}_q$ and composite numbers q with some restrictions on its prime divisors (see Theorems 3.2, 3.5, and 4.1). As an example, we formulate a part of Theorem 3.2. Giving a positive integer $q,$ we denote by $\omega (q)$ the total number of prime divisors of q.

Theorem 1.3 Let q be a squarefree number, let $\mathcal {A}, \mathcal {B} \subseteq {\mathbb {Z}}_q^2$ be sets, $|\mathcal {A}| = \alpha q^2$ , $|\mathcal {B}|=\beta q^2$ , and suppose that $\alpha \geqslant \beta $ . Then

(1.5) $$ \begin{align} d \cdot {\mathbb{Z}}^*_q \subseteq \{ (a_1-b_1) (a_2 - b_2) ~:~ (a_1,a_2) \in \mathcal{A},\, (b_1,b_2) \in \mathcal{B} \} \end{align} $$

with

$$\begin{align*}d \ll \exp (O(\omega(q) \log \omega(q) - \log \beta)) . \end{align*}$$

In particular, for $\mathcal {A} = \mathcal {B}$ , one has with the same d that

(1.6) $$ \begin{align} d \cdot {\mathbb{Z}}_q \subseteq \{ (a_1-b_1) (a_2 - b_2) ~:~ (a_1,a_2) \in \mathcal{A},\, (b_1,b_2) \in \mathcal{B} \} . \end{align} $$

Our another result may be interesting in itself (even in the case of prime q) due to it gives a new necessary condition for a set to be a difference set, but moreover, in addition, it yields another proof of Theorem 1.1 (see Theorems 5.4 and 5.9).

Theorem 1.4 Let q be a positive integer, and let $A \subseteq {\mathbb {Z}}_q$ be a set, $|A| = \alpha q$ . Suppose that the least prime factor of q greater than $2 \alpha ^{-1}+3$ . Then, there is $X \subseteq {\mathbb {Z}}_q$ such that

$$ \begin{align*} |X| \leqslant \frac{1}{\alpha} + 1 , \end{align*} $$

and

$$\begin{align*}X(A-A) = {\mathbb{Z}}_q . \end{align*}$$

The equation $X(A-A) = {\mathbb {Z}}_q$ for a set $X \subseteq {\mathbb {Z}}_q$ induces a coloring of ${\mathbb {Z}}_q$ via suitable subsets of our difference set $A-A$ . Hence, Theorem 1.4 gives us a new connection between coloring problems and difference sets. Finally, our result and the Ruzsa covering lemma [11] (see inclusion (5.2)) show that for any set $A\subseteq {\mathbb {Z}}_q$ , $|A| \gg q$ , where q is a prime number, say, the set $A-A$ is a syndetic set (i.e., having bounded gaps between its consecutive elements, e.g., see [6]) in both multiplicative and additive ways.

Let us say a few words about the notation. Having a positive integer q, we denote by $\omega (q)$ the total number of prime divisors of q and by $\tau (q)$ the number of all divisors. Let $\varphi (q)$ be the Euler function. We use the same capital letter to denote a set $A\subseteq {\mathbb {Z}}_q$ and its characteristic function $A: {\mathbb {Z}}_q \to \{0,1 \}$ . If $\mathcal {R}$ is a ring, then we write $\mathcal {R}^*$ for the group of all inverse elements of $\mathcal {R}$ . Let $e_q(x) = e^{2\pi i x/q}$ , and let us denote by $[n]$ the set $\{1,2,\dots , n\}$ . All logarithms are to base $2$ .

2 An effective version of Fish’s theorem

Having a positive integer n and a set $A \subseteq {\mathbb {Z}}_q \times \dots \times {\mathbb {Z}}_q = {\mathbb {Z}}^n_q$ (or just $A\subset {\mathbb {Z}}^n$ ), as well as a divisor $q_*|q$ , we write

$$ \begin{align*}\pi_{q_*} (A) = \{ (a_1\quad \pmod{q_*},~ \dots ~,~ a_n\quad \pmod{q_*}) ~:~ (a_1,\dots, a_n) \in A \} \subseteq {\mathbb{Z}}^n_{q_*} . \end{align*} $$

We need a regularization result similar to [2, Lemma 2.1].

Lemma 2.1 Let $\delta ,\varepsilon \in (0,1)$ , $M\geqslant 2$ be real numbers, let n be a positive integer, and let $A\subset {\mathbb {Z}}^n_q$ be a set, $|A|=\delta q^n$ . Then, there is $q_*|q$ , and a set $A_* \subseteq A$ , $|\pi _{q/q_*} (A_*)| = 1$ such that $q_* = \frac {q}{q_1 \dots q_s}$ , $M\leqslant q_j \leqslant \delta ^{-\varepsilon ^{-1}}$ , s is the least number with $\delta M^{\varepsilon s}> 1$ and for all $\tilde {q}|q_*$ , $\tilde {q} \geqslant M$ one has

(2.1) $$ \begin{align} \max_{\xi \in {\mathbb{Z}}^n_{\tilde{q}}} |A_* \cap \pi^{-1}_{\tilde{q}} (\xi)| \leqslant \frac{|A_*|}{\tilde{q}^{1-\varepsilon}} . \end{align} $$

Proof Suppose not. Then for a certain $\xi \in {\mathbb {Z}}^n_{q}$ and $q_1|q$ , $q_1 \geqslant M$ , we find ${A' := A \cap \pi ^{-1}_{q_1} (\xi )}$ with $|A'|\geqslant \frac {|A|}{q^{1-\varepsilon }_1}$ . Clearly, $|\pi _{q_1} (A')| = 1$ and the density of $A'$ in the appropriate shift of ${\mathbb {Z}}^n_{q/q_1}$ is at least $\delta q^\varepsilon _1 \geqslant \delta M^{\varepsilon }$ . Hence, applying the same procedure to the set $A'$ and to the new module $q/q_1$ , we see that our algorithm must stop after at most s steps. Notice that condition (2.1) holds automatically if $\tilde {q} \geqslant \delta ^{-\varepsilon ^{-1}}$ , and hence, at the final step of our procedure, we find a set $A_* \subset A$ , $|\pi _{q/q_*} (A_*)| = 1$ , having all required properties. This completes the proof.

Example 2.2 Let $n=1$ and $q=p_1\dots p_s$ , where $p_j$ be some prime numbers. Given a set $A\subset {\mathbb {Z}}_q$ , we are interested in distribution of A among arithmetic progressions of the form $\alpha \tilde {q}+\beta $ , where $\tilde {q}\geqslant M$ is any divisor of q, $\beta $ is a fixed number from the segment $[\tilde {q}]$ and $\alpha $ runs over the segment $[q/\tilde {q}]$ . Of course, not all sets A are uniformly distributed among such progressions, e.g., take $A=A_0=\{0, \tilde {q}, 2 \tilde {q} \dots , L \tilde {q}\}$ , ${L=q/\tilde {q} - 1}$ but nevertheless one can always find a subset $A_*$ of our set such that this new set $A_*$ does not correlate with these arithmetic progressions in the sense of inequality (2.1). In our particular case, just take $A_* = A_0$ and $q_* = q/\tilde {q}$ .

Now, we are ready to obtain the main result of this section, which implies Theorem 1.2 from the introduction. Our proof uses the Fourier analysis (its standard facts can be found in [21], say) and classical estimates for the Kloosterman sums. Having a group ${\mathbf G}$ , we define for any function $f:{\mathbf G} \to \mathbb {C}$ and a representation $\rho \in \widehat {{\mathbf G}}$ the Fourier transform of f at $\rho $ by the formula

(2.2) $$ \begin{align} \widehat{f} (\rho) = \sum_{g\in {\mathbf G}} f(g) \rho (g) . \end{align} $$

Theorem 2.3 Let q be a positive integer, let $A, B\subset {\mathbb {Z}}_q$ be sets, $|A| = \alpha q$ , $|B|=\beta q$ , and suppose that $\alpha \geqslant \beta $ . Then, there is $d|q$ with

(2.3) $$ \begin{align} d \ll \exp( C\beta^{-4}) , \end{align} $$

where $C>0$ is an absolute constant and such that

(2.4) $$ \begin{align} d \cdot {\mathbb{Z}}_q \subseteq (A-A)(B-B) . \end{align} $$

In addition,

(2.5) $$ \begin{align} d \ll \beta^{-O(\omega(q))} . \end{align} $$

Proof Let $q=p_1^{\rho _1} \dots p_t^{\rho _t}$ , where $p_j$ are different primes, $p_1<\dots <p_t$ . Also, let $M\geqslant 2$ , $\varepsilon \in (0,1)$ be parameters, which we will choose later. First of all, we remove all divisors less than M from q. More precisely, for any $p_j$ , $j\in [t]$ let $\gamma _j \leqslant \rho _j$ be the maximal nonnegative integer such that $p^{\gamma _j}_j \leqslant M$ . Clearly, $\gamma _1 \geqslant \gamma _2 \geqslant \dots \gamma _t \geqslant 0$ and let $t_0 \leqslant t$ be the maximal j with $\gamma _j \neq 0$ . Thus $t_0 \leqslant \pi (M)$ . Now, we define

(2.6) $$ \begin{align} Q_1 := \prod_{j=1}^{t_0} p_j^{\gamma_j} \leqslant M^{t_0} \leqslant \min\{ M^{\pi (M)}, M^{\omega(q)} \}, \end{align} $$

and take $A_1 \subseteq A$ such that a shift of $A_1$ belongs to ${\mathbb {Z}}_{q/Q_1}$ and has density at least $\alpha $ . In particular, $|\pi _{Q_1} (A_1)|=1$ and of course such a shift exists by the Dirichlet principle. Similarly, we can do the same with the set B so as not to lose the density. Secondly, we apply Lemma 2 with $n=1$ , $A=A_1$ to regularize the set $A_1$ and find a set $A_* \subseteq A_1$ and a module $q_*$ that satisfies (2.1) and all other restrictions. Again, using the Dirichlet principle, we take $B_* \subseteq B$ such that the density of B does not decrease. Let $\lambda \in {\mathbb {Z}}_{q_*}$ be an arbitrary number and we first suppose that $\lambda \in {\mathbb {Z}}^*_{q_*}$ . To prove $\lambda \in (A-A)(B-B),$ it is enough to show that $\lambda \in (A_*-A_*)(B_*-B_*)$ or, equivalently, in terms of the Fourier transform, it suffices obtain the inequality

(2.7) $$ \begin{align} \frac{|A_*|^2 |B_*|^2}{q_*}> \frac{1}{q_*} \sum_{r\neq 0} |\widehat{B}_* (r)|^2 \cdot \sum_{a_1,a_2\in A_*} e_{q_*} \left(\frac{\lambda r}{a_1-a_2} \right) := \sigma . \end{align} $$

Now clearly,

(2.8) $$ \begin{align} \sigma \leqslant \frac{1}{q_*} \sum_{q_2|q_*,\, q_2>1}\, \sum_{z\in {\mathbb{Z}}^*_{q_2}} |\widehat{B}_* (zq_* q^{-1}_2)|^2 \left| \sum_{a_1,a_2\in A_*} e_{q_2} \left(\frac{\lambda z}{a_1-a_2} \right) \right| . \end{align} $$

In terms of the Kloosterman sums

$$\begin{align*}K_q (\lambda,r) := \sum_{x\in {\mathbb{Z}}^*_{q}} e_{q} \left( \frac{\lambda}{x} + rx\right) \end{align*}$$

and the density function

(2.9) $$ \begin{align} \eta_{q_2} (\xi) := |\{ a\in A_* ~:~ a \equiv \xi\quad \pmod {q_2} \}|, \end{align} $$

one has (recall that $\lambda \in {\mathbb {Z}}^*_{q_*}$ and $z \in {\mathbb {Z}}^*_{q_2}$ )

(2.10) $$ \begin{align} &\sum_{a_1,a_2\in A_*} e_{q_2} \left(\frac{\lambda z}{a_1-a_2} \right) =\\&\quad \sum_{\xi_1,\xi_2 \in {\mathbb{Z}}_{q_2}} \eta_{q_2}(\xi_1) \eta_{q_2} (\xi_2) e_{q_2} \left(\frac{\lambda z}{\xi_1-\xi_2} \right) = q^{-1}_2 \sum_{\xi \in {\mathbb{Z}}_{q_2}} |\widehat{\eta}_{q_2} (\xi)|^2 K_{q_2} (\lambda z, \xi) \nonumber\end{align} $$

$$\begin{align*}\leqslant 2 \sqrt{q_2} \tau(q_2) \| \eta_{q_2} \|_2^2 . \end{align*}$$

In the last line, we have applied the well-known bound for the Kloosterman sum and the Parseval identity. Now, to estimate $\| \eta _{q_2}\|_2^2$ , we use the regularity property of $A_*$ and derive

(2.11) $$ \begin{align} \| \eta_{q_2}\|_2^2 \leqslant \| \eta_{q_2}\|_\infty \| \eta_{q_2}\|_1 \leqslant \frac{|A_*|^2}{q^{1-\varepsilon}_2} . \end{align} $$

Further, let us obtain a lower bound for divisors $q_2$ . Since $|\pi _{Q_1} (A_1)|=1$ , it follows that for all $q_1|Q_1$ , we have

$$\begin{align*}\frac{1}{q_1} \sum_{\xi \in {\mathbb{Z}}_{q_1}} |\widehat{\eta}_{q_1} (\xi)|^2 K_{q_1} (\lambda z, \xi) = \frac{|A_*|^2}{q_1} \sum_{\xi \in {\mathbb{Z}}_{q_1}} K_{q_1} (\lambda z, \xi) = 0 . \end{align*}$$

Thus, one can see that summations in (2.8) is taken over $q_2 \geqslant M$ . Choosing $\varepsilon =1/4$ , say, and using the last fact, we get in view of the Parseval identity that

$$\begin{align*}\sigma \ll M^{-1/4} \frac{|A_*|^2}{q_*} \sum_{q_2|q_*,\, q_2>1}\, \sum_{z\in {\mathbb{Z}}^*_{q_2}} |\widehat{B}_* (zq_* q^{-1}_2)|^2 \leqslant M^{-1/4} |A_*|^2 |B_*| . \end{align*}$$

Returning to (2.7), we obtain a contradiction provided $|B_*| \gg q_* M^{-1/4}$ . In other words, we have for a certain $s\geqslant 0$ , $\alpha M^{s/4}> 1$ that

$$\begin{align*}|B| M^{s/4} \ll q M^{-1/4}, \end{align*}$$

and this implies $M \ll \beta ^{-4}$ . Thus, in view of our restriction to the divisors of $q_*$ , the condition $\alpha \geqslant \beta $ , the first bound for $Q_1$ from (2.6), and the bound for s, which follows from Lemma 2, we get

$$\begin{align*}d \ll M^{\pi (M)} \exp (O(\log^2 (1/\alpha) / \log (1/\beta)) \ll \exp(O(\beta^{-4})) \end{align*}$$

as required.

Now, let $\lambda \in {\mathbb {Z}}_{q_*}$ be an arbitrary element. Write $\lambda = q' \lambda '$ , where $q' |q$ and $\lambda '\in {\mathbb {Z}}^*_{q_*/q'}$ . Using the Dirichlet principle, choose a subset of $B' \subseteq B_*$ of density at least $\beta $ such that all elements of a shift of $B'$ are divisible by $q'$ . Then our inclusion can be rewritten as $\lambda ' \in (A_*-A_*)(B'-B')$ modulo $q_*/q'$ and we can apply the arguments above replacing module $q_*$ to $q_*/q'$ .

To obtain (2.5), we use the second bound for $Q_1$ from (2.6) and derive as above

$$\begin{align*}d \ll M^{\omega (q)} \exp (O(\log (1/\beta))) \ll \exp (O(\omega (q) \log (1/\beta))) . \end{align*}$$

This completes the proof.

As one can see from the proof of Theorem 2.3 that the constant four in (2.3) can be decreased to $2+o(1)$ but we leave such calculations to the interested reader.

3 On the general case

In [5, Problem 2], Fish considered a more general two-dimensional case (actually, in his paper, he had to deal with even more general dynamical setting) and formulated the following problem.

Problem 3.1 [Fish]. Let q be a positive number and $\mathcal {A}, \mathcal {B} \subseteq {\mathbb {Z}}_q^2$ be sets, $|\mathcal {A}| = \alpha q^2$ , ${|\mathcal {B}|=\beta q^2}$ , and suppose that $\alpha \geqslant \beta $ . Prove that in the case $\mathcal {A} = \mathcal {B}$ for a certain function F there is $d|q$ such that $d\leqslant F(\beta )$ and

(3.1) $$ \begin{align} d \cdot {\mathbb{Z}}_q \subseteq \{ (a_1-b_1) (a_2 - b_2) ~:~ (a_1,a_2) \in \mathcal{A},\, (b_1,b_2) \in \mathcal{B} \} , \end{align} $$

provided $\beta $ is sufficiently large.

In this section, we study the number $N_{\mathcal {A}, \mathcal {B}} (\lambda )$ of the solutions to the equation

(3.2) $$ \begin{align} (a_1-b_1) (a_2 - b_2) \equiv \lambda \pmod q \,, \quad \quad (a_1,a_2) \in \mathcal{A},\, (b_1,b_2) \in \mathcal{B} , \end{align} $$

and give a partial answer to the problem above. We consider the squarefree case for simplicity and emphasis one more time that our sets $\mathcal {A}$ , $\mathcal {B}$ are arbitrary (in the case of Cartesian products and squarefree $q,$ one can apply other methods, see [10]). Also, in the case of prime $q,$ we obtain a result of Vinh-type [22], see asymptotic formula (3.5).

Theorem 3.2 Let q be a squarefree number, let $\mathcal {A}, \mathcal {B} \subseteq {\mathbb {Z}}_q^2$ be sets, $|\mathcal {A}| = \alpha q^2$ , $|\mathcal {B}|=\beta q^2$ , and suppose that $\alpha \geqslant \beta $ . Then

(3.3) $$ \begin{align} d \cdot {\mathbb{Z}}^*_q \subseteq \{ (a_1-b_1) (a_2 - b_2) ~:~ (a_1,a_2) \in \mathcal{A},\, (b_1,b_2) \in \mathcal{B} \} \end{align} $$

with

$$\begin{align*}d \ll \exp (O(\omega(q) \log \omega(q) - \log \beta)) . \end{align*}$$

In particular, for $\mathcal {A} = \mathcal {B},$ one has with the same d that

(3.4) $$ \begin{align} d \cdot {\mathbb{Z}}_q \subseteq \{ (a_1-b_1) (a_2 - b_2) ~:~ (a_1,a_2) \in \mathcal{A},\, (b_1,b_2) \in \mathcal{B} \} . \end{align} $$

In the case when q is a prime number, we have

(3.5) $$ \begin{align} \left| N_{\mathcal{A}, \mathcal{B}} (\lambda) - \frac{|\mathcal{A}| |\mathcal{B}|}{q} \right| < 4 q^{7/8} \sqrt{|\mathcal{A}||\mathcal{B}|} . \end{align} $$

In particular, equality (3.1) holds for $|\mathcal {A}| |\mathcal {B}| \geqslant 16 q^{15/4}$ and $d=1$ .

Proof We start with (3.3). The proof follows the arguments of the proof of Theorem 2.3, and thus, we use the notation from this result. In particular, writing $q=p_1^{\rho _1} \dots p_t^{\rho _t}$ , $t=\omega (q)$ with $\rho _j=1$ , $j\in [t]$ we define $Q_1 = \prod _{j=1}^s p_j$ such that (2.6) holds and further we take $\lambda \in {\mathbb {Z}}^*_q$ . The only difference is that one should use Lemma 2 with $n=2$ to regularize the two-dimensional set $\mathcal {A}$ and let $\varepsilon =1/4$ . For a moment, we assume that $M \geqslant 100 t^2$ , say, and we will choose the parameter M later. Finally, with some abuse of the notation, we do not use new letters $\mathcal {A}_*, \mathcal {B}_*$ , $q_*$ below but the old ones $\mathcal {A}, \mathcal {B},$ and q (in other words, one can think that $\mathcal {A}$ is a regularized set already). Also, we utilize the fact that ${\mathbb {Z}}_q = {\mathbb {Z}}_{p^{\rho _1}_1} \times \dots \times {\mathbb {Z}}_{p^{\rho _t}_t} = {\mathbb {Z}}_{p^{}_1} \times \dots \times {\mathbb {Z}}_{p^{}_t}$ thanks the Chinese remainder theorem.

Now, for $a = (a_1,a_2)$ and $b=(b_1,b_2),$ let us write $I(a,b) = 1$ if the pair $a,b$ satisfies (3.2) and $I(a,b) = 0$ , otherwise. Then clearly,

(3.6) $$ \begin{align} N_{\mathcal{A}, \mathcal{B}} (\lambda) = \sum_{a\in \mathcal{A}, b\in \mathcal{B}} I(a,b) . \end{align} $$

Without loosing of the generality, we assume that $\lambda =1$ . Obviously, $I(a,b) = I(b,a)$ and we can rewrite the matrix $I(a,b)$ as $I(a,b) = \sum _{j=1}^{q^2} \mu _j u_j (a) \overline {u}_j (b)$ , where $\mu _j$ are eigenvalues and $u_j (x)$ are correspondent normalized eigenfunctions of I. One can easily check that $u_1 (x) = q^{-1} (1,\dots , 1)$ , $\|u_1\|_2 = 1$ and $\mu _1 = |{\mathbb {Z}}^*_q| = \varphi (q)$ . Writing $I'(a,b) = I(a,b) - \mu _1 u_1 (a) \overline {u}_1 (b)$ , we obtain

(3.7) $$ \begin{align} N_{\mathcal{A}, \mathcal{B}} (\lambda) - \frac{|\mathcal{A}| |\mathcal{B}| \varphi (q)}{q^2} = \sum_{a\in \mathcal{A}, b\in \mathcal{B}} I'(a,b) := N^{\prime}_{\mathcal{A}, \mathcal{B}} (\lambda) . \end{align} $$

By the Cauchy–Schwarz inequality, we get the following.

Here, $(I')^2$ is the second power of the matrix $I'$ . Similarly, $I^2 (a,a') = \sum _{b} I(a,b) I(a',b)$ and the last quantity coincides with the number of the solutions to the equation

(3.8) $$ \begin{align} a_2 - a^{\prime}_2 = \frac{a^{\prime}_1-a_1}{(a_1+x)(a^{\prime}_1+x)} , \end{align} $$

where $b=(x,y)$ , $a=(a_1,a_2)$ and $a'=(a^{\prime }_1,a^{\prime }_2)$ . Assume that $a\neq a'$ and rewrite our equation (3.8) as

(3.9) $$ \begin{align} x^2 + (a_1+a^{\prime}_1)x + a_1 a^{\prime}_1 + \frac{a_1-a^{\prime}_1}{a_2-a^{\prime}_2} = 0 , \end{align} $$

and its discriminant is $D'(a,a') := (a_1-a^{\prime }_1) (a_2-a^{\prime }_2)^{-1} [(a_1-a^{\prime }_1) (a_2-a^{\prime }_2) - 4]$ . Notice that if $a=a'$ , then we have $\varphi (q)$ solutions to equation (3.8). By $\chi _p$ denote the Legendre symbol modulo a prime p and let $\chi _0$ be the main character (modulo p). We have the identity $\chi _p (x^{-1}) = \chi _p (x)$ , $x\in {\mathbb {Z}}_p^*$ and hence $\chi _p (D'(a,a')) = \chi _p ( (a_1-a^{\prime }_1) (a_2-a^{\prime }_2)^{} [(a_1-a^{\prime }_1) (a_2-a^{\prime }_2) - 4] := \chi _p (D(a,a'))$ . In view of the Chinese remainder theorem, and our choice of the regularized set $\mathcal {A},$ one has

(3.10) $$ \begin{align} I^2 (a,a') = \prod_{j=s+1}^t \left( \chi_{p_j} (D(a,a')) + \chi_0 (D(a,a')) + (p_j-1) \delta_{p_j} (a_1-a^{\prime}_1, a_2-a^{\prime}_2) \right) \end{align} $$

(3.11) $$ \begin{align} = \mathcal{E} (a,a') + \prod_{j=s+1}^t (\chi_0 (D(a,a'))+ (p_j-1) \delta_{p_j} (a_1-a^{\prime}_1, a_2-a^{\prime}_2)) = \mathcal{E} (a,a') + \mathcal{E}' (a,a') , \end{align} $$

where for a positive integer $m,$ we have put $\delta _m (z,w) = 1$ if $z \equiv w \equiv 0 \pmod m$ , and 0 otherwise. Equivalently, writing T for the segment $[s+1,t]$ , one has

$$\begin{align*}\mathcal{E} (a,a') = \sum_{\emptyset \neq S \subseteq T}\, \prod_{j\notin S} (\chi_0 (D(a,a')) + (p_j-1) \delta_{p_j} (a_1-a^{\prime}_1, a_2-a^{\prime}_2)) \cdot \prod_{j\in S} \chi_{p_j} ( D(a,a')) \end{align*}$$

$$\begin{align*}= \sum_{\emptyset \neq S \subseteq T}\, \prod_{j\notin S} w_{p_j} (a,a') \cdot \prod_{j\in S} \chi_{p_j} ( D(a,a')) . \end{align*}$$

Notice that $\mathcal {E} (a,a) = 0$ . From (3.10) and (3.11), it follows that $\mathcal {E} u_1 = 0$ . Indeed, we know that $I^2 u_1 = \mu _1^2 u_1 = \varphi ^2 (q) u_1$ and

(3.12) $$ \begin{align} \sum_a \prod_{j=s+1}^t (\chi_0 (D(a,a'))+ (p_j-1) \delta_{p_j} (a_1-a^{\prime}_1, a_2-a^{\prime}_2)) \end{align} $$

(3.13) $$ \begin{align} = \prod_{j=s+1}^t \left( \sum_{z,w\in {\mathbb{Z}}_{p_j}} \chi_0((zw)^2 - 4zw) + p_j-1 \right) \end{align} $$

(3.14) $$ \begin{align} \qquad= \prod_{j=s+1}^t \left( (p_j-1) \sum_{z\in {\mathbb{Z}}_{p_j}} \chi_0(z^2 - 4z) + p_j-1 \right) = \prod_{j=s+1}^t (p_j-1)^2 = \varphi^2 (q) . \end{align} $$

Hence, in very deed $\mathcal {E} u_1 = 0,$ and thus

(3.15) $$ \begin{align} \sigma = \langle (I')^2 \mathcal{A}, \mathcal{A} \rangle = \langle (I')^2 f_{\mathcal{A}}, f_{\mathcal{A}} \rangle = \langle I^2 f_{\mathcal{A}}, f_{\mathcal{A}} \rangle = \langle \mathcal{E} \mathcal{A}, \mathcal{A} \rangle + \langle \mathcal{E}' f_{\mathcal{A}}, f_{\mathcal{A}} \rangle, \end{align} $$

where $f_{\mathcal {A}} (a) = \mathcal {A} (a) - \langle \mathcal {A}, u_1 \rangle u_1 (a)$ , $\sum _a f_{\mathcal {A}} (a) = 0$ . Let us estimate the term ${r:=\langle \mathcal {E}' f_{\mathcal {A}}, f_{\mathcal {A}} \rangle }$ rather roughly. Since the function $f_{\mathcal {A}}$ is orthogonal to $u_1$ and $\| f_{\mathcal {A}}\|_\infty \leqslant 1$ , it follows that:

$$\begin{align*}|r|= \left| \sum_{a,a'} f_{\mathcal{A}} (a) f_{\mathcal{A}} (a') \prod_{j=s+1}^t \left(1- \delta_{p_j} (D(a,a')) +(p_j-1) \delta_{p_j} (a_1-a^{\prime}_1, a_2-a^{\prime}_2) \right) \right| \end{align*}$$

$$\begin{align*}\leqslant \sum_{\emptyset \neq S\subseteq T} \left| \sum_{a,a'} f_{\mathcal{A}} (a) f_{\mathcal{A}} (a') \prod_{j\in S} (- \delta_{p_j} (D(a,a')) +(p_j-1) \delta_{p_j} (a_1-a^{\prime}_1, a_2-a^{\prime}_2) ) \right| \end{align*}$$

$$\begin{align*}\leqslant 2|\mathcal{A}| q^2 \sum_{n=1}^{t-s}\, \sum_{S\subseteq T,\, |S|=n}\, \prod_{j\in S} \left( \frac{3}{p_j} + \frac{p_j-1}{p^2_j} \right) \leqslant 2|\mathcal{A}| q^2 \sum_{n=1}^{t-s}\, \binom{t-s}{n} \left(\frac{4}{M} \right)^n \end{align*}$$

(3.16) $$ \begin{align} \leqslant 10 |\mathcal{A}| q^2 t M^{-1} . \end{align} $$

Now, returning to the definition of the operator $\mathcal {E} (a,a')$ , recalling estimate (3.8) and using the Cauchy–Schwarz inequality, we obtain

$$\begin{align*}\sigma^2 \leqslant |\mathcal{A}| \sum_{a,a' \in \mathcal{A}} \sum_{x,y} \sum_{\emptyset \neq S_1,S_2 \subseteq T}\, \prod_{i\in S_1,\, j\in S_2} \chi_{p_i} (D((x,y),(a_1,a_2)) \chi_{p_j} (D((x,y),(a^{\prime}_1,a^{\prime}_2)) \end{align*}$$

(3.17) $$ \begin{align} \prod_{i\notin S_1,\, j\notin S_2} w_{p_i} ((x,y),(a_1,a_2)) w_{p_j} ((x,y),(a^{\prime}_1,a^{\prime}_2)) . \end{align} $$

The term with $a \equiv a' \pmod q$ gives us a contribution at most $4^{t} |\mathcal {A}| q^2$ into the last sum (see (3.12)—(3.14) to estimate $\| w_{p_j}\|_1$ for $j\notin S$ and use the trivial fact that $\|\chi _p \|_{\infty } \leqslant 1$ to bound the rest). Now, let $a \neq a' \pmod q$ but $a \equiv a' \pmod {q_*}$ with maximal $q_*|q$ . Thus $q_* \neq q$ and $Q_1|q_*$ . We can write $q_* = q_* (W) = Q_1 \prod _{j\in W} p_j$ for a certain (possibly empty) set $W \subseteq T$ . Let us say that all primes p such that $p|(q/q_*)$ (that is, $p|q$ and $p\notin W$ ) are good. In particular, for all good primes $p,$ one has $p>M$ . Now for a good prime $p,$ the sum above $\sum _{x,y \mod {\mathbb {Z}}_p}\chi _p (D(x,y), (a_1,a_2))$ (or, analogously, the sum $\sum _{x,y \mod {\mathbb {Z}}_p}\chi _p (D(x,y), (a^{\prime }_1,a^{\prime }_2))$ ) is either at most $3p^{3/2}$ by Weil, or the sum over y is p if $\frac {2}{x-a_1} + a_2 = \frac {2}{x-a^{\prime }_1} + a^{\prime }_2$ modulo p. The last equation is nontrivial one by our choice of $p,$ hence it has at most two solutions, and thus, in any case, the sum over $x,y \mod {\mathbb {Z}}_p$ is at most $3p^{3/2} < 3p^2/\sqrt {M}$ . Further, we split the sets $S_1,S_2$ as $S_1 = S^*_1 \bigsqcup G_1$ , $S_2 = S^*_2 \bigsqcup G_2$ , where (possibly empty) sets $G_1, G_2$ correspond to good primes and the sets $S^*_1 \subseteq W$ , $S^*_2 \subseteq W$ correspond to the divisors of $q_* (W)$ . Since $S_1, S_2 \neq \emptyset $ , it follows that either $G_1 \bigcup G_2 \neq \emptyset $ or $S^*_1,S^*_2 \neq \emptyset $ . Using the notation as in (2.9), namely,

(3.18) $$ \begin{align} \eta_{\tilde{q}} (\xi) := |\{ a\in \mathcal{A} ~:~ a \equiv \xi\quad \pmod {\tilde{q}} \}| \,, \quad \quad \tilde{q}|q,\, \xi \in {\mathbb{Z}}^2_{\tilde{q}} , \end{align} $$

we see that the number of pairs $a\equiv a' \pmod {\tilde {q}}$ is exactly $\| \eta _{\tilde {q}} \|_2^2$ for any $\tilde {q} |q$ and one can use bound (2.11) to estimate the last quantity. Now, recalling inequality (2.1) and splitting sum (3.17) according the case $W \neq \emptyset $ or not, we get

$$\begin{align*}\sigma^2 |\mathcal{A}|^{-1} \leqslant \end{align*}$$

(3.19) $$ \begin{align} 4^{t} |\mathcal{A}| q^2 + q^2 \sum_{\emptyset \neq W \subseteq T}\, \sum_{a,a' \in \mathcal{A},\, a \equiv a' \pmod {q(W)}} 4^{|W|} + q^2 \sum_{a,a' \in \mathcal{A}} \sum_{n+m\geqslant 1} \binom{t-s}{n} \binom{t-s}{m} \left(\frac{3}{\sqrt{M}} \right)^{n+m} \end{align} $$

$$\begin{align*}\leqslant 4^{t} |\mathcal{A}|^{} q^2 + q^2 |\mathcal{A}|^{2} \sum_{\emptyset \neq W \subseteq T} 4^{|W|} M^{-3|W|/4} + 4 q^2 |\mathcal{A}|^{2} t^{} M^{-1/2} \ll q^2 |\mathcal{A}|^{2} t^{} M^{-1/2} . \end{align*}$$

Using (3.6), (3.7), (3.8), (3.16), and the Cauchy–Schwarz inequality, we get

(3.20) $$ \begin{align} N_{\mathcal{A}, \mathcal{B}} (\lambda) - \frac{|\mathcal{A}| |\mathcal{B}| \varphi (q)}{q^2} \ll (t^{} M^{-1/2})^{1/4} \cdot |\mathcal{A}|^{3/4} \sqrt{|\mathcal{B}| q} + (t M^{-1})^{1/2} \cdot \sqrt{|\mathcal{A}| |\mathcal{B}|} q . \end{align} $$

We have $\varphi (q) \gg q/\log t,$ and hence after some calculations, we see that $N_{\mathcal {A}, \mathcal {B}} (\lambda )> 0$ provided $M\gg t^{2} \beta ^{-6} \log ^8 t$ . As in Theorem 2.3, one has $Q_1 \leqslant M^t$ , and thus

$$\begin{align*}d \ll \exp ( t \log M ) = \exp (O(t \log t - \log \beta) ) . \end{align*}$$

In the case of prime $q,$ the argument is even simpler because one do not need the regularization, the second term in (3.19) plus the quantity r is negligible, see estimate (3.16). Finally, let $\mathcal {A} = \mathcal {B}$ and if $\lambda \notin {\mathbb {Z}}^*_q$ , then write $\lambda = q' \lambda '$ , where $q' |q$ and $\lambda '\in {\mathbb {Z}}^*_{q_*/q'}$ . Using the Dirichlet principle, choose a subset of $\mathcal {A}' \subseteq \mathcal {A}$ of density at least $\alpha $ such that $|\pi _{q'} (\mathcal {A}')|=1$ . Then the required inclusion (3.4) can be rewritten as

$$\begin{align*}\lambda' \in \{ (a_1-b_1) (a_2 - b_2) ~:~ (a_1,a_2), (b_1,b_2) \in \mathcal{A} \}, \end{align*}$$

and we can apply the arguments above replacing $q_*$ to $q_*/q'$ . This completes the proof.

Remark 3.3 Of course, inclusion (3.4) does not hold for $\mathcal {A} \neq \mathcal {B}$ , just take ${\mathcal {A} = (d \cdot {\mathbb {Z}}_q) \times (d \cdot {\mathbb {Z}}_q)}$ and $\mathcal {B} = (d \cdot {\mathbb {Z}}_q + 1) \times (d \cdot {\mathbb {Z}}_q + 1)$ for an arbitrary $d|q$ , $1< d \ll 1$ . Also, the author thinks that the error term in (3.5) can be improved but this weaker bound is enough for us to resolve our equation for sets of positive densities.

Remark 3.4 The attentive reader may be alerted that we have two different main terms in (2.7) and in (3.20). Nevertheless, they are asymptotically the same due to the fact that in (3.20), our parameter M depends on growing quantity $\omega (q)$ .

Similarly, we obtain an affirmative answer to [5, Problem 1] in the case of squarefree q. By $M_{\mathcal {A}, \mathcal {B}} (\lambda ),$ denote the number of the solutions to the equation

(3.21) $$ \begin{align} (a_1-b_1)^2 - (a_2 - b_2)^2 \equiv \lambda\quad \pmod q \,, \quad \quad (a_1,a_2) \in \mathcal{A},\, (b_1,b_2) \in \mathcal{B} . \end{align} $$

Theorem 3.5 Let q be a squarefree number, let $\mathcal {A}, \mathcal {B} \subseteq \mathbb {F}_q^2$ be sets, $|\mathcal {A}| = \alpha q^2$ , $|\mathcal {B}|=\beta q^2$ , and suppose that $\alpha \geqslant \beta $ . Then

(3.22) $$ \begin{align} d {\mathbb{Z}}^*_q \subseteq \{ (a_1-b_1)^2 - (a_2 - b_2)^2 ~:~ (a_1,a_2) \in \mathcal{A},\, (b_1,b_2) \in \mathcal{B} \} \end{align} $$

with

$$\begin{align*}d \ll \exp (O(\omega(q) \log \omega(q) - \log \beta)) . \end{align*}$$

In particular, for $\mathcal {A} = \mathcal {B},$ one has with the same d that

(3.23) $$ \begin{align} d {\mathbb{Z}}_q \subseteq \{ (a_1-b_1)^2 - (a_2 - b_2)^2 ~:~ (a_1,a_2) \in \mathcal{A},\, (b_1,b_2) \in \mathcal{B} \} . \end{align} $$

In the case when q is a prime number, one has

(3.24) $$ \begin{align} M_{\mathcal{A}, \mathcal{B}} (\lambda) - \frac{|\mathcal{A}| |\mathcal{B}|}{q} < 4 q^{7/8} \sqrt{|\mathcal{A}||\mathcal{B}|} . \end{align} $$

Proof The argument differs from the proof of Theorem 3.2 in some unimportant details only, so we use the notation from the former result. Indeed, for $a = (a_1,a_2)$ and $b=(b_1,b_2),$ we write $\tilde {I}(a,b) = 1$ if the pair $a,b$ satisfies (3.21) and $\tilde {I}(a,b) = 0,$ otherwise. Calculating $\tilde {I}^2 (a,a')$ , we arrive to the equation

(3.25) $$ \begin{align} a_1^2 - (a^{\prime}_1)^2 + 2(a^{\prime}_1 - a_1) x - a_2^2 + (a^{\prime}_2)^2 + 2(a_2 - a^{\prime}_2) y = 0, \end{align} $$

and hence, we can find x via y or y via x, provided $a\neq a' \pmod q$ . Assuming that $a^{\prime }_2 \neq a_2$ , say, we derive

$$\begin{align*}y= \frac{(a^{\prime}_1)^2-a_1^2 +a_2^2 - (a^{\prime}_2)^2}{2(a_2 - a^{\prime}_2)} + \frac{a_1-a^{\prime}_1}{a_2 - a^{\prime}_2} \cdot x = s + t x , \end{align*}$$

and hence substituting the last expression into (3.21) and computing the discriminant $\tilde {D} (a,a')$ (without loss of the generality, we put $\lambda =1$ ), one obtains

$$\begin{align*}\tilde{D}(a,a') = (t (a_2-s)-a_1)^2 + (1-t)^2 (1+(a_2-s)^2 - a_1^2) \end{align*}$$

(3.26) $$ \begin{align} \quad\qquad= 2t (t-1) (a_2-s)^2 - 2a_1 t(a_2-s) + (1-t)^2 (1-a_1^2) + (a_2-s)^2 + a_1^2 .\!\!\!\!\! \end{align} $$

As in the proof of Theorem 3.2, we consider $\mathcal {E} (a,a')$ , take good primes and so on. The first eigenvalue $\mu _1$ equals the number of the solutions to the equation $x^2-y^2 \equiv 1 \pmod q$ , that is, $\varphi (q)$ again. Also, $\tilde {I}^{2} (a,a) = \mu _1$ and for $a\neq a'$ the quantity $\tilde {I}^{2} (a,a')$ expressed exactly as in (3.10) (with another discriminant $\tilde {D}$ , of course), and thus, one can check that $\mathcal {E} u_1$ vanishes making calculations as in (3.12)—(3.14). Further, as in Theorem 3.2, we apply the standard Weil bound to estimate the sum of characters. For any good prime $p,$ it gives us a nontrivial bound of the form $O(p^{3/2}) = O(p^2/\sqrt {M}),$ and hence, we obtain (3.22) and thus (3.23) by the same argument as at the end of Theorem 3.2 (one can check or see below that all obtained varieties are non–degenerated). Finally, to get (3.24), we need to estimate

$$\begin{align*}\sum_{a,a' \in \mathcal{A}} \sum_{x,y} \chi_{q} (\tilde{D}((x,y),(a_1,a_2))) \chi_{q} (\tilde{D}((x,y),(a^{\prime}_1,a^{\prime}_2))), \end{align*}$$

and by the Weil estimate, it is at most $20 q^{3/2}$ , say, excluding the case $\tilde {D}((x,y),(a_1,a_2))$ is proportional to $\tilde {D}((x,y),(a^{\prime }_1,a^{\prime }_2))$ . In particular, it means that the coefficients of these polynomials are proportional ones and using (3.26) and comparing the coefficients before the highest degrees in x, say, we get $\frac {a_2-2a_1-y}{(y-a_2)^4} = \frac {a^{\prime }_2-2a^{\prime }_1-y}{(y-a^{\prime }_2)^4}$ . Again, thanks to $a \neq a',$ we see that this equation is nontrivial one, and hence, it has at most four solutions. It follows that our sum is at most $4q$ in this case. Thus, as in (3.19) and (3.20), we have

$$\begin{align*}M_{\mathcal{A}, \mathcal{B}} (\lambda) - \frac{|\mathcal{A}| |\mathcal{B}| \varphi (q)}{q^2} \leqslant 3 (q^{3/2} |\mathcal{A}| )^ {1/4} \sqrt{|\mathcal{A}| |\mathcal{B}|} \leqslant 3 q^{7/8} \sqrt{|\mathcal{A}| |\mathcal{B}|} . \end{align*}$$

This completes the proof.

Remark 3.6 We have used a direct way of the proof of Theorem 3.5, another approach is to notice that $\tilde {I}(a,b) = I(ga,gb)$ , where the linear transformation g is given by the formula $g(x,y) = (x+y,x-y)$ . After that one can apply Theorem 3.2 with the sets $g^{-1}(\mathcal {A})$ , $g^{-1}(\mathcal {B})$ .

Also, let us remark that one can consider the equation $(a_1-b_1)^2 + (a_2 - b_2)^2 = \lambda \,{\neq}\, 0,$ instead of (3.21), that is the question about the distance between points $(a_1,a_2) \in \mathcal {A}$ and $ (b_1,b_2) \in \mathcal {B}$ . We leave it to the interested reader to check that all parts of the proof have remained almost the same (formula (3.25), the identity $\mu _1 = \varphi (q)$ are exactly the same).

4 On an application of group actions

In this section, we discuss another approach to results of Fish-type, namely, we consider an intermediate situation between Theorems 2.3 and 3.2, our set $\mathcal {A} \subseteq {\mathbb {Z}}^2_q$ is an arbitrary but the set $\mathcal {B} \subseteq {\mathbb {Z}}^2_q$ is a Cartesian product. In this case, one can deal with rather general q (and not just squarefree). For simplicity, we do not do any regularization as in the previous section immediately assuming that all prime factors of q are large.

In the proof, we follow the methods from [3] and [17].

Theorem 4.1 Let q be a positive odd integer, and let $\mathcal {A}, \mathcal {B} \subseteq {\mathbb {Z}}_q^2$ be sets, $|\mathcal {A}| = \delta q^2$ , $\mathcal {B} = A\times B$ , $|A| = \alpha q$ , $|B| = \beta q$ . Suppose that all prime divisors of q are at least M, where

$$\begin{align*}M \geqslant C_1 \tau (q) \delta^{-2} (\alpha \beta)^{-C_2} , \end{align*}$$

and $C_1, C_2>0$ are absolute constants. Then

(4.1) $$ \begin{align} {\mathbb{Z}}^*_q \subseteq \{ (a_1-b_1) (a_2 - b_2) ~:~ (a_1,a_2) \in \mathcal{A},\, (b_1,b_2) \in \mathcal{B} \} . \end{align} $$

Proof Let $q=p^{\rho _1}_1 \dots p^{\rho _t}_t$ , where $p_j$ are different odd primes and $\rho _j$ are positive integers. By our assumption $p_j \geqslant M$ for all $j\in [t]$ . Without loosing of the generality, one can take $\lambda = -1$ in formula (3.2). Recall that $\mathrm {SL}_2({\mathbb {Z}}_q)$ acts on ${\mathbb {Z}}_q$ via Möbius transformations: $x\to gx = \frac {ax+b}{cx+d}$ , where $g=\left (\begin {array}{cc} a & b \\ c & d \end {array}\right )$ (for composite $q,$ the equivalence is taken over ${\mathbb {Z}}^*_q$ , of course). Since $\mathcal {B} = A\times B,$ we can rewrite our equation (3.2) as

(4.2) $$ \begin{align} a=gb \,, \quad \quad a\in A\,, b\in B\,, g\in G , \end{align} $$

where $G \subset \mathrm {SL}_2 ({\mathbb {Z}}_q)$ is the set of matrices of the form

$$\begin{align*}g= \left( {\begin{array}{cc} -\alpha & \alpha \beta+1 \\ -1 & \beta \\ \end{array} } \right) \,, \quad \quad (\alpha,\beta) \in \mathcal{A} , \end{align*}$$

see [17, Section 5] or just make a direct calculation. Clearly, $|G| = |\mathcal {A}|$ . Further by [17, Lemma 15], the multiplicative energy $\mathsf {E}(G)$ of the set G, that is,

$$\begin{align*}\mathsf{E}(G) = |\{ (g_1,g_2,g_3,g_4) \in G\times G \times G \times G ~:~ g_1 g_2^{-1} = g_3 g_4^{-1} \}| \end{align*}$$

coincides with the number of the solutions to the system

$$\begin{align*}&\beta_1 - \beta_2 = \beta_3 - \beta_4 := s \,, \quad \quad s(\alpha_1 - \alpha_3) = s(\alpha_2 - \alpha_4) = 0 \,, \\& \alpha_1 - \alpha_2 - \alpha_1 \alpha_2 s = \alpha_3 - \alpha_4 - \alpha_3 \alpha_4 s , \end{align*}$$

where $(\alpha _i,\beta _i) \in \mathcal {A}$ , $i\in [4]$ . Let $s = d s'$ , where d is a divisor of q and $s'$ is coprime to q. Taking $(\alpha _1,\beta _1), (\alpha _4,\beta _4) \in \mathcal {A}$ , we find $\beta _2$ , $\beta _3$ from the first equation and $\alpha _2,\alpha _3$ modulo $q/d$ from the second one. Also, using $\alpha _3$ we can reconstruct $\alpha _2$ from the third equation, provided $d>1$ . In other words, for fixed $d,$ there are $q/d$ possibilities for $s'$ and d possibilities for $\alpha _3$ . Finally, if $d=1$ , then we have at most $q|G|^2$ solutions. Thus, we obtain the bound

(4.3) $$ \begin{align} \mathsf{E}(G) \leqslant |G|^2 \sum_{d|q} \frac{q}{d} \cdot d \leqslant \tau(q) q |G|^2 . \end{align} $$

Now, let us say a few words about representations of the group $\mathrm {SL}_2 ({\mathbb {Z}}_q)$ (see [3, Sections 7 and 8]). First of all, for any irreducible representation $\rho _q$ of $\mathrm {SL}_2 ({\mathbb {Z}}_q),$ we have $\rho = \rho _q = \rho _{p^{\rho _1}_1} \otimes \dots \otimes \rho _{p^{\rho _t}_t}$ , and hence, it is sufficient to understand the representation theory for $\mathrm {SL}_2 ({\mathbb {Z}}_{p^n})$ , where p is a prime number and n is a positive integer. Now, by [3, Lemma 7.1], we know that for any odd prime, the dimension of any faithful irreducible representation of $\mathrm {SL}_2 ({\mathbb {Z}}_{p^n})$ is at least $2^{-1} p^{n-2} (p-1)(p+1)$ . For an arbitrary $r\leqslant n,$ we can consider the natural projection $\pi _r : \mathrm {SL}_2 ({\mathbb {Z}}_{p^n}) \to \mathrm {SL}_2 ({\mathbb {Z}}_{p^r}),$ and let $H_r = \mathrm {Ker\,} \pi _r$ . One can show that the set $\{ H_r \}_{r\leqslant n}$ gives all normal subgroups of $\mathrm {SL}_2 ({\mathbb {Z}}_{p^n}),$ and hence, any nonfaithful irreducible representation arises as a faithful irreducible representation of $\mathrm {SL}_2 ({\mathbb {Z}}_{p^r})$ for a certain $r<n$ . Anyway, we see that the multiplicity (dimension) $d_\rho $ of any nontrivial irreducible representation $\rho $ of $\mathrm {SL}_2 ({\mathbb {Z}}_{p^n})$ is at least $p/3 \geqslant M/3$ .

Applying estimate (4.3), using the formula for $\mathsf {E}(G)$ via the representations and taking into account, the obtained lower bound for the multiplicities of the representations, we get

$$\begin{align*}\frac{M\| \widehat{G}\|^4_{op}}{3|\mathrm{SL}_2 ({\mathbb{Z}}_q)|} \leqslant \frac{1}{|\mathrm{SL}_2 ({\mathbb{Z}}_q)|} \sum_{\rho} d_\rho \| \widehat{G} (\rho) \widehat{G}^* (\rho) \|_{}^{2} = \mathsf{E}(G) \leqslant \tau(q) q |G|^2 , \end{align*}$$

and hence

(4.4) $$ \begin{align} \| \widehat{G}\|_{op} \leqslant |G| \cdot \left( \frac{3\tau(q)}{M\delta^2} \right)^{1/4} := \frac{|G|}{K} , \end{align} $$

where by $\| \widehat {G}\|_{op}$ , we have denoted the maximum of the operator norm of matrices $\widehat {G} (\rho )$ for all nontrivial representations $\rho $ and $\| \cdot \|$ is the usual Hilbert–Schmidt norm. Thanks to our choice of $M,$ one can see that bound (4.4) is nontrivial, that is, $K>1$ . Returning to (4.2) and using the standard scheme (see, e.g., [17, Lemma 13 and Sections 5 and 6]), we obtain

$$\begin{align*}N_{\mathcal{A}, \mathcal{B}} (\lambda) - \frac{|A||B||G| q}{J_2(q)} \leqslant \sqrt{|A||B|} |G| q^{-1/k} , \end{align*}$$

where $k \sim \log q/\log K$ and $|\mathrm {SL}_2 ({\mathbb {Z}}_q)| = q J_2 (q) = q^3 \prod _{p|q} (1-p^{-2})$ . Hence $N_{\mathcal {A}, \mathcal {B}} (\lambda )> 0$ , provided $K \gg (\sqrt {\alpha \beta })^{-O(1)}$ . The last condition is equivalent to $M\gg \tau (q) \delta ^{-2} (\sqrt {\alpha \beta })^{-O(1)}$ . This completes the proof.

5 On the covering numbers of difference sets

Let us recall the definition of the covering number of a set (see, e.g., [1] or [11]).

Definition 5.1 Let ${\mathbf G}$ be a finite abelian group with the group operation $+$ , and let $A\subseteq {\mathbf G}$ be a set. We write

$$\begin{align*}\mathrm{cov}^{+}(A) = \mathrm{cov} (A) = \min \{ |X| ~:~ X\subseteq {\mathbf G},\, A+X = {\mathbf G} \} \end{align*}$$

and the quantity $\mathrm {cov}^{+} (A)$ is called the (additive) covering number of A.

Having a finite ring $\mathcal {R}$ with two operations $+, \times $ , we underline which covering number we use, writing $\mathrm {cov}^{+}$ or $\mathrm {cov}^\times $ . It is known [1, Corollary 3.2] that for any set $A \subseteq {\mathbf G}$ , one has $\mathrm {cov}^{+} (A) = O\left (\frac {|{\mathbf G}|}{|A|} \log |A| \right )$ and the last bound is tight. In this section, we study difference sets $A-A$ , $A \subseteq {\mathbb {Z}}_q$ and show that $\mathrm {cov}^{\times } (A-A)$ is always small. First of all, let us make a remark about a connection between $\mathrm {cov}^{+}$ and $\mathrm {cov}^{\times }$ in a ring  $\mathcal {R}$ .

Proposition 5.2 Let $\mathcal {R}$ be a finite ring, and let $S \subseteq \mathcal {R}$ be a set. Then

(5.1) $$ \begin{align} \mathrm{cov}^\times (S-S) \leqslant \mathrm{cov}^{+} (S) , \end{align} $$

provided all numbers $1,\dots , \mathrm {cov}^{+} (S)$ belong to $\mathcal {R}^*$ .

Proof Let $S+X = {\mathbb {Z}}_q$ and $|X| = \mathrm {cov}^{+} (S) := k$ . For any $g\in {\mathbb {Z}}_q$ , consider $jg$ , where $j=0,1,\dots , k$ . By the pigeonhole principle, there are different $j_1 \neq j_2$ such that ${j_1 g \in S+x}$ and $j_2 g \in S+x$ with the same $x\in X$ . It implies that $(j_1-j_2)g \in S-S,$ and hence $g\in (j_1-j_2)^{-1} (S-S)$ , provided $(j_1-j_2)^{-1} \in \mathcal {R}^*$ . It remains to notice that $[-k,k]^{-1} \cdot (S-S) = [k]^{-1} \cdot (S-S)$ . This completes the proof.

By the well-known consequence of the Ruzsa covering lemma [21, Section 2.4], we have for any finite group ${\mathbf G}$ and a set $A\subseteq {\mathbf G}$ that for a certain set $Z\subseteq {\mathbf G}$ , one has

(5.2) $$ \begin{align} {\mathbf G} \subseteq A-A + Z , \quad \quad |Z| \leqslant |{\mathbf G}|/|A| . \end{align} $$

In particular, it means that $\mathrm {cov}^{+} (A-A) \leqslant |{\mathbf G}|/|A|$ . Thus, Proposition 5.2 gives us the following result.

Corollary 5.3 Let $\mathcal {R}$ be a finite ring, and let $A \subseteq \mathcal {R}$ be a set, $|A| = \alpha |\mathcal {R}|$ . Then

$$\begin{align*}\mathrm{cov}^\times (2A-2A) \leqslant \alpha^{-1} , \end{align*}$$

provided all numbers $1,\dots , [\alpha ^{-1}]$ belong to $\mathcal {R}^*$ .

Using the same method, one can estimate the multiplicative covering number of a Bohr set in ${\mathbb {Z}}_p$ (p is a prime number):

$$\begin{align*}\mathcal{B} (\Gamma, \varepsilon) = \{ x\in {\mathbb{Z}}_p ~:~ \| x\gamma/p\| \leqslant \varepsilon,\, \forall \gamma \in \Gamma \} \quad \varepsilon \in (0,1],\, \quad \Gamma \subseteq {\mathbb{Z}}_p , \end{align*}$$

namely, we have

$$\begin{align*}\mathrm{cov}^{\times} (\mathcal{B} (\Gamma, \varepsilon)) \leqslant \varepsilon^{-|\Gamma|} . \end{align*}$$

It is interesting to decrease the number of summands in Corollary 5.3. To this end, let us obtain the main result of this section.

Theorem 5.4 Let q be a positive integer, let $A \subseteq {\mathbb {Z}}_q$ be a set, $|A| = \alpha q$ . Suppose that the least prime factor of q greater than $2 \alpha ^{-1}+3$ . Then

(5.3) $$ \begin{align} \mathrm{cov}^\times (A-A) \leqslant \frac{1}{\alpha} + 1 . \end{align} $$

More concretely, $[k_*]^{-1} \cdot (A-A) = {\mathbb {Z}}_q$ for a certain $k_* \leqslant \alpha ^{-1}+1$ .

Proof Let $p_1$ be the least prime factor of q. By our assumption, we know that ${p_1 \geqslant 2 \alpha ^{-1}+3}$ . Write $p_1=2k+1$ and take $\Lambda = \{0,1,\dots , k_*\}$ , where $\lceil \alpha ^{-1} - 1 \rceil + 1 = k_* \leqslant k$ . Then one has $Y:= (\Lambda - \Lambda )\setminus \{0\} \subseteq {\mathbb {Z}}^*_q$ . First of all, consider $n\in {\mathbb {Z}}_q^*$ and form the set $n\cdot \Lambda + A$ . Since $|\Lambda ||A| = (k_* +1) \alpha q> q$ , it follows that there are different $\lambda _1,\lambda _2 \in \Lambda $ such that

$$\begin{align*}n\lambda_1 + a_1 \equiv n\lambda_2 + a_2\quad \pmod q , \end{align*}$$

where $a_1, a_2 \in A$ and $a_1 \neq a_2$ . Hence $n\in Y^{-1} (A-A)$ and thus ${\mathbb {Z}}_q^* \subseteq Y^{-1} (A-A)$ . Also, notice that as in Proposition 5.2, one has $Y^{-1} (A-A) = [k_*]^{-1} \cdot (A-A)$ .

Now, let $n=n' q_1$ , where $q_1|q$ and $n'$ is coprime to q. By the pigeonhole principle, there is $B \subseteq {\mathbb {Z}}_{q/q_1}$ and $s\in {\mathbb {Z}}_q$ such that $q_1 B+s \subseteq A$ and the density of B in ${\mathbb {Z}}_{q/q_1}$ is at least $\alpha $ . In particular, we have $q_1 (B-B) \subseteq A-A$ . By the same argument as above, one has $n' \equiv y^{-1} (b_1-b_2) \pmod {q/q_1}$ , where $y\in Y$ and $b_1,b_2 \in B$ . It follows that ${n \equiv y^{-1} (a_1-a_2) \pmod q}$ as required. Thus, we have proved that $[k_*]^{-1} (A-A) = {\mathbb {Z}}_q,$ and hence $\mathrm {cov}^\times (A-A) \leqslant k_* \leqslant \alpha ^{-1}+1$ . This completes the proof.

Remark 5.5 After the paper was written, the author was informed by Fish that Theorem 5.4 holds in greater generality, namely, for any measure preserving system the same is true for the set of return times of a set of positive measure.

Theorem 5.4 implies a consequence about the multiplicative covering numbers of the intersections of difference sets in the spirit of paper [20] (see [20, Theorems 1 and 3]).

Corollary 5.6 Let q be a positive integer, and let $A_1,\dots , A_k \subseteq {\mathbb {Z}}_q$ be sets, $|A_i| = \alpha _i q$ , $i\in [k]$ . Suppose that the least prime factor of q greater than $2 (\alpha _1, \dots , \alpha _k)^{-1}+3$ . Then

(5.4) $$ \begin{align} \mathrm{cov}^{\times} \left(\bigcap_{i=1}^k (A_i - A_i) \right) \leqslant \frac{1}{\alpha_1, \dots, \alpha_k} + 1 . \end{align} $$

Proof Put $A_{\vec {s}} = A_1 \cap (A_2-s_1) \cap \dots (A_k-s_{k-1})$ , where $\vec {s} = (s_1,\dots , s_{k-1}) \in {\mathbb {Z}}^{k-1}_q$ . We have $\sum _{\vec {s}} |A_{\vec {s}}| = |A_1| \dots |A_k|$ , and hence, there is $\vec {s}_*$ such that $|A_{\vec {s}_*}| \geqslant \alpha _1, \dots , \alpha _k q$ . Clearly, for any $\vec {s}$ , one has

$$\begin{align*}A_{\vec{s}} - A_{\vec{s}} \subseteq \bigcap_{i=1}^k (A_i - A_i) . \end{align*}$$

Applying Theorem 5.4 with $A = A_{\vec {s}_*}$ , we obtain bound (5.4). This completes the proof.

As we have seen before, Corollary 5.3 and Theorem 5.4 give us some bounds for the multiplicative covering numbers of difference sets. On the other hand, one can see that Theorem 5.4 does not hold for, say, nonzero shifts of Bohr sets, for the sumsets $A+A$ , for the higher sumsets $nA$ , $n>2$ and so on. Indeed, consider the following.

Example 5.7 Let p be a prime number and $S = [p/3,2p/3)$ or $S=\pm [p/6,p/3)$ to make S symmetric. Then the equation $a+b \equiv c\quad \pmod p$ has no solutions in $a,b,c\in S$ . Further, we have $|S| \gg p$ but it is easy to see that $\mathrm {cov}^\times (S)$ is unbounded. Indeed, if $SX = {\mathbb {Z}}_p$ for a set X with $|X| = O(1)$ , then we obtain a coloring of ${\mathbb {Z}}_p$ with a finite number of colors and every color has no solutions to our equation $a+b \equiv c\quad \pmod p$ . It gives us a contradiction with the famous Schur theorem, (see [14]) (actually, it implies $\mathrm {cov}^\times (S) \gg \log p/\log \log p$ ).

In particular, we see that $\mathrm {cov}^\times (X+s)$ can be much larger than $\mathrm {cov}^\times (X)$ for a set X and a nonzero s.

Proposition 5.2 implies that any syndetic set $S\subseteq \mathbb {F}_p$ , $|S| \gg p$ has ${\mathrm {cov}^{\times } (S-S) = O(1)}$ . On the other hand, thanks to inclusion (5.2) any set of the form $A-A$ , where $A\subseteq \mathbb {F}_p$ , $|A| \gg p$ is syndetic (with the gap depending on A but not just on $p/|A|$ , of course). Thus, it is natural to ask about a generalization of Theorem 5.4 to the family of syndetic sets. Nevertheless, taking $S=\{ 1+ kM\}_{k\in [(p-1)/M]}$ , $M\geqslant 5$ and $p \equiv 2 \pmod M$ , say, we see that S is a syndetic set and S has no solutions to the equation $a+b \equiv c \pmod p$ . Thus, as in the example above, we see that $\mathrm {cov}^\times (S)$ is unbounded.

Remark 5.8 A dual form of Theorem 5.4 has no place, namely, there is a set ${A\subseteq {\mathbb {Z}}_p}$ , $|A| \gg p$ such that $\mathrm {cov}^{+} (A/A) \gg \log p$ . In other words, $\mathrm {cov}^{+} (A/A)$ is close to the maximal possible value. To see this, just take A to be the set of all quadratic residues (see, e.g., [13, Proposition 14]).

Finally, let us give another proof of a variant of Theorem 1.1 via our covering Theorem 5.4. Notice that the number d below can be a non-divisor of q.

Theorem 5.9 Let q be a positive integer, let $A, B\subset {\mathbb {Z}}_q$ be sets, $|A| = \alpha q$ , $|B|=\beta q$ , and let us assume that $\alpha \geqslant \beta $ . Suppose that the least prime factor of q greater than $2 \beta ^{-1}+3$ . Then, there is $d\neq 0$ with

(5.5) $$ \begin{align} d \leqslant \alpha^{-\beta^{-1} -1} , \end{align} $$

and such that

(5.6) $$ \begin{align} d \cdot {\mathbb{Z}}_q \subseteq (A-A)(B-B) . \end{align} $$

Proof Applying Theorem 5.4 with $A=B$ , we find a set $X\subseteq {\mathbb {Z}}_q$ , $n:=|X| \leqslant \beta ^{-1} +1$ such that $X(B-B) = {\mathbb {Z}}_q$ . Let $X = \{ x_1,\dots ,x_n\}$ and $\vec {x} = (x_1,\dots ,x_n) \in {\mathbb {Z}}^n_q$ . Considering the collection of the sets $A^n + j \cdot \vec {x} \subseteq {\mathbb {Z}}^n_q$ , $j\geqslant 1$ , we see that there is $0<d \leqslant \alpha ^{-n}$ with $d\cdot X \subseteq A-A$ . Hence

$$\begin{align*}(A-A)(B-B) \supseteq d\cdot X (B-B) \supseteq d \cdot {\mathbb{Z}}_q \end{align*}$$

as required. It remains to notice that

$$\begin{align*}d \leqslant \alpha^{-n} \leqslant \alpha^{-\beta^{-1} -1} . \end{align*}$$

This completes the proof.

6 Concluding remarks

Let us discuss other approaches to Theorem 1.1. First of all, recall the well-known Furstenberg’s result [6].

Theorem 6.1 [Furstenberg]. Let n be a positive integer, let $\delta \in (0,1]$ be a real number, and let S be a set of size n. Then for all sufficiently large $N \geqslant N(\delta ,n)$ an arbitrary set $A\subseteq [N]\times [N]$ , $|A| \geqslant \delta N^2$ contains the set $\alpha +\beta \cdot S$ for some $\alpha $ and $\beta \neq 0$ .

Quantitative bounds for $N(\delta ,n)$ from Theorem 6.1 can be found in [15].

Corollary 6.2 Let q be a prime number, $\mathcal {A} \subseteq \mathbb {F}^2_q$ , $|\mathcal {A}| = \delta q^2$ and $A,B \subseteq \mathbb {F}_q$ , $|A| = \alpha _* q$ , $|B| = \beta _* q$ . Then, there is a decreasing positive function $\varphi $ such that if $\min \{\alpha _*,\beta _*,\delta \} \geqslant \varphi (q)$ , then formula (3.1) takes place for $\mathcal {B} = A\times B$ , any $\lambda \in {\mathbb {Z}}^*_q$ and $d=1$ .

Proof Take $S=S_1=[k]\times [k]$ or $S=S_2 = \{ (2j,2j) ~:~ j\in [k]\}$ for a certain positive integer k. Applying Theorem 6.1 with $n=|S|$ and $A=\mathcal {A}$ , we see that for some $\alpha $ , $\beta \neq 0$ the following holds $\alpha +\beta \cdot S \subseteq \mathcal {A}$ and hence to solve (3.1) with $d=1$ it is sufficiently to find for any $\lambda \in {\mathbb {Z}}^*_q$ some elements $a\in \beta ^{-1} (A-\alpha )$ , $b\in \beta ^{-1} (B-\alpha )$ and $(t_1,t_2) \in S$ such that

$$\begin{align*}(t_1 - a) (t_2-b) \equiv \lambda \pmod q . \end{align*}$$

If for a certain absolute constant $C>0$ , one has $k \gg \min ^{-C} \{\alpha _* ,\beta _*,\delta \}$ , then for ${S=S_2}$ , the last equation has a solution thanks to the famous Bourgain–Gamburd machine [4] (see details in [18], say) and for $S=S_1$ (actually, for any dense subset of $S_1$ ), the latter fact was obtained in [18, Theorem 3]. This completes the proof.

The author does not know how to obtain Corollary 6.2 for composite q because there is no control over divisors of $\beta $ in Theorem 6.1. It would be interesting to say something about prime factors of the dilation $\beta $ .

We finish this section with a problem (it is interesting in its own right from a combinatorial point of view), which potentially gives another proof of Corollary 6.2 thanks to [18, Theorem 3].

Problem 6.3 Let n be a positive integer, and let $\delta ,\kappa \in (0,1]$ be real numbers. Then for all sufficiently large $N\geqslant N(\delta ,\kappa ,n)$ an arbitrary set $A\subseteq [N]\times [N]$ , $|A| \geqslant \delta N^2$ contains the set $\alpha +\beta \cdot S$ for some $\alpha $ and $\beta $ , where $S \subseteq [n]\times [n]$ is any set of size $n^{1+\kappa }$ .

Of course, some estimates on $N(\delta ,\kappa ,n)$ follow from Theorem 6.1 but maybe it is possible to obtain a better bound.