Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T20:32:24.606Z Has data issue: false hasContentIssue false
  • English
  • Français

On Some 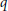$q$-Analogs of a Theorem of Kostant-Rallis

Published online by Cambridge University Press:  20 November 2018

N. R. Wallach  and
J. Willenbring
N. R. Wallach
Affiliation:
Department of Mathematics, University of California, San Diego, La Jolla, CA 92093, USA email: nwallach@ucsd.edu, jwilleb@math.ucsd.edu
J. Willenbring
Affiliation:
Department of Mathematics, University of California, San Diego, La Jolla, CA 92093, USA email: nwallach@ucsd.edu, jwilleb@math.ucsd.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the first part of this paper generalizations of Hesselink’s 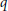$q$-analog of Kostant’smultiplicity formula for the action of a semisimple Lie group on the polynomials on its Lie algebra are given in the context of the Kostant-Rallis theorem. They correspond to the cases of real semisimple Lie groups with one conjugacy class of Cartan subgroup. In the second part of the paper a 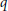$q$-analog of the Kostant-Rallis theorem is given for the real group 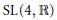$\text{SL(4,}\,\mathbb{R}\text{)}$ (that is 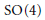$\text{SO}(4)$ acting on symmetric 4 × 4 matrices). This example plays two roles. First it contrasts with the examples of the first part. Second it has implications to the study of entanglement of mixed 2 qubit states in quantum computation.

Keywords

22E4720G05
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 52 , Issue 2 , 01 April 2000 , pp. 438 - 448
Copyright
Copyright © Canadian Mathematical Society 2000

References

[Chev] Chevalley, C., Sur certains groupes simples. Tôhoku Math. J. 7(1955), 14–66.Google Scholar
[G-W] Goodman, R. and Wallach, N., Representations and invariants of the classical groups. CambridgeUniversity Press, Cambridge, 1998.Google Scholar
[Hess] Hesselink, W. H., Characters of the null cone. Math. Ann. 252(1982), 179–182.Google Scholar
[K] Kostant, B., Lie group representations in polynomial rings. Amer. J. Math. 85(1963), 327–387.Google Scholar
[K-R] Kostant, B. and Rallis, S., Orbits and Lie group representations associated with symmetric spaces. Amer. J. Math. 93(1971), 753–809.Google Scholar