Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Flajolet, Philippe
and
Steyaert, Jean-Marc
1980.
Automata, Languages and Programming.
Vol. 85,
Issue. ,
p.
208.
Grimmett, G. R.
1980.
Random labelled trees and their branching networks.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 30,
Issue. 2,
p.
229.
Flajolet, Philippe
and
Odlyzko, Andrew
1980.
Exploring binary trees and other simple trees.
p.
207.
Meir, A.
and
Moon, J. W.
1981.
Terminal path numbers for certain families of trees.
Journal of the Australian Mathematical Society,
Vol. 31,
Issue. 4,
p.
429.
Dershowitz, Nachum
and
Zaks, Shmuel
1981.
CAAP '81.
Vol. 112,
Issue. ,
p.
180.
Capobianco, Michael
1981.
Statistical Distributions in Scientific Work.
p.
397.
Flajolet, Philippe
and
Steyaert, Jean-Marc
1981.
A complexity calculus for classes of recursive search programs over tree structures.
p.
386.
Meir, A.
and
Moon, J. W.
1981.
The outer-distance of nodes in random trees.
Aequationes Mathematicae,
Vol. 23,
Issue. 1,
p.
204.
Flajolet, Philippe
and
Odlyzko, Andrew
1982.
The average height of binary trees and other simple trees.
Journal of Computer and System Sciences,
Vol. 25,
Issue. 2,
p.
171.
Karoński, Michał
1982.
A review of random graphs.
Journal of Graph Theory,
Vol. 6,
Issue. 4,
p.
349.
Kirschenhofer, Peter
and
Prodinger, Helmut
1982.
On the average hyperoscillations of planted plane trees.
Combinatorica,
Vol. 2,
Issue. 2,
p.
177.
Kemp, R.
1982.
Theoretical Computer Science.
Vol. 145,
Issue. ,
p.
153.
Kirschenhofer, Peter
1983.
On the average shape of simply generated families of trees.
Journal of Graph Theory,
Vol. 7,
Issue. 3,
p.
311.
Wang, Zhenyu
1983.
ADDITIVE ENUMERATION PROBLEMS OVER TREES.
Acta Mathematica Scientia,
Vol. 3,
Issue. 4,
p.
445.
Steyaert, Jean-Marc
and
Flajolet, Philippe
1983.
Patterns and pattern-matching in trees: An analysis.
Information and Control,
Vol. 58,
Issue. 1-3,
p.
19.
Jamison, Robert E
1983.
On the average number of nodes in a subtree of a tree.
Journal of Combinatorial Theory, Series B,
Vol. 35,
Issue. 3,
p.
207.
Kirschenhofer, Peter
Prodinger, Helmut
and
Tichy, Robert F.
1983.
Fibonacci Numbers of Graphs: II.
The Fibonacci Quarterly,
Vol. 21,
Issue. 3,
p.
219.
Kirschenhofer, Peter
1984.
On the average shape of monotonically labelled tree structures.
Discrete Applied Mathematics,
Vol. 7,
Issue. 2,
p.
161.
Kemp, R.
1984.
STACS 84.
Vol. 166,
Issue. ,
p.
109.
Prodinger, Helmut
1984.
On the altitude of specified nodes in random trees.
Journal of Graph Theory,
Vol. 8,
Issue. 4,
p.
481.


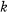 is the number
is the number 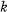 in
in 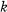 = 0, 1, …
= 0, 1, …