Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T17:00:09.206Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Behavior of Zeros of Polynomials of Best and Near-Best Approximation

Published online by Cambridge University Press:  20 November 2018

K. G. Ivanov ,
E. B. Saff  and
V. Totik
K. G. Ivanov
Affiliation:
Institute of Mathematics, Bulgarian Academy of Science, Sofia, 1090 Bulgaria
E. B. Saff
Affiliation:
Institute for Constructive Mathematics, Department of Mathematics, University of South Florida, Tampa, Florida 33620, USA
V. Totik
Affiliation:
Bolyai Institute, Aradi V. tere 1, Szeged, 6720 Hungary Department of Mathematics, University of South Florida, Tampa, Florida 33620, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Assume ƒ is continuous on the closed disk D1 : |z| ≤ 1, analytic in |z| ≤ 1, but not analytic on D1. Our concern is with the behavior of the zeros of the polynomials 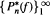of best uniform approximation to ƒ on D1. It is known that, for such ƒ, every point of the circle |z| = 1 is a cluster point of the set of all zeros of 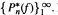Here we show that this property need not hold for every subsequence of the 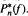Specifically, there exists such an f for which the zeros of a suitable subsequence 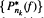all tend to infinity. Further, for near-best polynomial approximants, we show that this behavior can occur for the whole sequence. Our examples can be modified to apply to approximation in the Lq-norm on |z|= 1 and to uniform approximation on general planar sets (including real intervals).

Keywords

41A20
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 43 , Issue 5 , 01 October 1991 , pp. 1010 - 1021
Copyright
Copyright © Canadian Mathematical Society 1991

References

1. Blatt, H.-P. and Saff, E.B., Behavior of zeros of polynomials of near best approximation, J. Approx. Theory 46 (1986),323–344.Google Scholar
2. Blatt, H.-P., Saff, E.B. and Simkani, M., Jentzsch-Szeg ő type theorems for the zeros of best approximants, J. London Math. Soc. 38 (1988), 307–316.Google Scholar
3. Feinerman, R.P. and Newman, D.J., Polynomial approximation. The Williams & Wilkins Company, Baltimore, 1974.Google Scholar
4. Grothmann, R. and Saff, E.B., On the behavior of zeros and poles of best uniform polynomial and rational approximation. In: Nonlinear Numerical Methods and Rational Approximations, (A. Cuyt, éd.), Reidel Publishing Company, 1988, 1988–57.Google Scholar
5. Hille, E., Analytic function theory, vol. II. Ginn and Company, Boston, 1962.Google Scholar
6. Jentzsch, R., Untersuchungen zur Théorie Analytischer Funktionen. Inaugural-dissertation, Berlin, 1914.Google Scholar
7. Jentzsch, R., Fortgesetzte Untersuchungen iiber die Abschnitte von Potenzreihen, Acta Math. 41 (1918), 253- 270.Google Scholar
8. Saff, E.B., A principle of contamination in best polynomial approximation. In: Approximation and Optimization (Gomez et al., eds.), Lecture Notes in Math., 1354, Springer-Verlag, Heidelberg, 1988,79–97.Google Scholar
9. Timan, A.F., Theory of approximation of functions of a real variable. Pergamon Press, New York, 1963.Google Scholar
10. Walsh, J.L., Interpolation and approximation by rational functions in the complex domain. AMS Colloquium Publications, XX, third edition, Amer. Math. Soc, Providence, 1960.Google Scholar