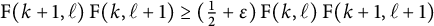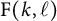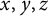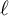1 Introduction
This paper is centered around the cross-product conjecture (CPP) by Brightwell, Felsner, and Trotter that gives the best-known bound for the celebrated
![]() $\frac {1}{3}$
–
$\frac {1}{3}$
–
![]() $\frac {2}{3}$
Conjecture [Reference Brightwell, Felsner and TrotterBFT95, Theorem 1.3]. Here, we prove several weak versions of the conjecture, and disprove a stronger version we conjectured earlier in [Reference Chan, Pak and PanovaCPP22].
$\frac {2}{3}$
Conjecture [Reference Brightwell, Felsner and TrotterBFT95, Theorem 1.3]. Here, we prove several weak versions of the conjecture, and disprove a stronger version we conjectured earlier in [Reference Chan, Pak and PanovaCPP22].
Let
![]() $P=(X,\prec )$
be a poset with
$P=(X,\prec )$
be a poset with
![]() $|X|=n$
elements. A linear extension of P is a bijection
$|X|=n$
elements. A linear extension of P is a bijection
![]() $L: X \to [n]=\{1,\ldots ,n\}$
, such that
$L: X \to [n]=\{1,\ldots ,n\}$
, such that
![]() $L(x) < L(y)$
for all
$L(x) < L(y)$
for all
![]() $x \prec y$
. Denote by
$x \prec y$
. Denote by
![]() $\mathcal {E}(P)$
the set of linear extensions of P. Fix distinct elements
$\mathcal {E}(P)$
the set of linear extensions of P. Fix distinct elements
![]() $x,y,z\in X$
. For
$x,y,z\in X$
. For
![]() $k,\ell \geq 1$
, let
$k,\ell \geq 1$
, let
and let
![]() $\textrm {F}(k,\ell ) \hskip .06cm := \hskip .06cm \big |\mathcal F(k,\ell )\big |$
.
$\textrm {F}(k,\ell ) \hskip .06cm := \hskip .06cm \big |\mathcal F(k,\ell )\big |$
.
Conjecture 1.1 (Cross-product conjecture [Reference Brightwell, Felsner and TrotterBFT95, Conjecture 3.1])
We have
The CPC was proved in [Reference Brightwell, Felsner and TrotterBFT95, Theorem 3.2] for
![]() $k=\ell =1$
, and in [Reference Chan, Pak and PanovaCPP22, Theorem 1.4] for posets of width 2. We also show in [Reference Chan, Pak and PanovaCPP22, Section 3] that both the Kahn–Saks and the Graham–Yao–Yao inequalities follow from (CPC).
$k=\ell =1$
, and in [Reference Chan, Pak and PanovaCPP22, Theorem 1.4] for posets of width 2. We also show in [Reference Chan, Pak and PanovaCPP22, Section 3] that both the Kahn–Saks and the Graham–Yao–Yao inequalities follow from (CPC).
Theorem 1.2 (Main theorem)
Let
![]() $P=(X,\prec )$
be a poset on
$P=(X,\prec )$
be a poset on
![]() $|X|=n$
elements. Fix distinct elements
$|X|=n$
elements. Fix distinct elements
![]() $x,y,z\in X$
. Suppose that
$x,y,z\in X$
. Suppose that
![]() $\mathrm {F}(k,\ell +2)\hskip .06cm\mathrm {F}(k+2,\ell )> 0$
. Then,
$\mathrm {F}(k,\ell +2)\hskip .06cm\mathrm {F}(k+2,\ell )> 0$
. Then,
Suppose that
![]() $\textrm {F}(k,\ell +2)=0$
and
$\textrm {F}(k,\ell +2)=0$
and
![]() $\textrm {F}(k+2,\ell )> 0$
. Then,
$\textrm {F}(k+2,\ell )> 0$
. Then,
Suppose that
![]() $\textrm {F}(k+2,\ell )=0$
and
$\textrm {F}(k+2,\ell )=0$
and
![]() $\textrm {F}(k,\ell +2)> 0$
. Then,
$\textrm {F}(k,\ell +2)> 0$
. Then,
Finally, suppose that
![]() $\textrm {F}(k,\ell +2) \hskip .03cm = \hskip .03cm \textrm {F}(k+2,\ell ) = 0$
and
$\textrm {F}(k,\ell +2) \hskip .03cm = \hskip .03cm \textrm {F}(k+2,\ell ) = 0$
and
![]() $\textrm {F}(k,\ell )\hskip .06cm \mathrm {F}(k+1,\ell +1)>0$
. Then,
$\textrm {F}(k,\ell )\hskip .06cm \mathrm {F}(k+1,\ell +1)>0$
. Then,
When
![]() $\textrm {F}(k,\ell )\hskip .06cm \textrm {F}(k+1,\ell +1)=0$
, the inequality (CPC) holds trivially. Curiously, the equality (1.4) does not hold in that case since the LHS can be strictly positive (Example 4.5). Except for the natural symmetry between (1.3) and (1.2), the proof of remaining three cases are quite different and occupies much of the paper.
$\textrm {F}(k,\ell )\hskip .06cm \textrm {F}(k+1,\ell +1)=0$
, the inequality (CPC) holds trivially. Curiously, the equality (1.4) does not hold in that case since the LHS can be strictly positive (Example 4.5). Except for the natural symmetry between (1.3) and (1.2), the proof of remaining three cases are quite different and occupies much of the paper.
Note that computing the number
![]() $e(P)$
of linear extensions of P is
$e(P)$
of linear extensions of P is ![]() -complete [Reference Brightwell and WinklerBW91], even for posets of height 2 or dimension 2 [Reference Dittmer and PakDP18]. Still, the vanishing assumptions which distinguish the cases in the Main Theorem 1.2 can be decided in polynomial time (see Theorem 4.2).
-complete [Reference Brightwell and WinklerBW91], even for posets of height 2 or dimension 2 [Reference Dittmer and PakDP18]. Still, the vanishing assumptions which distinguish the cases in the Main Theorem 1.2 can be decided in polynomial time (see Theorem 4.2).
The proof of the Main Theorem 1.2 is a combination of geometric and combinatorial arguments. The former are fairly standard in the area, and used largely as a black box. The combinatorial part is where the paper becomes technical, as the translation of geometric ratios into the language of posets (following Stanley’s pioneering approach in [Reference StanleySta81]) leads to bounds on ratios of linear extensions that have not been investigated until now. Here, we employ the combinatorics of words technology following our previous work [Reference Chan, Pak and PanovaCPP22, Reference Chan, Pak and PanovaCPP23a, Reference Chan, Pak and PanovaCPP23b] (cf. Section 8.7)
Let us emphasize that getting an explicit constant above
![]() $\frac 12$
in the RHS is the main difficulty in the proof, as the
$\frac 12$
in the RHS is the main difficulty in the proof, as the
![]() $\frac 12$
constant is relatively straightforward to obtain from Favard’s inequality. This was noticed independently by Yair Shenfeld who derived it from Theorem 2.4 in the same way we did in the proof of Theorem 3.1.Footnote
1
In another independent development, Julius Ross, Hendrik Süss, and Thomas Wannerer gave a proof of the same
$\frac 12$
constant is relatively straightforward to obtain from Favard’s inequality. This was noticed independently by Yair Shenfeld who derived it from Theorem 2.4 in the same way we did in the proof of Theorem 3.1.Footnote
1
In another independent development, Julius Ross, Hendrik Süss, and Thomas Wannerer gave a proof of the same
![]() $\frac 12$
lower bound using the technology of Lorentzian polynomials [Reference Brändén and HuhBH20] combined with a technical result from [Reference Brändén, Leake and PakBLP23].Footnote
2
$\frac 12$
lower bound using the technology of Lorentzian polynomials [Reference Brändén and HuhBH20] combined with a technical result from [Reference Brändén, Leake and PakBLP23].Footnote
2
Our combinatorial tools also allow us to inch closer to the CPC for two classes of posets. Fix a subset
![]() $A\subseteq X$
. We say that a poset
$A\subseteq X$
. We say that a poset
![]() $P=(X,\prec )$
is
t-thin with respect to A
, if for every
$P=(X,\prec )$
is
t-thin with respect to A
, if for every
![]() $u \in X\smallsetminus A$
there are at most t elements incomparable to
$u \in X\smallsetminus A$
there are at most t elements incomparable to
![]() $\hskip .03cm u$
. For
$\hskip .03cm u$
. For
![]() $A=\varnothing $
, such posets are a subclass of posets of width t. This class is a generalization of t-thin posets (the case of
$A=\varnothing $
, such posets are a subclass of posets of width t. This class is a generalization of t-thin posets (the case of
![]() $A=X$
), studied in the context of the
$A=X$
), studied in the context of the
![]() $\frac {1}{3}$
–
$\frac {1}{3}$
–
![]() $\frac {2}{3}$
Conjecture [Reference Brightwell and WrightBW92, Reference PeczarskiPec08].
$\frac {2}{3}$
Conjecture [Reference Brightwell and WrightBW92, Reference PeczarskiPec08].
Similarly, we say that a poset
![]() $P=(X,\prec )$
is
t-flat with respect to A
, if for every
$P=(X,\prec )$
is
t-flat with respect to A
, if for every
![]() $u \in A$
there are at most t elements comparable to u. For
$u \in A$
there are at most t elements comparable to u. For
![]() $A=X$
, such posets are a subclass of posets of height t. Examples include incidence posets (see, e.g., [Reference TrotterTro95, Section 10]), defined as follows. Let
$A=X$
, such posets are a subclass of posets of height t. Examples include incidence posets (see, e.g., [Reference TrotterTro95, Section 10]), defined as follows. Let
![]() $G=(V,E)$
be a simple graph, let
$G=(V,E)$
be a simple graph, let
![]() $X=V\cup E$
, and let
$X=V\cup E$
, and let
![]() $v\prec e$
for all
$v\prec e$
for all
![]() $e=(v,w)\in E$
. For
$e=(v,w)\in E$
. For
![]() $A\subseteq E$
, the corresponding poset P is
$A\subseteq E$
, the corresponding poset P is
![]() $2$
-flat with respect to A. For
$2$
-flat with respect to A. For
![]() $A\subseteq V$
and G is d-regular, the corresponding poset P is d-flat with respect to A.
$A\subseteq V$
and G is d-regular, the corresponding poset P is d-flat with respect to A.
Theorem 1.3 Let
![]() $P=(X,\prec )$
be a finite poset. Fix distinct elements
$P=(X,\prec )$
be a finite poset. Fix distinct elements
![]() $x,y,z\in X$
, and let
$x,y,z\in X$
, and let
![]() $A:=\{x,y,z\}$
. Suppose that P is either t-thin with respect to A, or t-flat with respect to A. Then,
$A:=\{x,y,z\}$
. Suppose that P is either t-thin with respect to A, or t-flat with respect to A. Then,
Note that the constant in the RHS of (1.5) depends only on t, and thus holds for posets of arbitrary large size n (see also Section 8.3). We also have the following counterpart to the CPC.
Theorem 1.4 (Converse cross-product inequality)
Suppose that
![]() $\textrm {F}(k,\ell ) \textrm {F}(k+1, \ell +1)>0$
. Then,
$\textrm {F}(k,\ell ) \textrm {F}(k+1, \ell +1)>0$
. Then,
Note that the inequality in the theorem is asymptotically tight (see Proposition 7.5). On the other hand, originally we believed in the following stronger version of the CPC:
Conjecture 1.5 (Generalized cross-product conjecture [Reference Chan, Pak and PanovaCPP22, Conjecture 3.2])
We have
For
![]() $p=k+1$
and
$p=k+1$
and
![]() $q=\ell +1$
, where
$q=\ell +1$
, where
![]() $k,\ell \geq 1$
, this gives (CPC). In [Reference Chan, Pak and PanovaCPP22, Theorem 3.3], the inequality (GCPC) was proved for posets of width 2. However, here we show that it fails in full generality.
$k,\ell \geq 1$
, this gives (CPC). In [Reference Chan, Pak and PanovaCPP22, Theorem 3.3], the inequality (GCPC) was proved for posets of width 2. However, here we show that it fails in full generality.
Theorem 1.6 The inequality (GCPC) fails for an infinite family of posets of width 3.
Our final result further confirms that CPC is somehow special among similar families of inequalities. While these other inequalities are not always true, they are not simultaneously too far off in the following sense.
Theorem 1.7 For every
![]() $P=(X,\prec )$
, every distinct
$P=(X,\prec )$
, every distinct
![]() $x,y,z\in X$
, and every
$x,y,z\in X$
, and every
![]() $k,\ell \ge 1$
, at least two of the inequalities (CPC), (CPC1), and (CPC2) are true, where
$k,\ell \ge 1$
, at least two of the inequalities (CPC), (CPC1), and (CPC2) are true, where
We prove that inequalities (CPC1) and (CPC2) hold for posets of width 2 (Corollary 7.3). However, they are false on infinite families of counterexamples (Proposition 7.1). By Theorem 1.7, this means that the CPC holds in all these cases.
Paper structure
We start with a short background Section 2 on mixed volumes and variations on the Alexandrov–Fenchel inequalities. This section is self-contained in presentation, and uses several well-known results as a black box. In a lengthy Section 3, we show how cross-product inequalities arise as mixed volume, and make some useful calculations. We also prove Theorem 1.7.
We begin our combinatorial study of linear extensions in Section 4, where we give explicit conditions for vanishing of
![]() $\textrm {F}(k,\ell )$
, and explore the consequences which include the equality (1.4). In Sections 5 and 6, we prove different cross-product inequalities in the nonvanishing and vanishing case, respectively. We conclude with explicit examples (Section 7) and final remarks (Section 8).
$\textrm {F}(k,\ell )$
, and explore the consequences which include the equality (1.4). In Sections 5 and 6, we prove different cross-product inequalities in the nonvanishing and vanishing case, respectively. We conclude with explicit examples (Section 7) and final remarks (Section 8).
2 Mixed volume inequalities
2.1 Alexandrov–Fenchel inequalities
Fix
![]() $n \geq 1$
. For two sets
$n \geq 1$
. For two sets
![]() $A, B \subset \mathbb {R}^n$
and constants
$A, B \subset \mathbb {R}^n$
and constants
![]() $a,b>0$
, denote by
$a,b>0$
, denote by
the Minkowski sum of these sets. For a convex body
![]() $\mathrm {A} \subset \mathbb {R}^n$
with affine dimension d, denote by
$\mathrm {A} \subset \mathbb {R}^n$
with affine dimension d, denote by
![]() $\mathrm {Vol}_d(\mathrm {A})$
the volume of
$\mathrm {Vol}_d(\mathrm {A})$
the volume of
![]() $\mathrm {A}$
. One of the basic results in convex geometry is Minkowski’s theorem that the volume of convex bodies with affine dimension d behaves as a homogeneous polynomial of degree d with nonnegative coefficients.
$\mathrm {A}$
. One of the basic results in convex geometry is Minkowski’s theorem that the volume of convex bodies with affine dimension d behaves as a homogeneous polynomial of degree d with nonnegative coefficients.
Theorem 2.1 (Minkowski; see, e.g., [Reference Burago and ZalgallerBuZ88, Section 19.1])
For all convex bodies
![]() $\mathrm {A}_1, \ldots , \mathrm {A}_r \subset \mathbb {R}^n$
and
$\mathrm {A}_1, \ldots , \mathrm {A}_r \subset \mathbb {R}^n$
and
![]() $\lambda _1,\ldots , \lambda _r> 0$
, we have
$\lambda _1,\ldots , \lambda _r> 0$
, we have
where the functions
![]() $\mathrm {V}(\cdot )$
are nonnegative and symmetric, and where d is the affine dimension of
$\mathrm {V}(\cdot )$
are nonnegative and symmetric, and where d is the affine dimension of
![]() $\lambda _1 \mathrm {A}_1+ \cdots + \lambda _r \mathrm {A}_r$
$\lambda _1 \mathrm {A}_1+ \cdots + \lambda _r \mathrm {A}_r$
![]() $($
which does not depend on the choice of
$($
which does not depend on the choice of
![]() $\lambda _1,\ldots , \lambda _r)$
.
$\lambda _1,\ldots , \lambda _r)$
.
The coefficients
![]() $\mathrm {V}(\mathrm {A}_{i_1},\ldots , \mathrm {A}_{i_d})$
are called mixed volumes of
$\mathrm {V}(\mathrm {A}_{i_1},\ldots , \mathrm {A}_{i_d})$
are called mixed volumes of
![]() $\mathrm {A}_{i_1}, \ldots , \mathrm {A}_{i_d}$
. We use
$\mathrm {A}_{i_1}, \ldots , \mathrm {A}_{i_d}$
. We use
![]() $d:=d(\mathrm {A}_1,\ldots , \mathrm {A}_r)$
to denote the affine dimension of the Minkowski sum
$d:=d(\mathrm {A}_1,\ldots , \mathrm {A}_r)$
to denote the affine dimension of the Minkowski sum
![]() $\mathrm {A}_1+\cdots +\mathrm {A}_r$
.
$\mathrm {A}_1+\cdots +\mathrm {A}_r$
.
There are many classical inequalities concerning mixed volumes, and here we list those that will be used in this paper. Let
![]() $\mathrm {A},\mathrm {B},\mathrm {C}$
,
$\mathrm {A},\mathrm {B},\mathrm {C}$
,
![]() $\mathrm {Q}_1,\ldots , \mathrm {Q}_{d-2}$
be convex bodies in
$\mathrm {Q}_1,\ldots , \mathrm {Q}_{d-2}$
be convex bodies in
![]() $\mathbb {R}^n$
. We denote
$\mathbb {R}^n$
. We denote
![]() ${\textbf {Q}}=(\mathrm {Q}_1,\ldots ,\mathrm {Q}_{d-2})$
and use
${\textbf {Q}}=(\mathrm {Q}_1,\ldots ,\mathrm {Q}_{d-2})$
and use
![]() $\mathrm {V}_{{\textbf {Q}}}(\cdot , \cdot )$
as a shorthand for
$\mathrm {V}_{{\textbf {Q}}}(\cdot , \cdot )$
as a shorthand for
![]() $\mathrm {V}(\cdot , \cdot , \mathrm {Q}_1, \ldots , \mathrm {Q}_{d-2})$
.
$\mathrm {V}(\cdot , \cdot , \mathrm {Q}_1, \ldots , \mathrm {Q}_{d-2})$
.
Theorem 2.2 (Alexandrov–Fenchel inequality; see, e.g., [Reference Burago and ZalgallerBuZ88, Section 20])
The following technical result generalizes Theorem 2.2 to inequalities involving differences in (AF) (see, e.g., [Reference SchneiderSch14, Section 7.4]).
Theorem 2.3 (see, e.g., [Reference SchneiderSch14, Lemma 7.4.1])
We have
 $$ \begin{align} \nonumber & \big(\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{C})^2 - \mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{A}) \hskip.06cm \mathrm{V}_{{\mathbf{ Q}}}(\mathrm{C},\mathrm{C}) \big) \hskip.06cm \big( \mathrm{V}_{{\mathbf{Q}}}(\mathrm{B},\mathrm{C})^2 - \mathrm{V}_{{\mathbf{Q}}}(\mathrm{B},\mathrm{B}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C},\mathrm{C}) \big) \\ & \hskip1.cm \geq \ \big(\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{C}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{B},\mathrm{C}) \ - \ \mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{B}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C},\mathrm{C}) \big)^2. \end{align} $$
$$ \begin{align} \nonumber & \big(\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{C})^2 - \mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{A}) \hskip.06cm \mathrm{V}_{{\mathbf{ Q}}}(\mathrm{C},\mathrm{C}) \big) \hskip.06cm \big( \mathrm{V}_{{\mathbf{Q}}}(\mathrm{B},\mathrm{C})^2 - \mathrm{V}_{{\mathbf{Q}}}(\mathrm{B},\mathrm{B}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C},\mathrm{C}) \big) \\ & \hskip1.cm \geq \ \big(\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{C}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{B},\mathrm{C}) \ - \ \mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{B}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C},\mathrm{C}) \big)^2. \end{align} $$
2.2 Favard’s inequality for the cross-ratio
Toward proving the Main Theorem 1.2, we are most interested in bounds on the cross-ratio
 $$ \begin{align*}{\Upsilon}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{B},\mathrm{C}) \ := \ \frac{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{C}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{B}, \mathrm{C}) }{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{B}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C}, \mathrm{C}) }\,. \end{align*} $$
$$ \begin{align*}{\Upsilon}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{B},\mathrm{C}) \ := \ \frac{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{C}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{B}, \mathrm{C}) }{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{B}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C}, \mathrm{C}) }\,. \end{align*} $$
We start with the following well-known result, which goes back to Favard (see Section 8.2).
Theorem 2.4 (Favard’s inequality; see, e.g., [Reference Brazitikos, Giannopoulos and LiakopoulosBGL18, Lemma 5.1])
Suppose we have
Then,
 $$ \begin{align} \frac{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{C}) \, \mathrm{V}_{{\mathbf{Q}}}(\mathrm{B}, \mathrm{C})}{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{B}) \, \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C}, \mathrm{C})} \ \geq \ \frac{1}{2}\hskip.06cm. \end{align} $$
$$ \begin{align} \frac{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{C}) \, \mathrm{V}_{{\mathbf{Q}}}(\mathrm{B}, \mathrm{C})}{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{B}) \, \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C}, \mathrm{C})} \ \geq \ \frac{1}{2}\hskip.06cm. \end{align} $$
In the next section, we use order polytopes to write the cross-product ratio in (CPC) into the cross-ratio
![]() $\Upsilon $
. Then Favard’s inequality (2.3)
$\Upsilon $
. Then Favard’s inequality (2.3)
![]() $\Upsilon \ge \frac 12$
easily gives the constant
$\Upsilon \ge \frac 12$
easily gives the constant
![]() $\frac 12$
in the inequalities in the Main Theorem 1.2 (see Theorem 3.1). To move beyond
$\frac 12$
in the inequalities in the Main Theorem 1.2 (see Theorem 3.1). To move beyond
![]() $\frac 12$
, we need to strengthen (2.3) (see below).
$\frac 12$
, we need to strengthen (2.3) (see below).
Remark 2.5 From geometric point of view, the constant
![]() $\frac 12$
in the inequality (2.3) is sharp. For example, take
$\frac 12$
in the inequality (2.3) is sharp. For example, take
![]() $\mathrm {A}$
and
$\mathrm {A}$
and
![]() $\mathrm {B}$
non-collinear line segments, and
$\mathrm {B}$
non-collinear line segments, and
![]() $\mathrm {C}=\mathrm {A}+\mathrm {B}$
(see, e.g., [Reference Artstein-Avidan, Florentin and OstroverAFO14, Proposition 5.1] and [Reference Soprunov and ZvavitchSZ16, Theorem 6.1]). However, for various families of convex bodies, it is possible to improve the constant perhaps, although not to 1 as one would wish. For example, when
$\mathrm {C}=\mathrm {A}+\mathrm {B}$
(see, e.g., [Reference Artstein-Avidan, Florentin and OstroverAFO14, Proposition 5.1] and [Reference Soprunov and ZvavitchSZ16, Theorem 6.1]). However, for various families of convex bodies, it is possible to improve the constant perhaps, although not to 1 as one would wish. For example, when
![]() $\mathrm {C}$
is a unit ball in
$\mathrm {C}$
is a unit ball in
![]() $\mathbb R^2$
, the constant can be improved to
$\mathbb R^2$
, the constant can be improved to
![]() $\frac {2}{\pi }$
[Reference Artstein-Avidan, Florentin and OstroverAFO14, Proposition 5.3].
$\frac {2}{\pi }$
[Reference Artstein-Avidan, Florentin and OstroverAFO14, Proposition 5.3].
2.3 Better cross-ratio inequalities
The following two results follow from (2.2) by elementary arguments. They are variations on inequalities that are already known in the literature. We include simple proofs for completeness.
Proposition 2.6 Suppose that
![]() $\mathrm {V}_{{\mathbf {Q}}}(\mathrm {A}, \mathrm {B}) \hskip .06cm \mathrm {V}_{{\mathbf {Q}}}(\mathrm {C}, \mathrm {C})>0$
. Then,
$\mathrm {V}_{{\mathbf {Q}}}(\mathrm {A}, \mathrm {B}) \hskip .06cm \mathrm {V}_{{\mathbf {Q}}}(\mathrm {C}, \mathrm {C})>0$
. Then,
 $$ \begin{align} \frac{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{C}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{B}, \mathrm{C})}{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{B}) \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C}, \mathrm{C})} \ \geq \ \frac{1}{2} \bigg(1 + \frac{\sqrt{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{A}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{B}, \mathrm{B})}}{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{B})} \bigg). \end{align} $$
$$ \begin{align} \frac{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{C}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{B}, \mathrm{C})}{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{B}) \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C}, \mathrm{C})} \ \geq \ \frac{1}{2} \bigg(1 + \frac{\sqrt{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{A}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{B}, \mathrm{B})}}{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{B})} \bigg). \end{align} $$
Proof Let
![]() $\alpha _1,\alpha _2,\beta _1,\beta _2$
be nonnegative real numbers given by
$\alpha _1,\alpha _2,\beta _1,\beta _2$
be nonnegative real numbers given by
 $$\begin{align*}\begin{aligned} \alpha_1 \, &:= \, \frac{{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{C})}}{\sqrt{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{B}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C}, \mathrm{C})}}\, , \qquad && \alpha_2 \, := \, \frac{{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{B}, \mathrm{C})}}{\sqrt{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{B}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C}, \mathrm{C})}}\, , \\ \beta_1 \, &:= \, \frac{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{A})}{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{B})}\,, \qquad && \beta_2 \, := \, \frac{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{B},\mathrm{B})}{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{B})}\,. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \alpha_1 \, &:= \, \frac{{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{C})}}{\sqrt{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{B}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C}, \mathrm{C})}}\, , \qquad && \alpha_2 \, := \, \frac{{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{B}, \mathrm{C})}}{\sqrt{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{B}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C}, \mathrm{C})}}\, , \\ \beta_1 \, &:= \, \frac{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{A})}{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{B})}\,, \qquad && \beta_2 \, := \, \frac{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{B},\mathrm{B})}{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{B})}\,. \end{aligned} \end{align*}$$
Note that
![]() $\beta _1 \beta _2 \leq 1$
by (AF). By perturbing the convex bodies again if necessary, we can without loss of generality assume that
$\beta _1 \beta _2 \leq 1$
by (AF). By perturbing the convex bodies again if necessary, we can without loss of generality assume that
![]() $\beta _1 \beta _2 < 1$
.
$\beta _1 \beta _2 < 1$
.
In this notation, we can rewrite (2.2) as
Rearranging the terms, this gives
By applying the AM–GM inequality to the terms
![]() $\big (\alpha _1^2 \beta _2 + \alpha _2^2 \beta _1 \big )$
, we get
$\big (\alpha _1^2 \beta _2 + \alpha _2^2 \beta _1 \big )$
, we get
Rearranging the terms, this gives
Since
![]() $\beta _1\beta _2< 1$
, we can divide both sides of the inequality above by
$\beta _1\beta _2< 1$
, we can divide both sides of the inequality above by
![]() $\big (1 \hskip .06cm - \hskip .06cm \sqrt {\beta _1\beta _2} \big )$
and get
$\big (1 \hskip .06cm - \hskip .06cm \sqrt {\beta _1\beta _2} \big )$
and get
This gives the desired (2.4).
We now present a variant of Proposition 2.6 in a degenerate case.
Proposition 2.7 Suppose that
![]() $\mathrm {V}_{{\mathbf {Q}}}(\mathrm {A}, \mathrm {B}) \mathrm {V}_{{\mathbf {Q}}}(\mathrm {C}, \mathrm {C})>0$
and
$\mathrm {V}_{{\mathbf {Q}}}(\mathrm {A}, \mathrm {B}) \mathrm {V}_{{\mathbf {Q}}}(\mathrm {C}, \mathrm {C})>0$
and
![]() $\mathrm {V}_{{\mathbf {Q}}}(\mathrm {B},\mathrm {B})=0$
. Then,
$\mathrm {V}_{{\mathbf {Q}}}(\mathrm {B},\mathrm {B})=0$
. Then,
 $$ \begin{align} \frac{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{C}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{B}, \mathrm{C})}{\mathrm{V}_{{\mathbf{ Q}}}(\mathrm{A}, \mathrm{B}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C}, \mathrm{C})} \ \geq \ \bigg(1+ \sqrt{1-\frac{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{A}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C}, \mathrm{C})}{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{C})^2}} \bigg)^{-1}. \end{align} $$
$$ \begin{align} \frac{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{C}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{B}, \mathrm{C})}{\mathrm{V}_{{\mathbf{ Q}}}(\mathrm{A}, \mathrm{B}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C}, \mathrm{C})} \ \geq \ \bigg(1+ \sqrt{1-\frac{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{A}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C}, \mathrm{C})}{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{C})^2}} \bigg)^{-1}. \end{align} $$
Proof First, note that (2.2) gives
 $$ \begin{align} \nonumber & \big(\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{C}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{B},\mathrm{C}) \ - \ \mathrm{V}_{{\mathbf{ Q}}}(\mathrm{A},\mathrm{B}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C},\mathrm{C}) \big)^2 \ \\ & \qquad \leq \ \big(\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{C})^2 - \mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{A}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C},\mathrm{C}) \big) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{B},\mathrm{C})^2. \end{align} $$
$$ \begin{align} \nonumber & \big(\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{C}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{B},\mathrm{C}) \ - \ \mathrm{V}_{{\mathbf{ Q}}}(\mathrm{A},\mathrm{B}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C},\mathrm{C}) \big)^2 \ \\ & \qquad \leq \ \big(\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{C})^2 - \mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{A}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C},\mathrm{C}) \big) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{B},\mathrm{C})^2. \end{align} $$
We assume without loss of generality that
In fact, otherwise, since the right side of (2.6) is at most
![]() $1$
, we immediately have (2.6).
$1$
, we immediately have (2.6).
Now note that
![]() $ \mathrm {V}_{{\mathbf {Q}}}(\mathrm {A},\mathrm {C}) \hskip .06cm \mathrm {V}_{{\mathbf {Q}}}(\mathrm {B},\mathrm {C})> 0$
by (2.3) and by the assumption of the theorem. Taking the square root of (2.7) using (2.8), and then dividing by
$ \mathrm {V}_{{\mathbf {Q}}}(\mathrm {A},\mathrm {C}) \hskip .06cm \mathrm {V}_{{\mathbf {Q}}}(\mathrm {B},\mathrm {C})> 0$
by (2.3) and by the assumption of the theorem. Taking the square root of (2.7) using (2.8), and then dividing by
![]() $ \mathrm {V}_{{\mathbf {Q}}}(\mathrm {A},\mathrm {C}) \hskip .06cm \mathrm {V}_{{\mathbf {Q}}}(\mathrm {B},\mathrm {C})$
, we get
$ \mathrm {V}_{{\mathbf {Q}}}(\mathrm {A},\mathrm {C}) \hskip .06cm \mathrm {V}_{{\mathbf {Q}}}(\mathrm {B},\mathrm {C})$
, we get
 $$\begin{align*}\frac{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{B}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C},\mathrm{C})}{\mathrm{V}_{{\mathbf{ Q}}}(\mathrm{A},\mathrm{C}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{B},\mathrm{C})} \ - \ 1 \ \leq \ \sqrt{1-\frac{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{A}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C}, \mathrm{C})}{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{C})^2}}\,. \end{align*}$$
$$\begin{align*}\frac{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{B}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C},\mathrm{C})}{\mathrm{V}_{{\mathbf{ Q}}}(\mathrm{A},\mathrm{C}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{B},\mathrm{C})} \ - \ 1 \ \leq \ \sqrt{1-\frac{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{A}) \hskip.06cm \mathrm{V}_{{\mathbf{Q}}}(\mathrm{C}, \mathrm{C})}{\mathrm{V}_{{\mathbf{Q}}}(\mathrm{A}, \mathrm{C})^2}}\,. \end{align*}$$
This is equivalent to (2.6).
3 Poset inequalities via mixed volumes
3.1 Definitions and notation
We refer to [Reference TrotterTro95] for some standard posets notation. Let
![]() $P=(X, \prec )$
be a poset with
$P=(X, \prec )$
be a poset with
![]() $|X|=n$
elements. A dual poset is a poset
$|X|=n$
elements. A dual poset is a poset
![]() $P^\ast =(X,\prec ^\ast )$
, where
$P^\ast =(X,\prec ^\ast )$
, where
![]() $x\prec ^\ast y$
if and only if
$x\prec ^\ast y$
if and only if
![]() $y \prec x$
.
$y \prec x$
.
We somewhat change the notation and fix distinct elements
![]() $z_1,z_2,z_3\in X$
which we use throughout the paper. As in the introduction, for
$z_1,z_2,z_3\in X$
which we use throughout the paper. As in the introduction, for
![]() $k,\ell \geq 1$
, let
$k,\ell \geq 1$
, let
and let
![]() $\textrm {F}(k,\ell ) \hskip .03cm := \hskip .03cm \big |\mathcal F(k,\ell )\big |$
. We will write
$\textrm {F}(k,\ell ) \hskip .03cm := \hskip .03cm \big |\mathcal F(k,\ell )\big |$
. We will write
![]() $\textrm {F}_{P,z_1,z_2,z_3}(k,\ell )$
in place of
$\textrm {F}_{P,z_1,z_2,z_3}(k,\ell )$
in place of
![]() $\textrm {F}(k,\ell )$
when there is a potential ambiguity in regard to the underlying poset P and the elements
$\textrm {F}(k,\ell )$
when there is a potential ambiguity in regard to the underlying poset P and the elements
![]() $z_1,z_2, z_3 \in X$
.
$z_1,z_2, z_3 \in X$
.
3.2 Half CPC
We first prove that (CPC) holds up to a factor of
![]() $2$
. Formally, start with the following weak version of the Main Theorem 1.2.
$2$
. Formally, start with the following weak version of the Main Theorem 1.2.
Theorem 3.1 For every
![]() $k,\ell \geq 1$
, we have
$k,\ell \geq 1$
, we have
To prove Theorem 3.1, we will first interpret the quantity
![]() $\textrm {F}(k,\ell )$
as in the language of mixed volumes. Here, we follow Stanley’s approach in [Reference StanleySta81] (see also [Reference Kahn and SaksKS84]).
$\textrm {F}(k,\ell )$
as in the language of mixed volumes. Here, we follow Stanley’s approach in [Reference StanleySta81] (see also [Reference Kahn and SaksKS84]).
Fix a poset
![]() $P=(X,\prec )$
, and let
$P=(X,\prec )$
, and let
![]() $\mathbb {R}^X$
be the space of real vectors
$\mathbb {R}^X$
be the space of real vectors
![]() $\mathbf {v}$
that are indexed by elements
$\mathbf {v}$
that are indexed by elements
![]() $x\in X$
. Throughout this section, the entries of the vector
$x\in X$
. Throughout this section, the entries of the vector
![]() $\mathbf {v}$
that corresponds to
$\mathbf {v}$
that corresponds to
![]() $x \in X$
will be denoted by
$x \in X$
will be denoted by
![]() $\mathbf {v}(x)$
, to maintain legibility when x are substituted with elements
$\mathbf {v}(x)$
, to maintain legibility when x are substituted with elements
![]() $z_i$
. The order polytope
$z_i$
. The order polytope
![]() $\mathrm {K}:=\mathrm {K}(P) \subset \mathbb {R}^X$
is defined as follows:
$\mathrm {K}:=\mathrm {K}(P) \subset \mathbb {R}^X$
is defined as follows:
Let
![]() $\mathrm {K}_1$
,
$\mathrm {K}_1$
,
![]() $\mathrm {K}_2$
,
$\mathrm {K}_2$
,
![]() $\mathrm {K}_3 \subseteq \mathrm {K}$
be the slices of the order polytope defined as follows:
$\mathrm {K}_3 \subseteq \mathrm {K}$
be the slices of the order polytope defined as follows:
 $$ \begin{align} \nonumber \mathrm{K}_1 \ &:= \ \{\hskip.06cm \mathbf{v} \in \mathrm{K} \, : \, \mathbf{v}(z_2) - \mathbf{v}(z_1) \hskip.06cm = \hskip.06cm 1, \ \mathbf{v}(z_3) - \mathbf{v}(z_2) \hskip.06cm = \hskip.06cm 0 \hskip.06cm \}\hskip.03cm,\\ \mathrm{K}_2 \ &:= \ \{\hskip.06cm \mathbf{v} \in \mathrm{K} \, : \, \mathbf{v}(z_2) - \mathbf{v}(z_1) \hskip.06cm = \hskip.06cm 0, \ \mathbf{v}(z_3) - \mathbf{v}(z_2) \hskip.06cm = \hskip.06cm 1 \hskip.06cm \}\hskip.03cm,\\ \nonumber \mathrm{K}_3 \ &:= \ \{\hskip.06cm \mathbf{v} \in \mathrm{K} \, : \, \mathbf{v}(z_2) - \mathbf{v}(z_1) \hskip.06cm = \hskip.06cm \mathbf{v}(z_3) - \mathbf{v}(z_2) \hskip.06cm = \hskip.06cm 0 \hskip.06cm \}\hskip.03cm. \end{align} $$
$$ \begin{align} \nonumber \mathrm{K}_1 \ &:= \ \{\hskip.06cm \mathbf{v} \in \mathrm{K} \, : \, \mathbf{v}(z_2) - \mathbf{v}(z_1) \hskip.06cm = \hskip.06cm 1, \ \mathbf{v}(z_3) - \mathbf{v}(z_2) \hskip.06cm = \hskip.06cm 0 \hskip.06cm \}\hskip.03cm,\\ \mathrm{K}_2 \ &:= \ \{\hskip.06cm \mathbf{v} \in \mathrm{K} \, : \, \mathbf{v}(z_2) - \mathbf{v}(z_1) \hskip.06cm = \hskip.06cm 0, \ \mathbf{v}(z_3) - \mathbf{v}(z_2) \hskip.06cm = \hskip.06cm 1 \hskip.06cm \}\hskip.03cm,\\ \nonumber \mathrm{K}_3 \ &:= \ \{\hskip.06cm \mathbf{v} \in \mathrm{K} \, : \, \mathbf{v}(z_2) - \mathbf{v}(z_1) \hskip.06cm = \hskip.06cm \mathbf{v}(z_3) - \mathbf{v}(z_2) \hskip.06cm = \hskip.06cm 0 \hskip.06cm \}\hskip.03cm. \end{align} $$
Note that all Minkowski sums of these three polytopes have affine dimension
![]() $d=n-2$
.
$d=n-2$
.
Lemma 3.2 Let
![]() $k,\ell \geq 1$
,
$k,\ell \geq 1$
,
![]() $k+\ell \le n$
. We have
$k+\ell \le n$
. We have
 $$ \begin{align} \mathrm{F}(k,\ell) \ = \ (n-2)! \ \mathrm{V}(\underbrace{\mathrm{K}_1,\ldots, \mathrm{K}_1}_{k-1}, \underbrace{\mathrm{K}_2,\ldots,\mathrm{K}_2}_{\ell-1}, \underbrace{\mathrm{K}_3,\ldots, \mathrm{K}_3}_{n-k-\ell}). \end{align} $$
$$ \begin{align} \mathrm{F}(k,\ell) \ = \ (n-2)! \ \mathrm{V}(\underbrace{\mathrm{K}_1,\ldots, \mathrm{K}_1}_{k-1}, \underbrace{\mathrm{K}_2,\ldots,\mathrm{K}_2}_{\ell-1}, \underbrace{\mathrm{K}_3,\ldots, \mathrm{K}_3}_{n-k-\ell}). \end{align} $$
This lemma follows by a variation on the argument in the proof of [Reference StanleySta81, Theorem 3.2] and [Reference Kahn and SaksKS84, Theorem 2.5].
Proof For
![]() $0 < s,t < 1$
,
$0 < s,t < 1$
,
![]() $0 < s+t < 1$
, define
$0 < s+t < 1$
, define
Note that
![]() $\mathrm {K}^{(s,t)} \hskip .06cm = \hskip .06cm s \hskip .03cm \mathrm {K}_1 \hskip .06cm + \hskip .06cm t \hskip .03cm \mathrm {K}_2 \hskip .06cm + \hskip .06cm (1-s-t) \hskip .03cm \mathrm {K}_3$
. Let us now compute the volume of
$\mathrm {K}^{(s,t)} \hskip .06cm = \hskip .06cm s \hskip .03cm \mathrm {K}_1 \hskip .06cm + \hskip .06cm t \hskip .03cm \mathrm {K}_2 \hskip .06cm + \hskip .06cm (1-s-t) \hskip .03cm \mathrm {K}_3$
. Let us now compute the volume of
![]() $\mathrm {K}^{(s,t)}$
.
$\mathrm {K}^{(s,t)}$
.
For every
![]() $L \in \mathcal {E}(P)$
, we denote by
$L \in \mathcal {E}(P)$
, we denote by
![]() $\Delta _{L} \subset \mathrm {K}^{(s,t)}$
the polytope
$\Delta _{L} \subset \mathrm {K}^{(s,t)}$
the polytope
Note that
![]() $\mathrm {K}^{(s,t)}$
is the union of
$\mathrm {K}^{(s,t)}$
is the union of
![]() $\Delta _L$
’s over all linear extensions L such that
$\Delta _L$
’s over all linear extensions L such that
![]() $L(z_1)<L(z_2)<L(z_3)$
, and furthermore all
$L(z_1)<L(z_2)<L(z_3)$
, and furthermore all
![]() $\Delta _L$
’s have pairwise disjoint interiors. Hence, it remains to compute the volume of
$\Delta _L$
’s have pairwise disjoint interiors. Hence, it remains to compute the volume of
![]() $\Delta _L$
’s.
$\Delta _L$
’s.
Let
![]() $L \in \mathcal F(k,\ell )$
for some
$L \in \mathcal F(k,\ell )$
for some
![]() $k,\ell \geq 1$
, let
$k,\ell \geq 1$
, let
![]() $h:=L(z_1)$
, and let
$h:=L(z_1)$
, and let
![]() $x_i$
(
$x_i$
(
![]() $i\in \{1,\ldots ,n\}$
) be the ith smallest element under the total order of L. Note that
$i\in \{1,\ldots ,n\}$
) be the ith smallest element under the total order of L. Note that
![]() $z_1=x_h$
,
$z_1=x_h$
,
![]() $z_2=x_{h+k}$
, and
$z_2=x_{h+k}$
, and
![]() $z_3=x_{h+k+\ell }$
. Then
$z_3=x_{h+k+\ell }$
. Then
![]() $\Delta _L$
consists of
$\Delta _L$
consists of
![]() $\mathbf {v} \in \mathbb {R}^X$
that satisfies these three inequalities:
$\mathbf {v} \in \mathbb {R}^X$
that satisfies these three inequalities:
![]() $0 \leq \mathbf {v}(x_1) \leq \mathbf {v}(x_2) \leq \cdots \leq \mathbf {v}(x_n) \leq 1$
,
$0 \leq \mathbf {v}(x_1) \leq \mathbf {v}(x_2) \leq \cdots \leq \mathbf {v}(x_n) \leq 1$
,
![]() $\mathbf {v}(x_{h+k})=\mathbf {v}(x_{h})+s$
, and
$\mathbf {v}(x_{h+k})=\mathbf {v}(x_{h})+s$
, and
![]() $\mathbf {v}(x_{h+k+\ell })=\mathbf {v}(x_{h})+s+t$
. Denote by
$\mathbf {v}(x_{h+k+\ell })=\mathbf {v}(x_{h})+s+t$
. Denote by
![]() $\Phi : \mathbb {R}^X\to \mathbb {R}^X$
the (volume-preserving) transformation defined as follows:
$\Phi : \mathbb {R}^X\to \mathbb {R}^X$
the (volume-preserving) transformation defined as follows:
![]() $\Phi (\mathbf {v}) = \mathbf {w}$
, where
$\Phi (\mathbf {v}) = \mathbf {w}$
, where
 $$\begin{align*}\begin{aligned} &\mathbf{w}(x_i) \ = \ \mathbf{v}(x_i) \quad && \text{ if } \quad i \hskip.06cm \leq \hskip.06cm h,\\ &\mathbf{w}(x_i) \ = \ \mathbf{v}(x_i)-\mathbf{v}(x_h) \quad && \text{ if } \quad h \hskip.06cm < \hskip.06cm i \hskip.06cm \leq \hskip.06cm h+k,\\ &\mathbf{w}(x_i) \ = \ \mathbf{v}(x_i)-\mathbf{v}(x_h)-s \quad && \text{ if } \quad h+k \hskip.06cm < \hskip.06cm i \hskip.06cm \leq \hskip.06cm h+k+\ell,\\ &\mathbf{w}(x_i) \ = \ \mathbf{v}(x_i)-s-t \quad && \text{ if } \quad h+k+\ell \hskip.06cm < \hskip.06cm i \hskip.06cm \leq \hskip.06cm n\hskip.03cm. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} &\mathbf{w}(x_i) \ = \ \mathbf{v}(x_i) \quad && \text{ if } \quad i \hskip.06cm \leq \hskip.06cm h,\\ &\mathbf{w}(x_i) \ = \ \mathbf{v}(x_i)-\mathbf{v}(x_h) \quad && \text{ if } \quad h \hskip.06cm < \hskip.06cm i \hskip.06cm \leq \hskip.06cm h+k,\\ &\mathbf{w}(x_i) \ = \ \mathbf{v}(x_i)-\mathbf{v}(x_h)-s \quad && \text{ if } \quad h+k \hskip.06cm < \hskip.06cm i \hskip.06cm \leq \hskip.06cm h+k+\ell,\\ &\mathbf{w}(x_i) \ = \ \mathbf{v}(x_i)-s-t \quad && \text{ if } \quad h+k+\ell \hskip.06cm < \hskip.06cm i \hskip.06cm \leq \hskip.06cm n\hskip.03cm. \end{aligned} \end{align*}$$
Then the image
![]() $\Phi (\Delta _L)$
is the set of
$\Phi (\Delta _L)$
is the set of
![]() $\mathbf {w} \in \mathbb {R}^X$
that satisfies
$\mathbf {w} \in \mathbb {R}^X$
that satisfies
 $$\begin{align*}\begin{aligned} &0 \hskip.06cm \leq \hskip.06cm \mathbf{w}(x_1) \hskip.06cm \leq \hskip.06cm \cdots \hskip.06cm \leq \hskip.06cm \mathbf{w}(x_h) \hskip.06cm \leq \hskip.06cm \mathbf{w}(x_{h+k+\ell+1}) \hskip.06cm \leq \hskip.06cm \cdots \hskip.06cm \leq \mathbf{w}({x_n}) \hskip.06cm \leq 1-s-t\hskip.03cm, \\ & 0 \hskip.06cm \leq \hskip.06cm \mathbf{w}(x_{h+1}) \hskip.06cm \leq \hskip.06cm \cdots \hskip.06cm \leq \hskip.06cm \mathbf{w}(x_{h+k}) \hskip.06cm = \hskip.06cm s\hskip.03cm, \quad \text{and}\\ & 0 \hskip.06cm \leq \hskip.06cm \mathbf{w}(x_{h+k+1}) \hskip.06cm \leq \hskip.06cm \cdots \hskip.06cm \leq \hskip.06cm \mathbf{w}(x_{h+k+\ell}) \hskip.06cm = \hskip.06cm t\hskip.03cm. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} &0 \hskip.06cm \leq \hskip.06cm \mathbf{w}(x_1) \hskip.06cm \leq \hskip.06cm \cdots \hskip.06cm \leq \hskip.06cm \mathbf{w}(x_h) \hskip.06cm \leq \hskip.06cm \mathbf{w}(x_{h+k+\ell+1}) \hskip.06cm \leq \hskip.06cm \cdots \hskip.06cm \leq \mathbf{w}({x_n}) \hskip.06cm \leq 1-s-t\hskip.03cm, \\ & 0 \hskip.06cm \leq \hskip.06cm \mathbf{w}(x_{h+1}) \hskip.06cm \leq \hskip.06cm \cdots \hskip.06cm \leq \hskip.06cm \mathbf{w}(x_{h+k}) \hskip.06cm = \hskip.06cm s\hskip.03cm, \quad \text{and}\\ & 0 \hskip.06cm \leq \hskip.06cm \mathbf{w}(x_{h+k+1}) \hskip.06cm \leq \hskip.06cm \cdots \hskip.06cm \leq \hskip.06cm \mathbf{w}(x_{h+k+\ell}) \hskip.06cm = \hskip.06cm t\hskip.03cm. \end{aligned} \end{align*}$$
This set is the direct product of three simplices and has volume
 $$\begin{align*}\rho(s,t) \, := \, \frac{s^{k-1}}{(k-1)!} \hskip.06cm \times \hskip.06cm \frac{t^{\ell-1}}{(\ell-1)!} \hskip.06cm \times \hskip.06cm \frac{(1-s-t)^{n-k-\ell}}{(n-k-\ell)!}\,. \end{align*}$$
$$\begin{align*}\rho(s,t) \, := \, \frac{s^{k-1}}{(k-1)!} \hskip.06cm \times \hskip.06cm \frac{t^{\ell-1}}{(\ell-1)!} \hskip.06cm \times \hskip.06cm \frac{(1-s-t)^{n-k-\ell}}{(n-k-\ell)!}\,. \end{align*}$$
It follows from here that
 $$ \begin{align*} &\mathrm{Vol}_{d}\big(\mathrm{K}^{(s,t)}\big) \ = \ \sum_{k,\ell \geq 1} \, \sum_{L \hskip.03cm\in\hskip.03cm \mathcal F(k,\ell)} \mathrm{Vol}_d(\Delta_L) \ = \ \sum_{k,\ell \geq 1} \hskip.06cm \sum_{L \in \mathcal F(k,\ell)} \hskip.06cm \rho(s,t) \hskip.06cm \\ &\qquad = \ \sum_{k,\ell \geq 1} \binom{n-2}{n-k-\ell, \hskip.06cm k-1, \hskip.06cm \ell-1} \, \frac{\textrm{F}(k,\ell)}{(n-2)!} \,\hskip.06cm s^{k-1} \hskip.06cm t^{\ell-1} \hskip.06cm (1-s-t)^{n-k-\ell}. \end{align*} $$
$$ \begin{align*} &\mathrm{Vol}_{d}\big(\mathrm{K}^{(s,t)}\big) \ = \ \sum_{k,\ell \geq 1} \, \sum_{L \hskip.03cm\in\hskip.03cm \mathcal F(k,\ell)} \mathrm{Vol}_d(\Delta_L) \ = \ \sum_{k,\ell \geq 1} \hskip.06cm \sum_{L \in \mathcal F(k,\ell)} \hskip.06cm \rho(s,t) \hskip.06cm \\ &\qquad = \ \sum_{k,\ell \geq 1} \binom{n-2}{n-k-\ell, \hskip.06cm k-1, \hskip.06cm \ell-1} \, \frac{\textrm{F}(k,\ell)}{(n-2)!} \,\hskip.06cm s^{k-1} \hskip.06cm t^{\ell-1} \hskip.06cm (1-s-t)^{n-k-\ell}. \end{align*} $$
Since the choice of
![]() $s,t$
is arbitrary, equation (3.2) follows from the Minkowski Theorem 2.1.
$s,t$
is arbitrary, equation (3.2) follows from the Minkowski Theorem 2.1.
Proof of Theorem 3.1
Let
![]() $d=n-2$
, and let
$d=n-2$
, and let
![]() $\mathrm {A},\mathrm {B},\mathrm {C}$
,
$\mathrm {A},\mathrm {B},\mathrm {C}$
,
![]() $\mathrm {Q}_1,\ldots , \mathrm {Q}_{d-2} \subset \mathrm {K}$
be given by
$\mathrm {Q}_1,\ldots , \mathrm {Q}_{d-2} \subset \mathrm {K}$
be given by
 $$ \begin{align} \nonumber & \mathrm{A} \, \gets \, \mathrm{K}_1, \quad \mathrm{B} \, \gets \, \mathrm{K}_2, \quad \mathrm{C} \, \gets \, \mathrm{K}_3, \quad \text{and}\\ & \mathrm{Q}_1,\ldots, \mathrm{Q}_{d-2} \, \gets \, \underbrace{\mathrm{K}_1,\ldots, \mathrm{K}_1}_{k-1}, \underbrace{\mathrm{K}_2,\ldots,\mathrm{K}_2}_{\ell-1}, \underbrace{\mathrm{K}_3,\ldots, \mathrm{K}_3}_{n-k-\ell}. \end{align} $$
$$ \begin{align} \nonumber & \mathrm{A} \, \gets \, \mathrm{K}_1, \quad \mathrm{B} \, \gets \, \mathrm{K}_2, \quad \mathrm{C} \, \gets \, \mathrm{K}_3, \quad \text{and}\\ & \mathrm{Q}_1,\ldots, \mathrm{Q}_{d-2} \, \gets \, \underbrace{\mathrm{K}_1,\ldots, \mathrm{K}_1}_{k-1}, \underbrace{\mathrm{K}_2,\ldots,\mathrm{K}_2}_{\ell-1}, \underbrace{\mathrm{K}_3,\ldots, \mathrm{K}_3}_{n-k-\ell}. \end{align} $$
The theorem now follows by applying Lemma 3.2 into Theorem 2.4.
3.3 Applications to cross-products
We now quickly derive the key applications of mixed volume cross-ratio inequalities for the cross-product inequalities.
Proposition 3.3 Suppose that
![]() $\textrm {F}(k,\ell )\hskip .06cm \textrm {F}(k+1,\ell +1)>0$
. Then,
$\textrm {F}(k,\ell )\hskip .06cm \textrm {F}(k+1,\ell +1)>0$
. Then,
 $$ \begin{align*} \frac{ \mathrm{F}(k+1,\ell) \hskip.06cm \mathrm{F}(k,\ell+1) }{\mathrm{F}(k,\ell) \hskip.06cm \mathrm{F}(k+1,\ell+1)} \ \geq \ \frac{1}{2} \ + \ \frac{\sqrt{\mathrm{F}(k,\ell+2)\hskip.06cm \mathrm{F}(k+2,\ell)} }{2 \hskip.06cm \mathrm{F}(k+1,\ell+1)}\,. \end{align*} $$
$$ \begin{align*} \frac{ \mathrm{F}(k+1,\ell) \hskip.06cm \mathrm{F}(k,\ell+1) }{\mathrm{F}(k,\ell) \hskip.06cm \mathrm{F}(k+1,\ell+1)} \ \geq \ \frac{1}{2} \ + \ \frac{\sqrt{\mathrm{F}(k,\ell+2)\hskip.06cm \mathrm{F}(k+2,\ell)} }{2 \hskip.06cm \mathrm{F}(k+1,\ell+1)}\,. \end{align*} $$
Proof Let
![]() $d=n-2$
, and let
$d=n-2$
, and let
![]() $\mathrm {A},\mathrm {B},\mathrm {C}$
,
$\mathrm {A},\mathrm {B},\mathrm {C}$
,
![]() $\mathrm {Q}_1,\ldots , \mathrm {Q}_{d-2} \subset \mathrm {K}$
be given by (3.3). The conclusion of the proposition now follows from Lemma 3.2 and Proposition 2.6.
$\mathrm {Q}_1,\ldots , \mathrm {Q}_{d-2} \subset \mathrm {K}$
be given by (3.3). The conclusion of the proposition now follows from Lemma 3.2 and Proposition 2.6.
Proposition 3.4 Suppose that
![]() $\textrm {F}(k,\ell )\hskip .06cm \textrm {F}(k+1,\ell +1)>0$
and
$\textrm {F}(k,\ell )\hskip .06cm \textrm {F}(k+1,\ell +1)>0$
and
![]() $\textrm {F}(k,\ell +2)=0$
. Then,
$\textrm {F}(k,\ell +2)=0$
. Then,
 $$ \begin{align*} \frac{ \mathrm{F}(k+1,\ell)\mathrm{F}(k,\ell+1) }{\mathrm{F}(k+1,\ell+1)\mathrm{F}(k,\ell)} \ \geq \ \bigg(1 + \sqrt{ 1 - \frac{ \mathrm{F}(k,\ell) \mathrm{F}(k+2,\ell)}{\mathrm{F}(k+1,\ell)^2} } \hskip.06cm \bigg)^{-1}. \end{align*} $$
$$ \begin{align*} \frac{ \mathrm{F}(k+1,\ell)\mathrm{F}(k,\ell+1) }{\mathrm{F}(k+1,\ell+1)\mathrm{F}(k,\ell)} \ \geq \ \bigg(1 + \sqrt{ 1 - \frac{ \mathrm{F}(k,\ell) \mathrm{F}(k+2,\ell)}{\mathrm{F}(k+1,\ell)^2} } \hskip.06cm \bigg)^{-1}. \end{align*} $$
3.4 More half-CPC inequalities
We start with the following half-versions of (CPC1) and (CPC2). The proofs follow the proof of Theorem 3.1 given above.
Lemma 3.5 For every
![]() $k,\ell \geq 1$
, we have
$k,\ell \geq 1$
, we have
Proof We again let
![]() $d=n-2$
and let
$d=n-2$
and let
![]() $\mathrm {Q}_1,\ldots , \mathrm {Q}_{d-2} \subset \mathrm {K}$
be given by (3.3). Then (half-CPC1) follows by applying Lemma 3.2 into Theorem 2.4, with the choice
$\mathrm {Q}_1,\ldots , \mathrm {Q}_{d-2} \subset \mathrm {K}$
be given by (3.3). Then (half-CPC1) follows by applying Lemma 3.2 into Theorem 2.4, with the choice
Similarly, (half-CPC2) follows from the choice
This completes the proof.
Note that (CPC1) is a dual inequality to (CPC2) in the following sense. Let
![]() $P^\ast :=(X,\prec ^\ast )$
be the dual poset of P, i.e.,
$P^\ast :=(X,\prec ^\ast )$
be the dual poset of P, i.e.,
![]() $x\prec ^\ast y$
if and only if
$x\prec ^\ast y$
if and only if
![]() $x\succ y$
. Let
$x\succ y$
. Let
![]() $z_1^\ast :=z_3$
,
$z_1^\ast :=z_3$
,
![]() $z_2^\ast :=z_2$
, and
$z_2^\ast :=z_2$
, and
![]() $z_3^\ast :=z_1$
. Then
$z_3^\ast :=z_1$
. Then
![]() $\textrm {F}_{P,z_1,z_2,z_3}(k,\ell ) = \textrm {F}_{P^\ast , z_1^\ast ,z_2^\ast ,z_3^\ast }(\ell ,k)$
by the maps that send linear extensions of P to linear extensions of
$\textrm {F}_{P,z_1,z_2,z_3}(k,\ell ) = \textrm {F}_{P^\ast , z_1^\ast ,z_2^\ast ,z_3^\ast }(\ell ,k)$
by the maps that send linear extensions of P to linear extensions of
![]() $P^\ast $
by reversing the total order.
$P^\ast $
by reversing the total order.
On the other hand, one can think of (CPC1) and (CPC2) as negative variants of (CPC), in the following sense. Let
![]() $z_1':=z_2$
,
$z_1':=z_2$
,
![]() $z_2':=z_1$
, and
$z_2':=z_1$
, and
![]() $z_3':=z_3$
, and we write
$z_3':=z_3$
, and we write
![]() $\textrm {F}= \textrm {F}_{P,z_1,z_2,z_3}$
and
$\textrm {F}= \textrm {F}_{P,z_1,z_2,z_3}$
and
![]() $\textrm {F}'= \textrm {F}_{P,z_1',z_2',z_3'}$
. Then, for every integer
$\textrm {F}'= \textrm {F}_{P,z_1',z_2',z_3'}$
. Then, for every integer
![]() $k,\ell $
,
$k,\ell $
,
 $$ \begin{align*} \textrm{F}(k,\ell) \ &= \ \big|\{L \in \mathcal{E}(P) \, : \, L(z_2)-L(z_1)=k, \hskip.06cm L(z_3)-L(z_2)=\ell \}\big|\\ \ &= \ \big|\{L \in \mathcal{E}(P) \, : \, L(z_1)-L(z_2)=-k, \hskip.06cm L(z_3)-L(z_1)=\ell+k \}\big|\\ \ &= \ \textrm{F}'(-k, \ell+ k). \end{align*} $$
$$ \begin{align*} \textrm{F}(k,\ell) \ &= \ \big|\{L \in \mathcal{E}(P) \, : \, L(z_2)-L(z_1)=k, \hskip.06cm L(z_3)-L(z_2)=\ell \}\big|\\ \ &= \ \big|\{L \in \mathcal{E}(P) \, : \, L(z_1)-L(z_2)=-k, \hskip.06cm L(z_3)-L(z_1)=\ell+k \}\big|\\ \ &= \ \textrm{F}'(-k, \ell+ k). \end{align*} $$
Let
![]() $k':=-k-1$
and
$k':=-k-1$
and
![]() $\ell ':=\ell +k$
. Under this change of variable, (CPC) then becomes
$\ell ':=\ell +k$
. Under this change of variable, (CPC) then becomes
which coincides with (CPC2) in this case.
Note, however, that (CPC) does not imply (CPC1) and vice versa, since
![]() $k'$
are necessarily negative under this transformation. In fact, as mentioned in the introduction, we will present counterexamples to (CPC1) in Section 7.2.
$k'$
are necessarily negative under this transformation. In fact, as mentioned in the introduction, we will present counterexamples to (CPC1) in Section 7.2.
3.5 Variations on the theme
The following three inequalities are variations on (CPC).
Lemma 3.6 For every
![]() $k,\ell \geq 1$
, we have
$k,\ell \geq 1$
, we have
Proof Let
![]() $d=n-2$
, and let
$d=n-2$
, and let
![]() $\mathrm {A},\mathrm {B},\mathrm {C}$
,
$\mathrm {A},\mathrm {B},\mathrm {C}$
,
![]() $\mathrm {Q}_1,\ldots , \mathrm {Q}_{d-2} \subset \mathrm {K}$
be given by (3.3). It follows from the Alexandrov–Fenchel inequality (AF) that
$\mathrm {Q}_1,\ldots , \mathrm {Q}_{d-2} \subset \mathrm {K}$
be given by (3.3). It follows from the Alexandrov–Fenchel inequality (AF) that
 $$ \begin{align*} \mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{B})^2 \ &\geq \ \mathrm{V}(\mathrm{A},\mathrm{A}) \ \mathrm{V}(\mathrm{B},\mathrm{B}),\\ \mathrm{V}_{{\mathbf{Q}}}(\mathrm{B},\mathrm{C})^2 \ &\geq \ \mathrm{V}(\mathrm{B},\mathrm{B}) \ \mathrm{V}(\mathrm{C},\mathrm{C}),\\ \mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{C})^2 \ &\geq \ \mathrm{V}(\mathrm{A},\mathrm{A}) \ \mathrm{V}(\mathrm{C},\mathrm{C}). \end{align*} $$
$$ \begin{align*} \mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{B})^2 \ &\geq \ \mathrm{V}(\mathrm{A},\mathrm{A}) \ \mathrm{V}(\mathrm{B},\mathrm{B}),\\ \mathrm{V}_{{\mathbf{Q}}}(\mathrm{B},\mathrm{C})^2 \ &\geq \ \mathrm{V}(\mathrm{B},\mathrm{B}) \ \mathrm{V}(\mathrm{C},\mathrm{C}),\\ \mathrm{V}_{{\mathbf{Q}}}(\mathrm{A},\mathrm{C})^2 \ &\geq \ \mathrm{V}(\mathrm{A},\mathrm{A}) \ \mathrm{V}(\mathrm{C},\mathrm{C}). \end{align*} $$
By applying Lemma 3.2, we get the desired inequalities.
Remark 3.7 The inequalities (LogC-1), (LogC-2), and (LogC-3) can be viewed as extensions of Stanley’s and Kahn–Saks inequalities (cf. [Reference Chan, Pak and PanovaCPP22, Reference Chan, Pak and PanovaCPP23b]).
Corollary 3.8 Suppose that
![]() $\textrm {F}(k,\ell ) \hskip .06cm \textrm {F}(k+1,\ell +1)>0$
. Then we have
$\textrm {F}(k,\ell ) \hskip .06cm \textrm {F}(k+1,\ell +1)>0$
. Then we have
 $$\begin{align*}\frac{\mathrm{F}(k+1,\ell) \hskip.06cm \mathrm{F}(k,\ell+1)}{\mathrm{F}(k,\ell) \hskip.06cm \mathrm{F}(k+1,\ell+1)} \ \geq \ \frac{\mathrm{F}(k+2,\ell) \hskip.06cm \mathrm{F}(k,\ell+2)}{\mathrm{F}(k+1,\ell+1)^2} \,. \end{align*}$$
$$\begin{align*}\frac{\mathrm{F}(k+1,\ell) \hskip.06cm \mathrm{F}(k,\ell+1)}{\mathrm{F}(k,\ell) \hskip.06cm \mathrm{F}(k+1,\ell+1)} \ \geq \ \frac{\mathrm{F}(k+2,\ell) \hskip.06cm \mathrm{F}(k,\ell+2)}{\mathrm{F}(k+1,\ell+1)^2} \,. \end{align*}$$
In particular, if (LogC-1) is an equality, then the inequality (CPC) holds.
Proof Taking the product of (LogC-1), (LogC-2), and (LogC-3), we have
By the assumptions, this implies the result.Footnote 3
Proof of Theorem 1.7
First, assume that both (CPC1) and (CPC2) are false:
 $$ \begin{align*} & \textrm{F}(k+2,\ell) \hskip.06cm \textrm{F}(k,\ell+1) > \textrm{F}(k+1,\ell) \hskip.06cm \textrm{F}(k+1,\ell+1) \quad \text{ and } \\ & \textrm{F}(k,\ell+2) \hskip.06cm \textrm{F}(k+1,\ell) \ > \ \textrm{F}(k,\ell+1) \hskip.06cm \textrm{F}(k+1,\ell+1). \end{align*} $$
$$ \begin{align*} & \textrm{F}(k+2,\ell) \hskip.06cm \textrm{F}(k,\ell+1) > \textrm{F}(k+1,\ell) \hskip.06cm \textrm{F}(k+1,\ell+1) \quad \text{ and } \\ & \textrm{F}(k,\ell+2) \hskip.06cm \textrm{F}(k+1,\ell) \ > \ \textrm{F}(k,\ell+1) \hskip.06cm \textrm{F}(k+1,\ell+1). \end{align*} $$
Taking the product of both inequalities, we then get
which contradicts (LogC-1). The proofs for the other cases are analogous.
4 Vanishing of poset inequalities
4.1 Poset parameters
For an element
![]() $x \in X$
, let
$x \in X$
, let
![]() $B(x) := \big \{y \in X \hskip .06cm : \hskip .06cm y \preccurlyeq x \big \}$
denote the lower-order ideal generated by x, and let
$B(x) := \big \{y \in X \hskip .06cm : \hskip .06cm y \preccurlyeq x \big \}$
denote the lower-order ideal generated by x, and let
![]() $b(x):=|B(x)|$
. Similarly, let
$b(x):=|B(x)|$
. Similarly, let
![]() $B^\ast (x) := \big \{y \in X \hskip .06cm : \hskip .06cm y \succcurlyeq x \big \}$
denote the upper-order ideal generated by x, and let
$B^\ast (x) := \big \{y \in X \hskip .06cm : \hskip .06cm y \succcurlyeq x \big \}$
denote the upper-order ideal generated by x, and let
![]() $b^\ast (x):=|B^\ast (x)|$
.
$b^\ast (x):=|B^\ast (x)|$
.
By analogy, let
![]() $B(x,y) = \{ z\in X \hskip .06cm : \hskip .06cm x \preccurlyeq z \preccurlyeq y\}$
be the interval between x and y, and let
$B(x,y) = \{ z\in X \hskip .06cm : \hskip .06cm x \preccurlyeq z \preccurlyeq y\}$
be the interval between x and y, and let
![]() $b(x,y) = |B(x,y)|$
. Without loss of generality, we can always assume that
$b(x,y) = |B(x,y)|$
. Without loss of generality, we can always assume that
![]() $z_1\prec z_2 \prec z_3$
, since otherwise these relations can be added to the poset. We then have
$z_1\prec z_2 \prec z_3$
, since otherwise these relations can be added to the poset. We then have
![]() $b(z_1,z_2)$
,
$b(z_1,z_2)$
,
![]() $b(z_2,z_3) \geq 2$
.
$b(z_2,z_3) \geq 2$
.
Let
![]() $x,y\in X$
be two incomparable elements in P, and write
$x,y\in X$
be two incomparable elements in P, and write
![]() $y\hskip .03cm\|\hskip .03cm{}x$
. Define
$y\hskip .03cm\|\hskip .03cm{}x$
. Define
Similarly, define
Finally, let
and we define
![]() $t(x):=1, \hskip .06cm t^*(x):=1$
if every element
$t(x):=1, \hskip .06cm t^*(x):=1$
if every element
![]() $y \in X$
is comparable to x. Clearly,
$y \in X$
is comparable to x. Clearly,
![]() $t(x) \leq b(x)$
and
$t(x) \leq b(x)$
and
![]() $t^*(x) \leq b^*(x)$
, by definition.
$t^*(x) \leq b^*(x)$
, by definition.
In this notation, recall that a poset
![]() $P=(X,\prec )$
is
t-thin with respect to A
, if for every
$P=(X,\prec )$
is
t-thin with respect to A
, if for every
![]() $u \in X\smallsetminus A$
we have
$u \in X\smallsetminus A$
we have
![]() $n-b(u)-b^*(u)\le t-1$
. Similarly, recall that a poset
$n-b(u)-b^*(u)\le t-1$
. Similarly, recall that a poset
![]() $P=(X,\prec )$
is
t-flat with respect to A
, if for every
$P=(X,\prec )$
is
t-flat with respect to A
, if for every
![]() $u \in A$
we have
$u \in A$
we have
![]() $b(u)+b^*(u)\le t+1$
. Note that
$b(u)+b^*(u)\le t+1$
. Note that
![]() $t(u),t^*(u) \leq t$
in either case.
$t(u),t^*(u) \leq t$
in either case.
4.2 Vanishing conditions
Recall the following conditions for existence of restricted linear extensions.
Theorem 4.1 ([Reference Chan, Pak and PanovaCPP23a, Theorem 1.12])
Let
![]() $P=(X,\prec )$
be a poset with
$P=(X,\prec )$
be a poset with
![]() $|X|=n$
elements, and let
$|X|=n$
elements, and let
![]() $z_1,\ldots ,z_r\in X$
be distinct elements such that
$z_1,\ldots ,z_r\in X$
be distinct elements such that
![]() $z_1 \prec z_2 \prec \cdots \prec z_r$
. Fix integers
$z_1 \prec z_2 \prec \cdots \prec z_r$
. Fix integers
![]() $1\leq a_1<a_2<\cdots <a_r \leq n$
. Then there exists a linear extension
$1\leq a_1<a_2<\cdots <a_r \leq n$
. Then there exists a linear extension
![]() $L\in \mathcal {E}(P)$
with
$L\in \mathcal {E}(P)$
with
![]() $L(z_i)=a_i$
for all
$L(z_i)=a_i$
for all
![]() $1\le i \le r$
if and only if
$1\le i \le r$
if and only if
 $$ \begin{align} \big\{\, \nonumber & b(z_i)\hskip.06cm \le \hskip.06cm a_i \hskip.06cm, \ \, b^*(z_i)\le n-a_i+1 \ \ \text{for all} \ \ 1\hskip.06cm\le \hskip.06cm i \hskip.06cm \le \hskip.06cm r\hskip.03cm, \ \, \text{and} \\ & a_j \hskip.06cm - \hskip.06cm a_i \, \geq \, b(z_i,z_j) -1 \ \ \text{for all} \ \ 1\hskip.06cm\le \hskip.06cm i \hskip.06cm < \hskip.06cm j \hskip.06cm \le \hskip.06cm r\hskip.03cm. \end{align} $$
$$ \begin{align} \big\{\, \nonumber & b(z_i)\hskip.06cm \le \hskip.06cm a_i \hskip.06cm, \ \, b^*(z_i)\le n-a_i+1 \ \ \text{for all} \ \ 1\hskip.06cm\le \hskip.06cm i \hskip.06cm \le \hskip.06cm r\hskip.03cm, \ \, \text{and} \\ & a_j \hskip.06cm - \hskip.06cm a_i \, \geq \, b(z_i,z_j) -1 \ \ \text{for all} \ \ 1\hskip.06cm\le \hskip.06cm i \hskip.06cm < \hskip.06cm j \hskip.06cm \le \hskip.06cm r\hskip.03cm. \end{align} $$
We apply this result to determine the vanishing conditions for
![]() $\textrm {F}(k,\ell )$
.
$\textrm {F}(k,\ell )$
.
Theorem 4.2 Let
![]() $P=(X,\prec )$
be a poset with
$P=(X,\prec )$
be a poset with
![]() $|X|=n$
elements, and let
$|X|=n$
elements, and let
![]() $z_1\prec z_2\prec z_3$
be distinct elements in X. Then
$z_1\prec z_2\prec z_3$
be distinct elements in X. Then
![]() $\textrm {F}(k,\ell )>0$
if and only if
$\textrm {F}(k,\ell )>0$
if and only if
 $$ \begin{align*}\begin{array}{lcl} b(z_1,z_2)-1\ \leq & k &\leq \ n+1 - b(z_1) - b^*(z_2), \\ b(z_2,z_3)-1 \ \leq & \ell &\leq \ n+1 - b^*(z_3) - b(z_2), \\ b(z_1,z_3)-1\ \leq & k + \ell &\leq \ n+1 - b^*(z_3)-b(z_1). \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{lcl} b(z_1,z_2)-1\ \leq & k &\leq \ n+1 - b(z_1) - b^*(z_2), \\ b(z_2,z_3)-1 \ \leq & \ell &\leq \ n+1 - b^*(z_3) - b(z_2), \\ b(z_1,z_3)-1\ \leq & k + \ell &\leq \ n+1 - b^*(z_3)-b(z_1). \end{array}\end{align*} $$
Note that conditions in the theorem can be viewed as six linear inequalities for
![]() $(k,\ell )\in \mathbb N^2$
. These inequalities determine a convex polygon in
$(k,\ell )\in \mathbb N^2$
. These inequalities determine a convex polygon in
![]() $\mathbb R^2$
(see below).
$\mathbb R^2$
(see below).
Proof We have that
![]() $\textrm {F}(k,\ell )>0$
if and only if there exists an integer a, such that the conditions of Theorem 4.1 are satisfied for the elements
$\textrm {F}(k,\ell )>0$
if and only if there exists an integer a, such that the conditions of Theorem 4.1 are satisfied for the elements
![]() $z_1 \prec z_2 \prec z_3$
with
$z_1 \prec z_2 \prec z_3$
with
![]() $a_1 =a, a_2=a+k, a_3=a+k+\ell $
. Rewriting the inequalities, we obtain the following conditions:
$a_1 =a, a_2=a+k, a_3=a+k+\ell $
. Rewriting the inequalities, we obtain the following conditions:
 $$ \begin{align*} & b(z_1,z_2) \leq k+1 \hskip.06cm,\quad b(z_2,z_3) \leq \ell+1 \hskip.06cm, \quad b(z_1,z_3) \leq k +\ell+1 \qquad \text{ and }\\ & \max\{b(z_1), b(z_2)-k,b(z_3)-k-\ell\} \leq a \leq n+1- \max\{b^*(z_1), k+b^*(z_2), k+\ell+b^*(z_3)\}. \end{align*} $$
$$ \begin{align*} & b(z_1,z_2) \leq k+1 \hskip.06cm,\quad b(z_2,z_3) \leq \ell+1 \hskip.06cm, \quad b(z_1,z_3) \leq k +\ell+1 \qquad \text{ and }\\ & \max\{b(z_1), b(z_2)-k,b(z_3)-k-\ell\} \leq a \leq n+1- \max\{b^*(z_1), k+b^*(z_2), k+\ell+b^*(z_3)\}. \end{align*} $$
The integer a exists if and only if the last inequalities are consistent, which leads to
 $$ \begin{align*} & b(z_1,z_2)+1 \leq k \hskip.06cm,\quad b(z_2,z_3)+1 \leq \ell \hskip.06cm, \quad b(z_1,z_3)+1 \leq k +\ell \qquad \text{ and }\\ & \max\{b(z_1), b(z_2)-k,b(z_3)-k-\ell\} + \max\{b^*(z_1), k+b^*(z_2), k+\ell+b^*(z_3)\} \leq n+1. \end{align*} $$
$$ \begin{align*} & b(z_1,z_2)+1 \leq k \hskip.06cm,\quad b(z_2,z_3)+1 \leq \ell \hskip.06cm, \quad b(z_1,z_3)+1 \leq k +\ell \qquad \text{ and }\\ & \max\{b(z_1), b(z_2)-k,b(z_3)-k-\ell\} + \max\{b^*(z_1), k+b^*(z_2), k+\ell+b^*(z_3)\} \leq n+1. \end{align*} $$
Noting that
![]() $b(z_i) +b^*(z_i) \leq n+1$
for all i, the second inequality translates to six unconditional linear inequalities for k and
$b(z_i) +b^*(z_i) \leq n+1$
for all i, the second inequality translates to six unconditional linear inequalities for k and
![]() $\ell $
, which can be written as
$\ell $
, which can be written as
 $$ \begin{align*}\begin{array}{lcl} b(z_2)+b^*(z_1) - n-1 \ \leq & k &\leq \ n+1 - b(z_1) - b^*(z_2), \\ b^*(z_2)+b(z_3) -n-1 \ \leq & \ell &\leq \ n+1 - b^*(z_3) - b(z_2), \\ b^*(z_1)+b(z_3) -n-1 \ \leq & k + \ell &\leq \ n+1 - b^*(z_3)-b(z_1).\end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{lcl} b(z_2)+b^*(z_1) - n-1 \ \leq & k &\leq \ n+1 - b(z_1) - b^*(z_2), \\ b^*(z_2)+b(z_3) -n-1 \ \leq & \ell &\leq \ n+1 - b^*(z_3) - b(z_2), \\ b^*(z_1)+b(z_3) -n-1 \ \leq & k + \ell &\leq \ n+1 - b^*(z_3)-b(z_1).\end{array} \end{align*} $$
Finally, since
![]() $|X|=n$
, we also have
$|X|=n$
, we also have
Combining with the previous inequalities, we obtain the desired conditions.
Corollary 4.3 Suppose that
![]() $\textrm {F}(k+1,\ell ) \hskip .06cm \textrm {F}(k,\ell +1)=0$
. Then
$\textrm {F}(k+1,\ell ) \hskip .06cm \textrm {F}(k,\ell +1)=0$
. Then
![]() $\textrm {F}(k,\ell )\hskip .06cm \textrm {F}(k+1, \ell +1)=0$
.
$\textrm {F}(k,\ell )\hskip .06cm \textrm {F}(k+1, \ell +1)=0$
.
Proof Let
![]() $\mathcal S:= \big \{(k,\ell )\in \mathbb N^2 \hskip .06cm : \hskip .06cm \textrm {F}(k,\ell )>0\big \}$
denote the support of
$\mathcal S:= \big \{(k,\ell )\in \mathbb N^2 \hskip .06cm : \hskip .06cm \textrm {F}(k,\ell )>0\big \}$
denote the support of
![]() $\textrm {F}(\cdot ,\cdot )$
. By Theorem 4.2, we have
$\textrm {F}(\cdot ,\cdot )$
. By Theorem 4.2, we have
![]() $\mathcal S$
is a (possibly degenerate) hexagon with sides parallel to the axis and the line
$\mathcal S$
is a (possibly degenerate) hexagon with sides parallel to the axis and the line
![]() $k+\ell =0$
. Observe that if
$k+\ell =0$
. Observe that if
![]() $(k,\ell ), \hskip .03cm (k+1,\ell +1)\in \mathcal S$
, then we also have
$(k,\ell ), \hskip .03cm (k+1,\ell +1)\in \mathcal S$
, then we also have
![]() $(k+1,\ell ), \hskip .03cm (k,\ell +1)\in \mathcal S$
. In other words, if
$(k+1,\ell ), \hskip .03cm (k,\ell +1)\in \mathcal S$
. In other words, if
![]() $\textrm {F}(k,\ell )\hskip .06cm \textrm {F}(k+1,\ell +1)=0$
, then we also have
$\textrm {F}(k,\ell )\hskip .06cm \textrm {F}(k+1,\ell +1)=0$
, then we also have
![]() $\textrm {F}(k+1,\ell ) \hskip .06cm \textrm {F}(k,\ell +1)=0$
, as desired.
$\textrm {F}(k+1,\ell ) \hskip .06cm \textrm {F}(k,\ell +1)=0$
, as desired.
4.3 Cross-product equality in the vanishing case
We are now ready to prove (1.4) in the main theorem.
Lemma 4.4 Let
![]() $P=(X,\prec )$
be a finite poset, and let
$P=(X,\prec )$
be a finite poset, and let
![]() $z_1 \prec z_2 \prec z_3$
be three distinct elements in X. Suppose that
$z_1 \prec z_2 \prec z_3$
be three distinct elements in X. Suppose that
![]() $\textrm {F}(k,\ell +2)=\textrm {F}(k+2,\ell )=0$
and
$\textrm {F}(k,\ell +2)=\textrm {F}(k+2,\ell )=0$
and
![]() $\textrm {F}(k,\ell ) \hskip .06cm \textrm {F}(k+1,\ell +1)> 0$
. Then
$\textrm {F}(k,\ell ) \hskip .06cm \textrm {F}(k+1,\ell +1)> 0$
. Then
Proof As in the proof of Corollary 4.3, let
![]() $\mathcal S:= \big \{(k,\ell )\in \mathbb N^2 \hskip .06cm : \hskip .06cm \textrm {F}(k,\ell )>0\big \}$
denote the support of
$\mathcal S:= \big \{(k,\ell )\in \mathbb N^2 \hskip .06cm : \hskip .06cm \textrm {F}(k,\ell )>0\big \}$
denote the support of
![]() $\textrm {F}(\cdot ,\cdot )$
. By the assumption, we have
$\textrm {F}(\cdot ,\cdot )$
. By the assumption, we have
![]() $(k,\ell +2), \hskip .03cm (k+2,\ell )\not \in \mathcal S$
and
$(k,\ell +2), \hskip .03cm (k+2,\ell )\not \in \mathcal S$
and
![]() $(k,\ell ), (k+1,\ell +1)\in \mathcal S$
. Theorem 4.2 then gives
$(k,\ell ), (k+1,\ell +1)\in \mathcal S$
. Theorem 4.2 then gives
Together these imply
Theorem 4.2 also gives
Substituting
![]() $(\ast )$
into this inequality, we get
$(\ast )$
into this inequality, we get
This simplifies to
![]() $n+1 \leq b(z_2) +b^*(z_2)$
and implies that all elements in X are comparable to
$n+1 \leq b(z_2) +b^*(z_2)$
and implies that all elements in X are comparable to
![]() $z_2$
.
$z_2$
.
Let
![]() $S= B(z_2)-z_2$
and
$S= B(z_2)-z_2$
and
![]() $T =B^*(z_2)-z_2$
be the lower set and upper sets of
$T =B^*(z_2)-z_2$
be the lower set and upper sets of
![]() $z_2$
, respectively. Denote
$z_2$
, respectively. Denote
![]() $s:=|S| = b(z_2)-1$
and
$s:=|S| = b(z_2)-1$
and
![]() $t:=|T|=b^*(z_2)-1$
. Note that
$t:=|T|=b^*(z_2)-1$
. Note that
![]() $X=S \sqcup T \sqcup \{z_2\}$
by the argument above.
$X=S \sqcup T \sqcup \{z_2\}$
by the argument above.
Let
![]() $1\le r \le n$
. Consider a subposet
$1\le r \le n$
. Consider a subposet
![]() $(S,\prec )$
of
$(S,\prec )$
of
![]() $P=(X,\prec )$
and denote by
$P=(X,\prec )$
and denote by
![]() $\textrm {N}_{r}$
the number of linear extensions L of
$\textrm {N}_{r}$
the number of linear extensions L of
![]() $(S,\prec )$
such that
$(S,\prec )$
such that
![]() $L(z_1)=r$
. Similarly, consider a subposet
$L(z_1)=r$
. Similarly, consider a subposet
![]() $(T,\prec )$
of
$(T,\prec )$
of
![]() $P=(X,\prec )$
and denote by
$P=(X,\prec )$
and denote by
![]() $\textrm {N}_{r}'$
the number of linear extensions L of
$\textrm {N}_{r}'$
the number of linear extensions L of
![]() $(S,\prec )$
such that
$(S,\prec )$
such that
![]() $L(z_3)=r$
.
$L(z_3)=r$
.
Since
![]() $z_1 \prec z_2\prec z_3$
, we have
$z_1 \prec z_2\prec z_3$
, we have
![]() $z_1 \in S$
and
$z_1 \in S$
and
![]() $z_3 \in T$
. Therefore, for all
$z_3 \in T$
. Therefore, for all
![]() $p,q\ge 1$
, we have
$p,q\ge 1$
, we have
This implies that
 $$ \begin{align*} & \textrm{F}(k,\ell+1) \hskip.06cm \textrm{F}(k+1,\ell) \ = \ \textrm{N}_{s-k+1} \, \textrm{N}_{\ell+1}' \, \textrm{N}_{s-k} \, \textrm{N}_{\ell}' \\ & \qquad = \ \textrm{N}_{s-k} \, \textrm{N}_{\ell+1}' \, \textrm{N}_{s-k+1} \, \textrm{N}_{\ell}' \ = \ \textrm{F}(k+1,\ell+1) \hskip.06cm \textrm{F}(k,\ell), \end{align*} $$
$$ \begin{align*} & \textrm{F}(k,\ell+1) \hskip.06cm \textrm{F}(k+1,\ell) \ = \ \textrm{N}_{s-k+1} \, \textrm{N}_{\ell+1}' \, \textrm{N}_{s-k} \, \textrm{N}_{\ell}' \\ & \qquad = \ \textrm{N}_{s-k} \, \textrm{N}_{\ell+1}' \, \textrm{N}_{s-k+1} \, \textrm{N}_{\ell}' \ = \ \textrm{F}(k+1,\ell+1) \hskip.06cm \textrm{F}(k,\ell), \end{align*} $$
as desired.
Example 4.5 For
![]() $k, \ell \ge 1$
, let
$k, \ell \ge 1$
, let
![]() $X:=\{x_1,\ldots ,x_{k+\ell -1},z_1,z_2,z_3\}$
. Consider a poset
$X:=\{x_1,\ldots ,x_{k+\ell -1},z_1,z_2,z_3\}$
. Consider a poset
![]() $P=(X,\prec )$
, where
$P=(X,\prec )$
, where
![]() $A:=\{x_1,\ldots ,x_{k+\ell -1},z_2\}$
is an antichain, and
$A:=\{x_1,\ldots ,x_{k+\ell -1},z_2\}$
is an antichain, and
![]() $z_1\prec A \prec z_3$
. Observe that
$z_1\prec A \prec z_3$
. Observe that
 $$ \begin{align*}\textrm{F}(k,\ell)&= \textrm{F}(k+1,\ell+1)=\textrm{F}(k,\ell+2)=\textrm{F}(k+2,\ell)=0,\\\textrm{F}(k,\ell+1) \hskip.06cm &= \hskip.06cm \tbinom{k+\ell-1}{k-1} \quad \text{and} \quad \textrm{F}(k+1,\ell) \hskip.06cm = \hskip.06cm \tbinom{k+\ell-1}{k}\hskip.03cm.\end{align*} $$
$$ \begin{align*}\textrm{F}(k,\ell)&= \textrm{F}(k+1,\ell+1)=\textrm{F}(k,\ell+2)=\textrm{F}(k+2,\ell)=0,\\\textrm{F}(k,\ell+1) \hskip.06cm &= \hskip.06cm \tbinom{k+\ell-1}{k-1} \quad \text{and} \quad \textrm{F}(k+1,\ell) \hskip.06cm = \hskip.06cm \tbinom{k+\ell-1}{k}\hskip.03cm.\end{align*} $$
Then we have
This shows that the nonvanishing assumption
![]() $\textrm {F}(k,\ell ) \hskip .06cm \textrm {F}(k+1,\ell +1)> 0$
in Lemma 4.4 cannot be dropped.
$\textrm {F}(k,\ell ) \hskip .06cm \textrm {F}(k+1,\ell +1)> 0$
in Lemma 4.4 cannot be dropped.
5 Cross-product inequalities in the nonvanishing case
5.1 Algebraic setup
We employ the algebraic framework from [Reference Chan, Pak and PanovaCPP23b, Section 6]. With every linear extension
![]() $L\in \mathcal {E}(P)$
, we associate a word
$L\in \mathcal {E}(P)$
, we associate a word
![]() ${\mathbf{x}}_L \hskip .03cm=\hskip .03cm x_1\ldots x_n\hskip .03cm \in X^\ast $
, such that
${\mathbf{x}}_L \hskip .03cm=\hskip .03cm x_1\ldots x_n\hskip .03cm \in X^\ast $
, such that
![]() $L(x_i) =i$
for all
$L(x_i) =i$
for all
![]() $1\le i \le n$
. In the notation of the previous section, this says that
$1\le i \le n$
. In the notation of the previous section, this says that
![]() $X=\{x_1,\ldots ,x_n\}$
is a natural labeling corresponding to L.
$X=\{x_1,\ldots ,x_n\}$
is a natural labeling corresponding to L.
We can now define the following action of the group
![]() $\textrm {G}_n$
on
$\textrm {G}_n$
on
![]() $\mathcal {E}(P)$
as the right action on the words
$\mathcal {E}(P)$
as the right action on the words
![]() ${\mathbf{x}}_L$
,
${\mathbf{x}}_L$
,
![]() $L\in \mathcal {E}(P)$
. For
$L\in \mathcal {E}(P)$
. For
![]() ${\mathbf{x}}_L \hskip .03cm =\hskip .03cm x_1\ldots \hskip .03cm x_n$
as above, let
${\mathbf{x}}_L \hskip .03cm =\hskip .03cm x_1\ldots \hskip .03cm x_n$
as above, let
 $$ \begin{align} (x_1\ldots \hskip.03cm x_n) \hskip.06cm \tau_i \ := \ \begin{cases} \ x_1 \ldots \hskip.03cm x_n, & \ \text{if}\quad x_i \prec x_{i+1}\hskip.03cm,\\ \ x_1\dots x_{i+1} \hskip.03cm x_i \dots x_n\hskip.03cm, & \ \text{if}\quad x_i \parallel x_{i+1}\hskip.03cm. \end{cases} \end{align} $$
$$ \begin{align} (x_1\ldots \hskip.03cm x_n) \hskip.06cm \tau_i \ := \ \begin{cases} \ x_1 \ldots \hskip.03cm x_n, & \ \text{if}\quad x_i \prec x_{i+1}\hskip.03cm,\\ \ x_1\dots x_{i+1} \hskip.03cm x_i \dots x_n\hskip.03cm, & \ \text{if}\quad x_i \parallel x_{i+1}\hskip.03cm. \end{cases} \end{align} $$
5.2 Single-element ratio bounds
Let
![]() $P=(X,\prec )$
be a poset with
$P=(X,\prec )$
be a poset with
![]() $|X|=n$
elements, and fix an element
$|X|=n$
elements, and fix an element
![]() $a\in X$
of the poset. Let
$a\in X$
of the poset. Let
![]() $\mathcal {N}_k$
be the set of linear extensions
$\mathcal {N}_k$
be the set of linear extensions
![]() $L\in \mathcal {E}(P)$
such that
$L\in \mathcal {E}(P)$
such that
![]() $L(a)=k$
, and let
$L(a)=k$
, and let
![]() $\textrm {N}_k :=|\mathcal {N}_k|$
.
$\textrm {N}_k :=|\mathcal {N}_k|$
.
Lemma 5.1 We have
 $$\begin{align*}\begin{aligned} \frac{\mathrm{N}_{k}}{\mathrm{N}_{k-1}} \ &\leq \ t(a) \quad &&\text{if} \quad \mathrm{N}_{k-1}>0, \quad \text{and}\\ \frac{\mathrm{N}_{k}}{\mathrm{N}_{k+1}} \ &\leq \ t^*(a) \quad &&\text{if} \quad \mathrm{N}_{k+1}>0. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \frac{\mathrm{N}_{k}}{\mathrm{N}_{k-1}} \ &\leq \ t(a) \quad &&\text{if} \quad \mathrm{N}_{k-1}>0, \quad \text{and}\\ \frac{\mathrm{N}_{k}}{\mathrm{N}_{k+1}} \ &\leq \ t^*(a) \quad &&\text{if} \quad \mathrm{N}_{k+1}>0. \end{aligned} \end{align*}$$
The idea and basic setup of the proof will be used throughout.
Proof Consider the first inequality. The main idea is to construct an explicit injection
![]() $\phi : \mathcal {N}_k \to \mathcal {N}_{k-1} \times I$
, where
$\phi : \mathcal {N}_k \to \mathcal {N}_{k-1} \times I$
, where
![]() $I:= \{1,\ldots ,t(a)\}$
. This will show that
$I:= \{1,\ldots ,t(a)\}$
. This will show that
![]() $\textrm {N}_k = | \mathcal {N}_k | \leq | \mathcal {N}_{k-1} \times I | =\textrm {N}_{k-1} t(a)$
.
$\textrm {N}_k = | \mathcal {N}_k | \leq | \mathcal {N}_{k-1} \times I | =\textrm {N}_{k-1} t(a)$
.
We identify a linear extension L where
![]() $L(a)=k$
with a word
$L(a)=k$
with a word
![]() ${\mathbf{x}} \in \mathcal {N}_k$
where
${\mathbf{x}} \in \mathcal {N}_k$
where
![]() $x_k =a$
. Let
$x_k =a$
. Let
![]() $x_i$
be the last element in
$x_i$
be the last element in
![]() ${\mathbf{x}}$
appearing before a which is incomparable to a, that is, set
${\mathbf{x}}$
appearing before a which is incomparable to a, that is, set
![]() $i:=\max \hskip .03cm \{\hskip .03cm i \hskip .06cm : \hskip .06cm i <k, \hskip .06cm x_i \not \prec x_k \hskip .03cm\}$
. Such element exists because
$i:=\max \hskip .03cm \{\hskip .03cm i \hskip .06cm : \hskip .06cm i <k, \hskip .06cm x_i \not \prec x_k \hskip .03cm\}$
. Such element exists because
![]() $\textrm {N}_{k-1}>0$
implies that
$\textrm {N}_{k-1}>0$
implies that
![]() $b(a)\leq k-1$
and so among
$b(a)\leq k-1$
and so among
![]() $x_1,\ldots ,x_{k-1}$
there is at least one
$x_1,\ldots ,x_{k-1}$
there is at least one
![]() $x_i \not \prec a$
. Moreover, since i is maximal, we must have
$x_i \not \prec a$
. Moreover, since i is maximal, we must have
![]() $x_j \prec x_k$
for
$x_j \prec x_k$
for
![]() $j \in [i+1,k]$
. Also, for
$j \in [i+1,k]$
. Also, for
![]() $j\in [i+1,k]$
, we must have
$j\in [i+1,k]$
, we must have
![]() $x_j \hskip .03cm\|\hskip .03cm{} x_i$
, as otherwise we would have
$x_j \hskip .03cm\|\hskip .03cm{} x_i$
, as otherwise we would have
![]() $x_i \prec x_j \prec x_k=a$
. Thus, we have
$x_i \prec x_j \prec x_k=a$
. Thus, we have
![]() $x_j \in U(a,x_i)$
for
$x_j \in U(a,x_i)$
for
![]() $i <j<k$
and so
$i <j<k$
and so
![]() $1\leq k-i \leq t(a)$
.
$1\leq k-i \leq t(a)$
.
We now define
![]() $\phi ({\mathbf{x}}) := ({\mathbf{x}} \tau _i \cdots \tau _{k-1} , k-i)$
. Since
$\phi ({\mathbf{x}}) := ({\mathbf{x}} \tau _i \cdots \tau _{k-1} , k-i)$
. Since
![]() $x_i \hskip .03cm\|\hskip .03cm{} x_j$
for
$x_i \hskip .03cm\|\hskip .03cm{} x_j$
for
![]() $j\in [i+1,\ldots ,k]$
, we have that
$j\in [i+1,\ldots ,k]$
, we have that
![]() $x_i$
is transposed consecutively with
$x_i$
is transposed consecutively with
![]() $x_{i+1},\ldots ,x_k$
, so
$x_{i+1},\ldots ,x_k$
, so
![]() ${\mathbf{x}} \tau _i \cdots \tau _{k-1} = x_1\ldots x_{i-1}x_{i+1}\ldots x_k x_i x_{k+1}\ldots \in \mathcal {N}_{k-1}$
. We record the original position of
${\mathbf{x}} \tau _i \cdots \tau _{k-1} = x_1\ldots x_{i-1}x_{i+1}\ldots x_k x_i x_{k+1}\ldots \in \mathcal {N}_{k-1}$
. We record the original position of
![]() $x_i$
via
$x_i$
via
![]() $k-i$
.
$k-i$
.
To see this is an injection, we construct
![]() $\phi ^{-1}$
, if it exists. Namely,
$\phi ^{-1}$
, if it exists. Namely,
![]() $\phi ^{-1}({\mathbf{x}}',r)$
moves the element
$\phi ^{-1}({\mathbf{x}}',r)$
moves the element
![]() $x^{\prime }_k$
after
$x^{\prime }_k$
after
![]() $x^{\prime }_{k-1}=a$
forward by
$x^{\prime }_{k-1}=a$
forward by
![]() $r=(k-i)$
positions as long as
$r=(k-i)$
positions as long as
![]() $x^{\prime }_k \hskip .03cm\|\hskip .03cm{} x_j$
for
$x^{\prime }_k \hskip .03cm\|\hskip .03cm{} x_j$
for
![]() $j \in [k-r,k-1]$
. This completes the proof of the first inequality. The second inequality follows by applying the same argument to the dual poset
$j \in [k-r,k-1]$
. This completes the proof of the first inequality. The second inequality follows by applying the same argument to the dual poset
![]() $P^*$
.
$P^*$
.
Corollary 5.2 We have
 $$\begin{align*}\begin{aligned} \frac{\mathrm{N}_{k}}{\mathrm{N}_{k-1}} \ &\leq \ k-1 \quad &&\text{if} \quad \mathrm{N}_{k-1}>0, \quad \text{and}\\ \frac{\mathrm{N}_{k}}{\mathrm{N}_{k+1}} \ &\leq \ n-k \quad &&\text{if} \quad \mathrm{N}_{k+1}>0. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \frac{\mathrm{N}_{k}}{\mathrm{N}_{k-1}} \ &\leq \ k-1 \quad &&\text{if} \quad \mathrm{N}_{k-1}>0, \quad \text{and}\\ \frac{\mathrm{N}_{k}}{\mathrm{N}_{k+1}} \ &\leq \ n-k \quad &&\text{if} \quad \mathrm{N}_{k+1}>0. \end{aligned} \end{align*}$$
Note that the inequalities in the corollary are tight (see Proposition 7.4).
Proof Observe that
![]() $t(a) \leq k-1$
since there are at most
$t(a) \leq k-1$
since there are at most
![]() $(k-1)$
elements less than or equal to a by the assumption that
$(k-1)$
elements less than or equal to a by the assumption that
![]() $\textrm {N}_{k-1}>0$
. Similarly, observe that
$\textrm {N}_{k-1}>0$
. Similarly, observe that
![]() $t^*(a) \leq n-k$
since there are at most
$t^*(a) \leq n-k$
since there are at most
![]() $(n-k)$
elements greater than or equal to a by the assumption that
$(n-k)$
elements greater than or equal to a by the assumption that
![]() $\textrm {N}_{k+1}>0$
. These imply the result.
$\textrm {N}_{k+1}>0$
. These imply the result.
5.3 Double-element ratio bounds
We now give bounds for nonzero ratios of
![]() $\textrm {F}(k,\ell )$
. For the degenerate case, see Section 4.
$\textrm {F}(k,\ell )$
. For the degenerate case, see Section 4.
Lemma 5.3 Suppose that
![]() $\textrm {F}(k,\ell +2)>0$
. Then we have
$\textrm {F}(k,\ell +2)>0$
. Then we have
 $$ \begin{align*} \frac{ \mathrm{F}(k+1,\ell+1) }{\mathrm{F}(k,\ell+2)} \, \leq \, \min\{ t(z_2), k \} \, + \, \min\big\{ b(z_1,z_2)-2, t^*(z_1)\big\} \hskip.06cm \cdot \hskip.06cm \big( t^*(z_3) + t(z_2)\big). \end{align*} $$
$$ \begin{align*} \frac{ \mathrm{F}(k+1,\ell+1) }{\mathrm{F}(k,\ell+2)} \, \leq \, \min\{ t(z_2), k \} \, + \, \min\big\{ b(z_1,z_2)-2, t^*(z_1)\big\} \hskip.06cm \cdot \hskip.06cm \big( t^*(z_3) + t(z_2)\big). \end{align*} $$
Similarly, suppose that
![]() $\mathrm {F}(k+2,\ell )>0$
. Then we have
$\mathrm {F}(k+2,\ell )>0$
. Then we have
 $$ \begin{align*} \frac{ \mathrm{F}(k+1,\ell+1) }{\mathrm{F}(k+2,\ell)} \, \leq \, \min\big\{ t^*(z_2), \ell \big\} \, + \, \min\big\{ b(z_2,z_3)-2,t(z_3)\big\} \hskip.06cm \cdot \hskip.06cm \big( t(z_1) + t^*(z_2)\big). \end{align*} $$
$$ \begin{align*} \frac{ \mathrm{F}(k+1,\ell+1) }{\mathrm{F}(k+2,\ell)} \, \leq \, \min\big\{ t^*(z_2), \ell \big\} \, + \, \min\big\{ b(z_2,z_3)-2,t(z_3)\big\} \hskip.06cm \cdot \hskip.06cm \big( t(z_1) + t^*(z_2)\big). \end{align*} $$
Proof For the first inequality, we construct an injection
![]() $\psi : \mathcal F(k+1,\ell +1) \to I \times \mathcal F(k+2,\ell )$
, where
$\psi : \mathcal F(k+1,\ell +1) \to I \times \mathcal F(k+2,\ell )$
, where
![]() $I=I_1 \sqcup I_2 \sqcup I_3$
and
$I=I_1 \sqcup I_2 \sqcup I_3$
and
![]() $I_i$
are intervals of lengths given by the RHS (see below). We use notation
$I_i$
are intervals of lengths given by the RHS (see below). We use notation
![]() $[p,q]=\{i\in \mathbb N \hskip .06cm : \hskip .06cm p \le i \le q\}$
to denote the integer interval.
$[p,q]=\{i\in \mathbb N \hskip .06cm : \hskip .06cm p \le i \le q\}$
to denote the integer interval.
Let
![]() ${\mathbf{x}} \in \mathcal F(k+1,\ell +1)$
be a word, such that
${\mathbf{x}} \in \mathcal F(k+1,\ell +1)$
be a word, such that
![]() $x_i=z_1$
,
$x_i=z_1$
,
![]() $x_{i+k+1} =z_2$
and
$x_{i+k+1} =z_2$
and
![]() $x_{i+k+\ell +2} =z_3$
. We consider several cases.
$x_{i+k+\ell +2} =z_3$
. We consider several cases.
Case 1: Suppose there exists an element
![]() $x_j \not \prec z_2$
for some
$x_j \not \prec z_2$
for some
![]() $j \in [i+1,i+k]$
. Let j be the maximal such index. Then, for every
$j \in [i+1,i+k]$
. Let j be the maximal such index. Then, for every
![]() $r \in [j+1,i+k]$
, we have that
$r \in [j+1,i+k]$
, we have that
![]() $x_r \in U(z_2,x_j)$
. Set
$x_r \in U(z_2,x_j)$
. Set
![]() $\psi ({\mathbf{x}}) = ({\mathbf{x}} \tau _j \cdots \tau _{i+k}, i+k+1-j)$
, i.e.,
$\psi ({\mathbf{x}}) = ({\mathbf{x}} \tau _j \cdots \tau _{i+k}, i+k+1-j)$
, i.e.,
![]() $\psi $
moves
$\psi $
moves
![]() $x_j$
to the position after
$x_j$
to the position after
![]() $z_2$
, so that
$z_2$
, so that
![]() $z_2$
is now in position
$z_2$
is now in position
![]() $\hskip .03cm i+k$
. Observe that the inverse of
$\hskip .03cm i+k$
. Observe that the inverse of
![]() $\hskip .03cm \psi $
exists for all
$\hskip .03cm \psi $
exists for all
![]() ${\mathbf{y}} \in \mathcal F(k,\ell +2)$
, since
${\mathbf{y}} \in \mathcal F(k,\ell +2)$
, since
![]() $y_{i+k}=z_2\hskip .03cm\|\hskip .03cm{}y_{i+k+1}$
. Note that
$y_{i+k}=z_2\hskip .03cm\|\hskip .03cm{}y_{i+k+1}$
. Note that
![]() $i+k+1-j \leq \min \{ u(z_2,x_j), k \}$
. Thus, we can record the value
$i+k+1-j \leq \min \{ u(z_2,x_j), k \}$
. Thus, we can record the value
![]() $(i+k+1-j)$
in the first interval
$(i+k+1-j)$
in the first interval
![]() $I_1 =[1, \min \{t(z_2),k\}]$
.
$I_1 =[1, \min \{t(z_2),k\}]$
.
Case 2: Suppose that we have
![]() $x_j \prec z_2$
for all
$x_j \prec z_2$
for all
![]() $j\in [i,i+k]$
. Then there exists an element
$j\in [i,i+k]$
. Then there exists an element
![]() $x_j \not \succ z_1$
. Indeed, otherwise
$x_j \not \succ z_1$
. Indeed, otherwise
![]() $x_j \in B(z_1,z_2)$
for all
$x_j \in B(z_1,z_2)$
for all
![]() $j \in [i,i+k+1]$
, which gives
$j \in [i,i+k+1]$
, which gives
![]() $k+2 \leq |B(z_1,z_2)|$
and implies
$k+2 \leq |B(z_1,z_2)|$
and implies
![]() $\textrm {F}(k,\ell +2)=0$
contradicting the assumption. As above, let j be the smallest possible index such that
$\textrm {F}(k,\ell +2)=0$
contradicting the assumption. As above, let j be the smallest possible index such that
![]() $x_j\hskip .03cm\|\hskip .03cm{}z_1$
, so we can move
$x_j\hskip .03cm\|\hskip .03cm{}z_1$
, so we can move
![]() $x_j$
in front of
$x_j$
in front of
![]() $z_1$
. Note that
$z_1$
. Note that
![]() $j-i \leq \min \{ b(z_1,z_2)-2, u^*(z_1,x_j)\}$
. We now have a word
$j-i \leq \min \{ b(z_1,z_2)-2, u^*(z_1,x_j)\}$
. We now have a word
![]() ${\mathbf{x}}' \in \mathcal F(k,\ell +1)$
. We split this case into two subcases.
${\mathbf{x}}' \in \mathcal F(k,\ell +1)$
. We split this case into two subcases.
Subcase 2.1: Suppose there exists
![]() $x_r \not \succ z_3$
for
$x_r \not \succ z_3$
for
![]() $r> i+k+\ell +2$
. Let r be the minimal such index, and move
$r> i+k+\ell +2$
. Let r be the minimal such index, and move
![]() $x_r$
in front of
$x_r$
in front of
![]() $z_3$
, creating a word
$z_3$
, creating a word
![]() ${\mathbf{x}}" \in \mathcal F(k,\ell +2)$
. Note that
${\mathbf{x}}" \in \mathcal F(k,\ell +2)$
. Note that
![]() $r-(k+\ell +2+i) \leq u^*(z_3,x_r)$
. Thus, we can record the value
$r-(k+\ell +2+i) \leq u^*(z_3,x_r)$
. Thus, we can record the value
![]() $(j-i,r-(k+\ell +2+i))$
in the second interval
$(j-i,r-(k+\ell +2+i))$
in the second interval
![]() $I_2=[1,\min \{ b(z_1,z_2)-2, t^*(z_1)\}t^*(z_3)]$
.
$I_2=[1,\min \{ b(z_1,z_2)-2, t^*(z_1)\}t^*(z_3)]$
.
Subcase 2.2: Suppose
![]() $x_s \succ z_3$
for all
$x_s \succ z_3$
for all
![]() $s> i+k+\ell +2$
. Then, since
$s> i+k+\ell +2$
. Then, since
![]() $\textrm {F}(k,\ell +2) \neq 0$
, there must be some
$\textrm {F}(k,\ell +2) \neq 0$
, there must be some
![]() $x_s \not \prec z_2$
, for
$x_s \not \prec z_2$
, for
![]() $s< i+k+1$
. Since we are in Case 2, we have
$s< i+k+1$
. Since we are in Case 2, we have
![]() $s< i$
. Let s be the largest such index. Thus,
$s< i$
. Let s be the largest such index. Thus,
![]() $x_{s+1},\ldots ,x_{i+k} \prec x_{i+k+1}= z_2$
. We can then move
$x_{s+1},\ldots ,x_{i+k} \prec x_{i+k+1}= z_2$
. We can then move
![]() $x_s$
past all these entries to right past
$x_s$
past all these entries to right past
![]() $z_2$
and obtain a word in
$z_2$
and obtain a word in
![]() $\mathcal F(k,\ell +2)$
. Note that
$\mathcal F(k,\ell +2)$
. Note that
![]() $i-s \leq u(z_2,x_s)$
. Thus, we can record the value
$i-s \leq u(z_2,x_s)$
. Thus, we can record the value
![]() $(j-i, i-s)$
in the third interval
$(j-i, i-s)$
in the third interval
![]() $I_3=[\min \{ b(z_1,z_2)-2, t^*(z_1)\} t(z_2)]$
.
$I_3=[\min \{ b(z_1,z_2)-2, t^*(z_1)\} t(z_2)]$
.
Gathering these cases, and noting that
![]() $t(x) \geq u(x,y)$
and
$t(x) \geq u(x,y)$
and
![]() $t^*(x) \geq u^*(x,y)$
for all
$t^*(x) \geq u^*(x,y)$
for all
![]() $x,y\in X$
, we obtain the desired first inequality. For the second inequality, we apply the analogous argument to the dual poset
$x,y\in X$
, we obtain the desired first inequality. For the second inequality, we apply the analogous argument to the dual poset
![]() $P^*$
.
$P^*$
.
5.4 Bounds on cross-product ratios
We can now bound the cross-product ratios in the nonvanishing case.
Corollary 5.4 Let
![]() $P=(X,\prec )$
be either a t-thin or t-flat poset with respect to
$P=(X,\prec )$
be either a t-thin or t-flat poset with respect to
![]() $\{z_1,z_2,z_3\}$
. Suppose that
$\{z_1,z_2,z_3\}$
. Suppose that
![]() $\textrm {F}(k,\ell +2)>0$
. Then we have
$\textrm {F}(k,\ell +2)>0$
. Then we have
Similarly, suppose that
![]() $\textrm {F}(k+2,\ell )>0$
. Then we have
$\textrm {F}(k+2,\ell )>0$
. Then we have
Proof These inequalities come from different choices in the minima on the RHS of inequalities in Lemma 5.3.
Theorem 5.5 Let
![]() $P=(X,\prec )$
be either a t-thin or t-flat poset with respect to
$P=(X,\prec )$
be either a t-thin or t-flat poset with respect to
![]() $\{z_1,z_2,z_3\}$
. Suppose also that
$\{z_1,z_2,z_3\}$
. Suppose also that
![]() $\textrm {F}(k,\ell +2) \hskip .06cm \textrm {F}(k+2,\ell )>0$
. Then
$\textrm {F}(k,\ell +2) \hskip .06cm \textrm {F}(k+2,\ell )>0$
. Then
 $$ \begin{align*} \frac{\mathrm{F}(k+1,\ell)\mathrm{F}(k,\ell+1)}{\mathrm{F}(k,\ell)\mathrm{F}(k+1,\ell+1)} \ \geq \ \max \left\{\frac{1}{2} \, + \, \frac{1}{2\hskip.03cm \sqrt{k\ell} \hskip.03cm (2t+1)} \ , \, \frac{1}{2} \, + \,\frac{1}{2 \hskip.03cm (2t^2+t)}\right\}. \end{align*} $$
$$ \begin{align*} \frac{\mathrm{F}(k+1,\ell)\mathrm{F}(k,\ell+1)}{\mathrm{F}(k,\ell)\mathrm{F}(k+1,\ell+1)} \ \geq \ \max \left\{\frac{1}{2} \, + \, \frac{1}{2\hskip.03cm \sqrt{k\ell} \hskip.03cm (2t+1)} \ , \, \frac{1}{2} \, + \,\frac{1}{2 \hskip.03cm (2t^2+t)}\right\}. \end{align*} $$
Theorem 5.6 Suppose that
![]() $\textrm {F}(k,\ell +2) \hskip .06cm \textrm {F}(k+2,\ell )> 0$
. Then
$\textrm {F}(k,\ell +2) \hskip .06cm \textrm {F}(k+2,\ell )> 0$
. Then
 $$ \begin{align*}{\mathrm{F}(k+1,\ell)\hskip.06cm \mathrm{F}(k,\ell+1)} \, &\geq \, {\mathrm{F}(k,\ell) \hskip.06cm \mathrm{F}(k+1,\ell+1)}\\ &\bigg( \frac12 \, + \, \frac{1}{2 \hskip.03cm \sqrt{(2nk-2n-k+2)(2n\ell-2n-\ell+2)} }\bigg).\end{align*} $$
$$ \begin{align*}{\mathrm{F}(k+1,\ell)\hskip.06cm \mathrm{F}(k,\ell+1)} \, &\geq \, {\mathrm{F}(k,\ell) \hskip.06cm \mathrm{F}(k+1,\ell+1)}\\ &\bigg( \frac12 \, + \, \frac{1}{2 \hskip.03cm \sqrt{(2nk-2n-k+2)(2n\ell-2n-\ell+2)} }\bigg).\end{align*} $$
Proof It follows from the definition that
![]() $t(x), t^*(x) \leq n-1$
for every
$t(x), t^*(x) \leq n-1$
for every
![]() $x \in X$
. The nonvanishing condition in the assumption, combined with Theorem 4.2 implies that
$x \in X$
. The nonvanishing condition in the assumption, combined with Theorem 4.2 implies that
![]() $b(z_1,z_2)\leq k+1$
and
$b(z_1,z_2)\leq k+1$
and
![]() $b(z_2,z_3) \leq \ell +1$
. It then follows from Lemma 5.3 that
$b(z_2,z_3) \leq \ell +1$
. It then follows from Lemma 5.3 that
 $$\begin{align*}\frac{ \textrm{F}(k+1,\ell+1) }{\textrm{F}(k,\ell+2)} \ \leq \ k+(k-1) (2t) \ \leq \ k+(k-1)(2n-2) \ = \ 2nk-2n-k+2.\end{align*}$$
$$\begin{align*}\frac{ \textrm{F}(k+1,\ell+1) }{\textrm{F}(k,\ell+2)} \ \leq \ k+(k-1) (2t) \ \leq \ k+(k-1)(2n-2) \ = \ 2nk-2n-k+2.\end{align*}$$
Similarly, we have
The theorem now follows from Proposition 3.3.
6 Cross-product inequalities in the vanishing case
6.1 Double-element ratio bounds
As before, let
![]() $P=(X,\prec )$
be a poset with
$P=(X,\prec )$
be a poset with
![]() $|X|=n$
elements, and let
$|X|=n$
elements, and let
![]() $z_1\prec z_2 \prec z_3$
be distinct elements in X. The following are the counterparts of the cross-product inequalities in Section 5.3.
$z_1\prec z_2 \prec z_3$
be distinct elements in X. The following are the counterparts of the cross-product inequalities in Section 5.3.
Lemma 6.1 Suppose that
![]() $\textrm {F}(k,\ell )> 0$
. Then
$\textrm {F}(k,\ell )> 0$
. Then
 $$ \begin{align*} & \frac{\mathrm{F}(k+1,\ell)}{\mathrm{F}(k,\ell)} \ \leq \ \min\{ k, t^*(z_1)\} \, +\, \min\{k, t(z_3)-1\}\, +\, \\ & \qquad + \, \min\{b(z_1,z_2)-1,t(z_2)\} \hskip.06cm \big(\min\{\ell-1,t(z_3)\} + \min\{\ell-1,t^*(z_1)-1\}\big). \end{align*} $$
$$ \begin{align*} & \frac{\mathrm{F}(k+1,\ell)}{\mathrm{F}(k,\ell)} \ \leq \ \min\{ k, t^*(z_1)\} \, +\, \min\{k, t(z_3)-1\}\, +\, \\ & \qquad + \, \min\{b(z_1,z_2)-1,t(z_2)\} \hskip.06cm \big(\min\{\ell-1,t(z_3)\} + \min\{\ell-1,t^*(z_1)-1\}\big). \end{align*} $$
Note that the nonvanishing condition implies that
![]() $b(z_1,z_2)\leq k+1$
and
$b(z_1,z_2)\leq k+1$
and
![]() $b(z_2,z_3) \leq \ell +1$
.
$b(z_2,z_3) \leq \ell +1$
.
Proof We proceed as in the proof of Lemma 5.3, constructing an injection
![]() $\psi : \mathcal F(k+1,\ell ) \to I \times \mathcal F(k,\ell )$
, where
$\psi : \mathcal F(k+1,\ell ) \to I \times \mathcal F(k,\ell )$
, where
![]() $I=I_1\sqcup I_2 \sqcup I_{3} \sqcup I_4$
are intervals of lengths specified by the RHS, each of them given in the corresponding case below.
$I=I_1\sqcup I_2 \sqcup I_{3} \sqcup I_4$
are intervals of lengths specified by the RHS, each of them given in the corresponding case below.
Let
![]() ${\boldsymbol{x}} \in \mathcal F(k+1,\ell )$
be a word (corresponding to a linear extension) with
${\boldsymbol{x}} \in \mathcal F(k+1,\ell )$
be a word (corresponding to a linear extension) with
![]() $x_i=z_1$
,
$x_i=z_1$
,
![]() $x_{i+k+1}=z_2$
and
$x_{i+k+1}=z_2$
and
![]() $x_{i+k+\ell +1}=z_3$
. We consider several independent cases, which correspond to different parts of the interval I:
$x_{i+k+\ell +1}=z_3$
. We consider several independent cases, which correspond to different parts of the interval I:
Case 1: Suppose that there exists
![]() $x_j \hskip .03cm\|\hskip .03cm{} z_1$
with
$x_j \hskip .03cm\|\hskip .03cm{} z_1$
with
![]() $j \in [i+1,i+k]$
and let j be the minimal such index. Then
$j \in [i+1,i+k]$
and let j be the minimal such index. Then
![]() $\{x_i,\ldots ,x_{j-1}\} \subseteq U^*(z_1,x_j)$
and
$\{x_i,\ldots ,x_{j-1}\} \subseteq U^*(z_1,x_j)$
and
![]() $j-i \leq \min \{k,t^*(z_1)\}$
. Take
$j-i \leq \min \{k,t^*(z_1)\}$
. Take
![]() ${\boldsymbol{x}} \tau _{j-1} \cdots \tau _i$
, which moves
${\boldsymbol{x}} \tau _{j-1} \cdots \tau _i$
, which moves
![]() $x_j$
to position i and
$x_j$
to position i and
![]() $z_1$
to position
$z_1$
to position
![]() $i+1$
. Then the resulting word is in
$i+1$
. Then the resulting word is in
![]() $\mathcal F(k,\ell )$
, and we record the value
$\mathcal F(k,\ell )$
, and we record the value
![]() $(j-i)$
in the first interval
$(j-i)$
in the first interval
![]() $I_1=[1,\min \{ k, t^*(z_1)\}]$
.
$I_1=[1,\min \{ k, t^*(z_1)\}]$
.
Case 2: Suppose that
![]() $x_j \succ z_1$
for all
$x_j \succ z_1$
for all
![]() $j \in [i+1,i+k]$
. Furthermore, suppose that
$j \in [i+1,i+k]$
. Furthermore, suppose that
![]() $x_r \succ z_1$
and
$x_r \succ z_1$
and
![]() $x_r \prec z_3$
for all
$x_r \prec z_3$
for all
![]() $r \in [i+k+2,i+k+\ell ]$
. These assumptions imply that there exists
$r \in [i+k+2,i+k+\ell ]$
. These assumptions imply that there exists
![]() $j \in [i+1,i+k]$
such that
$j \in [i+1,i+k]$
such that
![]() $x_j\hskip .03cm\|\hskip .03cm{} z_3$
, as otherwise we have
$x_j\hskip .03cm\|\hskip .03cm{} z_3$
, as otherwise we have
![]() $\{x_{i}, \ldots , x_{i+k+\ell +1}\} \in B(z_1,z_3)$
, contradicting the assumption that
$\{x_{i}, \ldots , x_{i+k+\ell +1}\} \in B(z_1,z_3)$
, contradicting the assumption that
![]() $\textrm {F}(k,\ell )>0$
. Assume that j is the maximal such index j. It then follows that
$\textrm {F}(k,\ell )>0$
. Assume that j is the maximal such index j. It then follows that
![]() $\{x_{j+1},\ldots , x_{i+k+\ell +1}\} \subseteq U(z_3,x_j) $
. This implies that
$\{x_{j+1},\ldots , x_{i+k+\ell +1}\} \subseteq U(z_3,x_j) $
. This implies that
![]() $i+k+\ell +1-j \leq t(z_3)$
, which in turn implies that
$i+k+\ell +1-j \leq t(z_3)$
, which in turn implies that
![]() $i+k+1-j\leq t(z_3)-\ell \leq t(z_3)-1$
. Then we take
$i+k+1-j\leq t(z_3)-\ell \leq t(z_3)-1$
. Then we take
![]() ${\boldsymbol{x}}' = {\boldsymbol{x}} \tau _{j}\cdots \tau _{i+k+\ell +1} \in \mathcal F(k,\ell )$
and record the value
${\boldsymbol{x}}' = {\boldsymbol{x}} \tau _{j}\cdots \tau _{i+k+\ell +1} \in \mathcal F(k,\ell )$
and record the value
![]() $(i+k+1-j)$
in the second interval
$(i+k+1-j)$
in the second interval
![]() $I_2=[1,\min \{k, t(z_3)-1\}]$
.
$I_2=[1,\min \{k, t(z_3)-1\}]$
.
Case 3: Suppose again that
![]() $x_j \succ z_1$
for all
$x_j \succ z_1$
for all
![]() $j \in [i+1,i+k]$
, but now that there exists
$j \in [i+1,i+k]$
, but now that there exists
![]() $r \in [i+k+2,i+k+\ell ]$
such that either
$r \in [i+k+2,i+k+\ell ]$
such that either
![]() $x_r \hskip .03cm\|\hskip .03cm{} z_1$
or
$x_r \hskip .03cm\|\hskip .03cm{} z_1$
or
![]() $x_r \hskip .03cm\|\hskip .03cm{} z_3$
. The first condition implies that there exists
$x_r \hskip .03cm\|\hskip .03cm{} z_3$
. The first condition implies that there exists
![]() $x_j \hskip .03cm\|\hskip .03cm{}z_2$
with
$x_j \hskip .03cm\|\hskip .03cm{}z_2$
with
![]() $j\in [i+1,i+k]$
, as otherwise we would have
$j\in [i+1,i+k]$
, as otherwise we would have
![]() $\textrm {F}(k,\ell )=0$
. Let j be the maximal such index. Then
$\textrm {F}(k,\ell )=0$
. Let j be the maximal such index. Then
![]() $\{x_{j+1},\ldots ,x_{i+k+1} \} \subseteq B(z_1,z_2)-z_1$
, and thus
$\{x_{j+1},\ldots ,x_{i+k+1} \} \subseteq B(z_1,z_2)-z_1$
, and thus
![]() $i+k+1-j \leq b(z_1,z_2)-1$
. Also, note that
$i+k+1-j \leq b(z_1,z_2)-1$
. Also, note that
![]() $\{x_{j+1},\ldots ,x_{i+k+1} \} \subseteq U(z_2,x_j)$
, and thus
$\{x_{j+1},\ldots ,x_{i+k+1} \} \subseteq U(z_2,x_j)$
, and thus
![]() $i+k+1-j \leq t(z_2)$
. Move
$i+k+1-j \leq t(z_2)$
. Move
![]() $x_j$
right past
$x_j$
right past
![]() $z_2$
via
$z_2$
via
![]() ${\boldsymbol{x}} \tau _j \cdots \tau _{i+k+1}$
and record that move with
${\boldsymbol{x}} \tau _j \cdots \tau _{i+k+1}$
and record that move with
![]() $s:=i+k+1-j \leq \min \{b(z_1,z_2)-1,t(z_2)\}$
. We now consider the new word
$s:=i+k+1-j \leq \min \{b(z_1,z_2)-1,t(z_2)\}$
. We now consider the new word
![]() ${\mathbf{x}}' \in \mathcal F(k,\ell +1)$
. We split this case into two subcases.
${\mathbf{x}}' \in \mathcal F(k,\ell +1)$
. We split this case into two subcases.
Subcase 3.1: Suppose that there exists an element
![]() $x_r'=x_r \hskip .03cm\|\hskip .03cm{}z_3$
for some
$x_r'=x_r \hskip .03cm\|\hskip .03cm{}z_3$
for some
![]() $r \in [i+k+2,i+k+\ell ]$
. Let r be the maximal such index. Then
$r \in [i+k+2,i+k+\ell ]$
. Let r be the maximal such index. Then
![]() $\{ x^{\prime }_{r+1},\ldots ,x^{\prime }_{i+k+\ell +1} \} \subseteq U(z_3,x^{\prime }_r)$
and
$\{ x^{\prime }_{r+1},\ldots ,x^{\prime }_{i+k+\ell +1} \} \subseteq U(z_3,x^{\prime }_r)$
and
![]() $i+k+\ell +1-r \leq t(z_3)$
. We then create the word
$i+k+\ell +1-r \leq t(z_3)$
. We then create the word
![]() ${\boldsymbol{x}}' \tau _r \cdots \tau _{i+k+\ell +1}\in \mathcal F(k,\ell )$
where
${\boldsymbol{x}}' \tau _r \cdots \tau _{i+k+\ell +1}\in \mathcal F(k,\ell )$
where
![]() $x^{\prime }_r$
is moved past
$x^{\prime }_r$
is moved past
![]() $z_3$
. We record the pair
$z_3$
. We record the pair
![]() $(s,i+k+\ell +1-r)$
in the product of intervals
$(s,i+k+\ell +1-r)$
in the product of intervals
![]() $I_3=[1,\min \{b(z_1,z_2)-1,t(z_2)\}] \times [1,\min \{\ell -1,t(z_3)\}]$
.
$I_3=[1,\min \{b(z_1,z_2)-1,t(z_2)\}] \times [1,\min \{\ell -1,t(z_3)\}]$
.
Subcase 3.2: Suppose that there exists
![]() $x_r'=x_r \hskip .03cm\|\hskip .03cm{}z_1$
for
$x_r'=x_r \hskip .03cm\|\hskip .03cm{}z_1$
for
![]() $r \in [i+k+2,i+k+\ell ]$
. We take the minimal such r. Then
$r \in [i+k+2,i+k+\ell ]$
. We take the minimal such r. Then
![]() $\{x^{\prime }_{i},\ldots , x^{\prime }_{r-1}\} \subseteq U^*(z_1, x_r')$
and thus
$\{x^{\prime }_{i},\ldots , x^{\prime }_{r-1}\} \subseteq U^*(z_1, x_r')$
and thus
![]() $r-i\leq t^*(z_1)$
. This in turn implies that
$r-i\leq t^*(z_1)$
. This in turn implies that
![]() $r-i-k-1\kern1.3pt{\leq}\kern1.3pt t^*(z_1)\kern1.3pt{-}\kern1.3ptk\kern1.3pt{-}\kern1.3pt1 \kern1.3pt{\leq}\kern1.3pt t^*(z_1)\kern1.3pt{-}\kern1.3pt1$
. Take a word
$r-i-k-1\kern1.3pt{\leq}\kern1.3pt t^*(z_1)\kern1.3pt{-}\kern1.3ptk\kern1.3pt{-}\kern1.3pt1 \kern1.3pt{\leq}\kern1.3pt t^*(z_1)\kern1.3pt{-}\kern1.3pt1$
. Take a word
![]() ${\boldsymbol{x}}"\in \mathcal F(k,\ell )$
by moving
${\boldsymbol{x}}"\in \mathcal F(k,\ell )$
by moving
![]() $x_r'$
to the position before
$x_r'$
to the position before
![]() $z_1$
and record the pair
$z_1$
and record the pair
![]() $(s,r-i-k-1)$
in the product of intervals
$(s,r-i-k-1)$
in the product of intervals
![]() $I_4=[1,\min \{b(z_1,z_2)-1,t(z_2)\}] \times [1,\min \{\ell -1,t^*(z_1)-1\}]$
.
$I_4=[1,\min \{b(z_1,z_2)-1,t(z_2)\}] \times [1,\min \{\ell -1,t^*(z_1)-1\}]$
.
Gathering these cases, we obtain the desired inequality in the lemma.
Lemma 6.2 Suppose that
![]() $\textrm {F}(k+2,\ell )> 0$
. Then,
$\textrm {F}(k+2,\ell )> 0$
. Then,
 $$ \begin{align*}\frac{\mathrm{F}(k+1,\ell)}{\mathrm{F}(k+2,\ell)} \ \leq \ t(z_1) \hskip.06cm + \hskip.06cm \big(t^*(z_2)-1\big) \hskip.06cm + \hskip.06cm \min\big\{\ell-1,t^*(z_2)\big\} \hskip.06cm t^*(z_3).\end{align*} $$
$$ \begin{align*}\frac{\mathrm{F}(k+1,\ell)}{\mathrm{F}(k+2,\ell)} \ \leq \ t(z_1) \hskip.06cm + \hskip.06cm \big(t^*(z_2)-1\big) \hskip.06cm + \hskip.06cm \min\big\{\ell-1,t^*(z_2)\big\} \hskip.06cm t^*(z_3).\end{align*} $$
Proof We proceed as in the proof of Lemma 5.3, constructing an injection
![]() $\psi : \mathcal F(k+1,\ell ) \to I \times \mathcal F(k+2,\ell )$
, where
$\psi : \mathcal F(k+1,\ell ) \to I \times \mathcal F(k+2,\ell )$
, where
![]() $I=I_1\sqcup I_2 \sqcup I_{3}$
are intervals of lengths specified by the RHS corresponding to each case below.
$I=I_1\sqcup I_2 \sqcup I_{3}$
are intervals of lengths specified by the RHS corresponding to each case below.
Let
![]() ${\boldsymbol{x}} \in \mathcal F(k+1,\ell )$
be a word (corresponding to a linear extension) with
${\boldsymbol{x}} \in \mathcal F(k+1,\ell )$
be a word (corresponding to a linear extension) with
![]() $x_i=z_1$
,
$x_i=z_1$
,
![]() $x_{i+k+1}=z_2$
and
$x_{i+k+1}=z_2$
and
![]() $x_{i+k+\ell +1}=z_3$
. We consider three independent cases, which correspond to different intervals
$x_{i+k+\ell +1}=z_3$
. We consider three independent cases, which correspond to different intervals
![]() $I_i$
(see below).
$I_i$
(see below).
Case 1: Suppose that there exists
![]() $x_j \hskip .03cm\|\hskip .03cm{} z_1$
with
$x_j \hskip .03cm\|\hskip .03cm{} z_1$
with
![]() $j \in [1,i-1]$
, and let j be the maximal such index. Then
$j \in [1,i-1]$
, and let j be the maximal such index. Then
![]() $\{x_{j+1},\ldots ,x_{i}\} \subset U(z_1,x_j)$
and so
$\{x_{j+1},\ldots ,x_{i}\} \subset U(z_1,x_j)$
and so
![]() $i-j \leq t(z_1)$
. We take
$i-j \leq t(z_1)$
. We take
![]() ${\boldsymbol{x}} \tau _{j} \cdots \tau _{i-1}$
, which moves
${\boldsymbol{x}} \tau _{j} \cdots \tau _{i-1}$
, which moves
![]() $x_j$
to position i and
$x_j$
to position i and
![]() $z_1$
to position
$z_1$
to position
![]() $i-1$
. Then the resulting word is in
$i-1$
. Then the resulting word is in
![]() $\mathcal F(k+2,\ell )$
, and we record the value
$\mathcal F(k+2,\ell )$
, and we record the value
![]() $(i-j)$
in the first interval
$(i-j)$
in the first interval
![]() $I_1=[1,t(z_1)]$
.
$I_1=[1,t(z_1)]$
.
Case 2: Suppose that
![]() $x_j \prec z_1$
for all
$x_j \prec z_1$
for all
![]() $j \in [1,i-1]$
. Since
$j \in [1,i-1]$
. Since
![]() $\textrm {F}(k+2,\ell )>0$
, there exists
$\textrm {F}(k+2,\ell )>0$
, there exists
![]() $x_j \hskip .03cm\|\hskip .03cm{} z_2$
with
$x_j \hskip .03cm\|\hskip .03cm{} z_2$
with
![]() $j \in [ i+k+2,n]$
. Let j be the minimal such index. Then
$j \in [ i+k+2,n]$
. Let j be the minimal such index. Then
![]() $\{x_{i+k+1},\ldots ,x_{j-1} \} \subset U^*(z_2,x_j)$
, and thus
$\{x_{i+k+1},\ldots ,x_{j-1} \} \subset U^*(z_2,x_j)$
, and thus
![]() $j-i-k-1 \leq t^*(z_2)$
. Move
$j-i-k-1 \leq t^*(z_2)$
. Move
![]() $x_j$
to the front of
$x_j$
to the front of
![]() $z_2$
via
$z_2$
via
![]() ${\boldsymbol{x}} \tau _{j-1} \cdots \tau _{i+k+1}$
to get a new word
${\boldsymbol{x}} \tau _{j-1} \cdots \tau _{i+k+1}$
to get a new word
![]() $\hskip .03cm{\boldsymbol{x}}'$
. We split this case into two subcases:
$\hskip .03cm{\boldsymbol{x}}'$
. We split this case into two subcases:
Subcase 2.1: Suppose that
![]() $j \in [i+k+\ell +2,n]$
. Then
$j \in [i+k+\ell +2,n]$
. Then
![]() ${\boldsymbol{x}}' \in \mathcal F(k+2,\ell )$
. Also note that
${\boldsymbol{x}}' \in \mathcal F(k+2,\ell )$
. Also note that
![]() $j-i-k-\ell -1 \leq t^*(z_2)-\ell \leq t^*(z_2)-1$
. We then record the value
$j-i-k-\ell -1 \leq t^*(z_2)-\ell \leq t^*(z_2)-1$
. We then record the value
![]() $(j-i-k-\ell -1)$
in the second interval
$(j-i-k-\ell -1)$
in the second interval
![]() $I_2=[1,t^*(z_2)-1]$
.
$I_2=[1,t^*(z_2)-1]$
.
Subcase 2.2: Suppose that
![]() $j \in [i+k+2,i+k+\ell ]$
. Then
$j \in [i+k+2,i+k+\ell ]$
. Then
![]() ${\boldsymbol{x}}' \in \mathcal F(k+2,\ell -1)$
. By the assumption of Case 2 and the fact that
${\boldsymbol{x}}' \in \mathcal F(k+2,\ell -1)$
. By the assumption of Case 2 and the fact that
![]() $\textrm {F}(k+2,\ell )>0$
, there exists
$\textrm {F}(k+2,\ell )>0$
, there exists
![]() $r \in [i+k+\ell +2,n]$
such that
$r \in [i+k+\ell +2,n]$
such that
![]() $x_r' \hskip .03cm\|\hskip .03cm{} z_3$
. Assume that r is the minimal such index. It then follows that
$x_r' \hskip .03cm\|\hskip .03cm{} z_3$
. Assume that r is the minimal such index. It then follows that
![]() $\{x^{\prime }_{i+k+\ell +1},\ldots , x^{\prime }_{r-1}\} \subseteq U^*(z_3,x_r')$
. This implies that
$\{x^{\prime }_{i+k+\ell +1},\ldots , x^{\prime }_{r-1}\} \subseteq U^*(z_3,x_r')$
. This implies that
![]() $(r-i-k-\ell -1) \leq t^*(z_3)$
. Move
$(r-i-k-\ell -1) \leq t^*(z_3)$
. Move
![]() $x_r'$
to the front of
$x_r'$
to the front of
![]() $z_3$
to obtain a new word
$z_3$
to obtain a new word
![]() ${\boldsymbol{x}}" \in \mathcal F(k+2,\ell )$
, and we record the value
${\boldsymbol{x}}" \in \mathcal F(k+2,\ell )$
, and we record the value
![]() $(j-i-k-1,r-i-k-\ell -1)$
to the product of intervals
$(j-i-k-1,r-i-k-\ell -1)$
to the product of intervals
![]() $I_3 = [1,\min \{\ell -1,t^*(z_2)\}] \times [1,t^*(z_3)] $
.
$I_3 = [1,\min \{\ell -1,t^*(z_2)\}] \times [1,t^*(z_3)] $
.
Gathering these cases, we obtain the desired inequality in the lemma.
6.2 Bounds on cross-product ratios
We are now ready to obtain bounds on the cross-product ratios in the vanishing case.
Proposition 6.3 Suppose that
![]() $\textrm {F}(k,\ell ) \hskip .06cm \textrm {F}(k+2,\ell )> 0$
. Then
$\textrm {F}(k,\ell ) \hskip .06cm \textrm {F}(k+2,\ell )> 0$
. Then
 $$ \begin{align*}\frac{ \mathrm{F}(k,\ell) \hskip.06cm \mathrm{F}(k+2,\ell)}{\mathrm{F}(k+1,\ell)^2} \ \geq \ \frac{1}{2n\ell^2 k}\hskip.06cm. \end{align*} $$
$$ \begin{align*}\frac{ \mathrm{F}(k,\ell) \hskip.06cm \mathrm{F}(k+2,\ell)}{\mathrm{F}(k+1,\ell)^2} \ \geq \ \frac{1}{2n\ell^2 k}\hskip.06cm. \end{align*} $$
Proof First, observe that
![]() $b(z_1,z_2)\leq k+1$
and
$b(z_1,z_2)\leq k+1$
and
![]() $t(z_1) + t^*(z_2) \leq b(z_1)+b^*(z_2) \leq n$
. We then have
$t(z_1) + t^*(z_2) \leq b(z_1)+b^*(z_2) \leq n$
. We then have
 $$ \begin{align} \nonumber & \min\{b(z_1,z_2)-1,t(z_2)\}\hskip.03cm \big(\min\{\ell-1,t(z_3)\} \hskip.06cm + \hskip.06cm \min\{\ell-1,t^*(z_1)-1\}\big)\\ & \qquad + \, \min\{ k, t^*(z_1)\} \, +\, \min\{k, t(z_3)-1\} \ \leq \ k (2\ell-2) + 2k \ = \ 2k\ell \end{align} $$
$$ \begin{align} \nonumber & \min\{b(z_1,z_2)-1,t(z_2)\}\hskip.03cm \big(\min\{\ell-1,t(z_3)\} \hskip.06cm + \hskip.06cm \min\{\ell-1,t^*(z_1)-1\}\big)\\ & \qquad + \, \min\{ k, t^*(z_1)\} \, +\, \min\{k, t(z_3)-1\} \ \leq \ k (2\ell-2) + 2k \ = \ 2k\ell \end{align} $$
and
 $$ \begin{align*}\frac{ \textrm{F}(k,\ell) \hskip.06cm \textrm{F}(k+2,\ell)}{\textrm{F}(k+1,\ell)^2} \ \geq \ \left(\frac{1}{n\ell}\right) \cdot \left(\frac{1}{2k\ell}\right), \end{align*} $$
$$ \begin{align*}\frac{ \textrm{F}(k,\ell) \hskip.06cm \textrm{F}(k+2,\ell)}{\textrm{F}(k+1,\ell)^2} \ \geq \ \left(\frac{1}{n\ell}\right) \cdot \left(\frac{1}{2k\ell}\right), \end{align*} $$
as desired.
We also need the following variation on this proposition.
Proposition 6.4 Let
![]() $P=(X,\prec )$
be either a t-thin or t-flat poset with respect to
$P=(X,\prec )$
be either a t-thin or t-flat poset with respect to
![]() $\{z_1,z_2,z_3\}$
. Suppose also that
$\{z_1,z_2,z_3\}$
. Suppose also that
![]() $\textrm {F}(k,\ell ) \hskip .06cm \textrm {F}(k+2,\ell )> 0$
. Then we have
$\textrm {F}(k,\ell ) \hskip .06cm \textrm {F}(k+2,\ell )> 0$
. Then we have
 $$ \begin{align*} \frac{\mathrm{F}(k,\ell)\mathrm{F}(k+2,\ell)}{ \mathrm{F}(k+1,\ell)^2 } \ \geq \ \max \left\{\hskip.03cm\frac{1}{2k\ell(\ell+1)t} \ , \, \frac{1}{2t(t+1)^3} \hskip.03cm \right\}. \end{align*} $$
$$ \begin{align*} \frac{\mathrm{F}(k,\ell)\mathrm{F}(k+2,\ell)}{ \mathrm{F}(k+1,\ell)^2 } \ \geq \ \max \left\{\hskip.03cm\frac{1}{2k\ell(\ell+1)t} \ , \, \frac{1}{2t(t+1)^3} \hskip.03cm \right\}. \end{align*} $$
Proof We follow the proof of the proposition above with the following adjustments. For the first inequality in the maximum, we replace the bound (6.2) with the following:
Now the first inequality follows from Lemmas 6.1 and 6.2, with the parameters bounded by (6.1) and (6.3).
For the second inequality in the maximum, we replace the bounds (6.1) and (6.2) with the following:
 $$ \begin{align} \nonumber & \min\{b(z_1,z_2)-1,t(z_2)\}\hskip.03cm \big(\min\{\ell-1,t(z_3)\} \hskip.06cm + \hskip.06cm \min\{\ell-1,t^*(z_1)-1\}\big)\\ & \qquad + \, \min\{ k, t^*(z_1)\} \, +\, \min\{k, t(z_3)-1\} \ \leq \ t(2t-1) + t + (t-1) \, < \, 2t(t+1) \end{align} $$
$$ \begin{align} \nonumber & \min\{b(z_1,z_2)-1,t(z_2)\}\hskip.03cm \big(\min\{\ell-1,t(z_3)\} \hskip.06cm + \hskip.06cm \min\{\ell-1,t^*(z_1)-1\}\big)\\ & \qquad + \, \min\{ k, t^*(z_1)\} \, +\, \min\{k, t(z_3)-1\} \ \leq \ t(2t-1) + t + (t-1) \, < \, 2t(t+1) \end{align} $$
and
Now the second inequality follows from Lemmas 6.1 and 6.2, with the parameters bounded by (6.4) and (6.5).
Theorem 6.5 Suppose that
![]() $\textrm {F}(k+2,\ell )> 0$
and
$\textrm {F}(k+2,\ell )> 0$
and
![]() $\textrm {F}(k,\ell +2)=0$
. Then we have
$\textrm {F}(k,\ell +2)=0$
. Then we have
Proof We can assume that
![]() ${\textrm {F}(k,\ell )\hskip .06cm \textrm {F}(k+1,\ell +1)}>0$
as otherwise the result is trivial. Propositions 3.4 and 6.3 then give
${\textrm {F}(k,\ell )\hskip .06cm \textrm {F}(k+1,\ell +1)}>0$
as otherwise the result is trivial. Propositions 3.4 and 6.3 then give
 $$ \begin{align*} \frac{ \textrm{F}(k+1,\ell)\textrm{F}(k,\ell+1) }{\textrm{F}(k+1,\ell+1)\textrm{F}(k,\ell)} \ \geq \ \bigg(1 + \sqrt{1 - \frac{1}{2nk\ell^2} } \hskip.06cm\bigg)^{-1} \ \geq \ \frac12 \, + \, \frac{1}{16nk\ell^2}\,, \end{align*} $$
$$ \begin{align*} \frac{ \textrm{F}(k+1,\ell)\textrm{F}(k,\ell+1) }{\textrm{F}(k+1,\ell+1)\textrm{F}(k,\ell)} \ \geq \ \bigg(1 + \sqrt{1 - \frac{1}{2nk\ell^2} } \hskip.06cm\bigg)^{-1} \ \geq \ \frac12 \, + \, \frac{1}{16nk\ell^2}\,, \end{align*} $$
where the last inequality follows from
![]() $\frac 1{1+\sqrt {1-\alpha }} \ge \frac {1}{2}+ \frac {\alpha }{8}$
for
$\frac 1{1+\sqrt {1-\alpha }} \ge \frac {1}{2}+ \frac {\alpha }{8}$
for
![]() $0\le \alpha < 1$
.
$0\le \alpha < 1$
.
Theorem 6.6 Let
![]() $P=(X,\prec )$
be either a t-thin or t-flat poset with respect to
$P=(X,\prec )$
be either a t-thin or t-flat poset with respect to
![]() $\{z_1,z_2,z_3\}$
. Suppose also that
$\{z_1,z_2,z_3\}$
. Suppose also that
![]() $\textrm {F}(k,\ell +2)=0$
and
$\textrm {F}(k,\ell +2)=0$
and
![]() $\textrm {F}(k+2,\ell )> 0$
. Then we have
$\textrm {F}(k+2,\ell )> 0$
. Then we have
 $$ \begin{align*}{\mathrm{F}(k+1,\ell) \hskip.06cm \mathrm{F}(k,\ell+1)} \ \geq \ {\mathrm{F}(k,\ell) \hskip.06cm \mathrm{F}(k+1,\ell+1)} \hskip.06cm \max \left\{\frac12 \hskip.06cm + \hskip.06cm \frac{1}{16k\ell (\ell+1)t} \ ,\,\frac12 \hskip.06cm + \hskip.06cm \frac{1}{16t(t+1)^3} \right\}.\end{align*} $$
$$ \begin{align*}{\mathrm{F}(k+1,\ell) \hskip.06cm \mathrm{F}(k,\ell+1)} \ \geq \ {\mathrm{F}(k,\ell) \hskip.06cm \mathrm{F}(k+1,\ell+1)} \hskip.06cm \max \left\{\frac12 \hskip.06cm + \hskip.06cm \frac{1}{16k\ell (\ell+1)t} \ ,\,\frac12 \hskip.06cm + \hskip.06cm \frac{1}{16t(t+1)^3} \right\}.\end{align*} $$
6.3 Putting everything together
We can now combine the results to finish the proofs.
Proof of Main Theorem 1.2
The first inequality (1.1) follows immediately from Theorem 5.6. The second inequality (1.2) follows immediately from Theorem 6.5. The third inequality (1.3) follows by the symmetry
![]() $P \leftrightarrow P^\ast $
,
$P \leftrightarrow P^\ast $
,
![]() $z_1 \leftrightarrow z_3$
and
$z_1 \leftrightarrow z_3$
and
![]() $k\leftrightarrow \ell $
. Finally, the equality (1.4) is the equality in Lemma 4.4.
$k\leftrightarrow \ell $
. Finally, the equality (1.4) is the equality in Lemma 4.4.
Proof of Theorem 1.3
The proof of (1.5) follows the previous proof. The result is trivial in the case
![]() $\textrm {F}(k,\ell ) \hskip .06cm \textrm {F}(k+1,\ell +1) = 0$
. In the vanishing case
$\textrm {F}(k,\ell ) \hskip .06cm \textrm {F}(k+1,\ell +1) = 0$
. In the vanishing case
![]() $\textrm {F}(k,\ell +2) = \textrm {F}(k+2,\ell )=0$
and
$\textrm {F}(k,\ell +2) = \textrm {F}(k+2,\ell )=0$
and
![]() $\textrm {F}(k,\ell ) \hskip .06cm \textrm {F}(k+1,\ell +1)> 0$
, the result follows from the equality in Lemma 4.4. In the case when only one of the terms is vanishing:
$\textrm {F}(k,\ell ) \hskip .06cm \textrm {F}(k+1,\ell +1)> 0$
, the result follows from the equality in Lemma 4.4. In the case when only one of the terms is vanishing:
![]() $\textrm {F}(k,\ell +2)=0$
and
$\textrm {F}(k,\ell +2)=0$
and
![]() $\textrm {F}(k+2,\ell )> 0$
, the result is given by Theorem 6.6. The case
$\textrm {F}(k+2,\ell )> 0$
, the result is given by Theorem 6.6. The case
![]() $\textrm {F}(k+2,\ell )=0$
and
$\textrm {F}(k+2,\ell )=0$
and
![]() $\textrm {F}(k,\ell +2)> 0$
follows via poset duality as in the proof above. Finally, the nonvanishing case
$\textrm {F}(k,\ell +2)> 0$
follows via poset duality as in the proof above. Finally, the nonvanishing case
![]() $\textrm {F}(k,\ell +2)=\textrm {F}(k+2,\ell )>0$
is given by the second inequality in Theorem 5.5.
$\textrm {F}(k,\ell +2)=\textrm {F}(k+2,\ell )>0$
is given by the second inequality in Theorem 5.5.
Proof of Theorem 1.4
Lemma 6.1, combined with (6.1), gives
 $$ \begin{align*}\frac{\textrm{F}(k+1,\ell)}{\textrm{F}(k,\ell) } \, \leq \, 2k\ell.\end{align*} $$
$$ \begin{align*}\frac{\textrm{F}(k+1,\ell)}{\textrm{F}(k,\ell) } \, \leq \, 2k\ell.\end{align*} $$
Similarly, Lemma 6.2 for
![]() $k'=k-1$
and
$k'=k-1$
and
![]() $\ell '=\ell +1$
, combined with (6.2), gives
$\ell '=\ell +1$
, combined with (6.2), gives
 $$ \begin{align*}\frac{\textrm{F}(k,\ell+1)}{\textrm{F}(k+1,\ell+1)} \, = \, \frac{\textrm{F}(k'+1,\ell')}{\textrm{F}(k'+2,\ell')} \, \leq \, n \ell' \, = \, n(\ell+1). \end{align*} $$
$$ \begin{align*}\frac{\textrm{F}(k,\ell+1)}{\textrm{F}(k+1,\ell+1)} \, = \, \frac{\textrm{F}(k'+1,\ell')}{\textrm{F}(k'+2,\ell')} \, \leq \, n \ell' \, = \, n(\ell+1). \end{align*} $$
Multiplying these inequalities, we obtain the first term in the minimum of the desired upper bound. Via poset duality (see the proof of Theorem 1.2 above), we can exchange the k and
![]() $\ell $
terms and obtain the other inequality.
$\ell $
terms and obtain the other inequality.
7 Examples and counterexamples
7.1 Inequalities (CPC1) and (CPC2)
Recall that by Theorem 1.7 at least one of these two inequalities must hold. We now show that for some posets (CPC2) does not hold. By the poset duality, the inequality (CPC1) also does not hold.
Proposition 7.1 The inequality (CPC2) fails for an infinite family of posets of width 3.
Proof Fix
![]() $k \geq 1$
and
$k \geq 1$
and
![]() $\ell \geq 2$
, and let
$\ell \geq 2$
, and let
![]() $P:=(X,\prec )$
be the poset given by
$P:=(X,\prec )$
be the poset given by
 $$ \begin{align*} & X \ := \ \{x_1,\ldots, x_{k-1}\} \ \sqcup \ \{y_1,\ldots, y_{\ell-2}\} \ \sqcup \ \{z_1, z_2, z_3 \} \ \ \sqcup \ \ \{u,v,w\}\hskip.06cm, \\ & z_1 \hskip.06cm \prec \hskip.06cm x_1 \hskip.06cm \prec \hskip.06cm x_2 \hskip.06cm \prec \hskip.06cm \cdots \hskip.06cm \prec \hskip.06cm x_{k-1} \hskip.06cm \prec \hskip.06cm z_2 \hskip.06cm \prec \hskip.06cm y_1 \hskip.06cm \prec \hskip.06cm y_2 \hskip.06cm \prec \hskip.06cm \cdots \hskip.06cm \prec \hskip.06cm y_{\ell-2} \hskip.06cm \prec \hskip.06cm z_3\hskip.06cm,\\ & x_{k-1} \hskip.06cm \prec u \hskip.06cm \prec \hskip.06cm y_1\hskip.06cm, \ \ v \hskip.06cm \succ \hskip.06cm z_2\hskip.06cm, \ \ w \hskip.06cm \succ \hskip.06cm z_2\hskip.06cm. \end{align*} $$
$$ \begin{align*} & X \ := \ \{x_1,\ldots, x_{k-1}\} \ \sqcup \ \{y_1,\ldots, y_{\ell-2}\} \ \sqcup \ \{z_1, z_2, z_3 \} \ \ \sqcup \ \ \{u,v,w\}\hskip.06cm, \\ & z_1 \hskip.06cm \prec \hskip.06cm x_1 \hskip.06cm \prec \hskip.06cm x_2 \hskip.06cm \prec \hskip.06cm \cdots \hskip.06cm \prec \hskip.06cm x_{k-1} \hskip.06cm \prec \hskip.06cm z_2 \hskip.06cm \prec \hskip.06cm y_1 \hskip.06cm \prec \hskip.06cm y_2 \hskip.06cm \prec \hskip.06cm \cdots \hskip.06cm \prec \hskip.06cm y_{\ell-2} \hskip.06cm \prec \hskip.06cm z_3\hskip.06cm,\\ & x_{k-1} \hskip.06cm \prec u \hskip.06cm \prec \hskip.06cm y_1\hskip.06cm, \ \ v \hskip.06cm \succ \hskip.06cm z_2\hskip.06cm, \ \ w \hskip.06cm \succ \hskip.06cm z_2\hskip.06cm. \end{align*} $$
Note that this is a poset of width 3. Let us now compute all four terms in (CPC2):
First, observe that
![]() $L\in \mathcal F(k,\ell +2)$
if and only if
$L\in \mathcal F(k,\ell +2)$
if and only if
![]() $L(z_2) < L(u) < L(y_1)$
and
$L(z_2) < L(u) < L(y_1)$
and
![]() $L(v), L(w)<L(z_3)$
. Thus, there is a bijection between these linear extensions and the pairs
$L(v), L(w)<L(z_3)$
. Thus, there is a bijection between these linear extensions and the pairs
![]() $(i,j)$
satisfying
$(i,j)$
satisfying
![]() $1 \leq i \neq j \leq \ell +1$
, through the map
$1 \leq i \neq j \leq \ell +1$
, through the map
![]() $L \mapsto \big (L(v)-L(z_2), L(w)-L(z_2)\big )$
. Therefore, we have
$L \mapsto \big (L(v)-L(z_2), L(w)-L(z_2)\big )$
. Therefore, we have
![]() $\textrm {F}(k,\ell +2)=(\ell +1)\ell $
.
$\textrm {F}(k,\ell +2)=(\ell +1)\ell $
.
Second, observe that
![]() $L\in \mathcal F(k+1,\ell )$
if and only if
$L\in \mathcal F(k+1,\ell )$
if and only if
![]() $L(x_{k-1}) < L(u)<L(z_2) $
, and either
$L(x_{k-1}) < L(u)<L(z_2) $
, and either
![]() $L(v)< L(z_3) <L(w)$
or
$L(v)< L(z_3) <L(w)$
or
![]() $L(w)< L(z_3) <L(v)$
. Note that there is a bijection between those linear extensions satisfying
$L(w)< L(z_3) <L(v)$
. Note that there is a bijection between those linear extensions satisfying
![]() $L(v)< L(z_3) <L(w)$
and the integers in
$L(v)< L(z_3) <L(w)$
and the integers in
![]() $[1,\ell -1]$
, through the map
$[1,\ell -1]$
, through the map
![]() $L\mapsto L(v)-L(z_2)$
. Therefore, we have
$L\mapsto L(v)-L(z_2)$
. Therefore, we have
![]() $\textrm {F}(k+1,\ell )=2(\ell -1)$
.
$\textrm {F}(k+1,\ell )=2(\ell -1)$
.
Third, observe that
![]() $L\in \mathcal F(k,\ell +1)$
if and only if
$L\in \mathcal F(k,\ell +1)$
if and only if
![]() $L(z_2) < L(u) < L(y_1)$
, and either
$L(z_2) < L(u) < L(y_1)$
, and either
![]() $L(v)< L(z_3) <L(w)$
or
$L(v)< L(z_3) <L(w)$
or
![]() $L(w)< L(z_3) <L(v)$
. Note that there is a bijection between those linear extensions satisfying
$L(w)< L(z_3) <L(v)$
. Note that there is a bijection between those linear extensions satisfying
![]() $L(v)< L(z_3) <L(w)$
and the integers in
$L(v)< L(z_3) <L(w)$
and the integers in
![]() $[1,\ell ]$
, through the map
$[1,\ell ]$
, through the map
![]() $L\mapsto L(v)-L(z_2)$
. Therefore, we have
$L\mapsto L(v)-L(z_2)$
. Therefore, we have
![]() $\textrm {F}(k,\ell +1)=2\ell $
.
$\textrm {F}(k,\ell +1)=2\ell $
.
Fourth, observe that
![]() $L\in \mathcal F(k+1,\ell +1)$
if and only if
$L\in \mathcal F(k+1,\ell +1)$
if and only if
![]() $L(x_{k-1}) < L(u)<L(z_2)$
and
$L(x_{k-1}) < L(u)<L(z_2)$
and
![]() $L(v),L(w)<L(z_3)$
. Note that there is a bijection between these linear extensions and pairs
$L(v),L(w)<L(z_3)$
. Note that there is a bijection between these linear extensions and pairs
![]() $(i,j)$
satisfying
$(i,j)$
satisfying
![]() $1 \leq i \neq j \leq \ell $
. Therefore, we have
$1 \leq i \neq j \leq \ell $
. Therefore, we have
![]() $\textrm {F}(k+1,\ell +1)=\ell (\ell -1)$
.
$\textrm {F}(k+1,\ell +1)=\ell (\ell -1)$
.
Combining these observations, we obtain
 $$\begin{align*}\frac{\textrm{F}(k,\ell+1) \hskip.06cm \textrm{F}(k+1,\ell+1)}{\textrm{F}({k,\ell+2}) \hskip.06cm \textrm{F}(k+1,\ell)} \ = \ \frac{\ell}{\ell+1} \ < \ 1\hskip.03cm. \end{align*}$$
$$\begin{align*}\frac{\textrm{F}(k,\ell+1) \hskip.06cm \textrm{F}(k+1,\ell+1)}{\textrm{F}({k,\ell+2}) \hskip.06cm \textrm{F}(k+1,\ell)} \ = \ \frac{\ell}{\ell+1} \ < \ 1\hskip.03cm. \end{align*}$$
This contradicts (CPC2), as desired.
7.2 Counterexamples to the generalized CPC
We now show that the examples in proof of Proposition 7.2 are also counterexamples to Conjecture 1.5, thus proving Theorem 1.6.
Proof Suppose (CPC2) fails for a poset
![]() $P=(X,\prec )$
, elements
$P=(X,\prec )$
, elements
![]() $z_1, z_2, z_3\in X$
, and integers
$z_1, z_2, z_3\in X$
, and integers
![]() $k,\ell \ge 1$
.
$k,\ell \ge 1$
.
Let
![]() $z_1':=z_2$
,
$z_1':=z_2$
,
![]() $z_2':=z_1$
, and
$z_2':=z_1$
, and
![]() $z_3':=z_3$
. To avoid the clash of notation, let
$z_3':=z_3$
. To avoid the clash of notation, let
![]() $\textrm {F}'(k,\ell )$
be defined by
$\textrm {F}'(k,\ell )$
be defined by
By definition, we have
Now let
![]() $a:=-k-1$
and
$a:=-k-1$
and
![]() $b:=\ell +k+1$
. Note aside that
$b:=\ell +k+1$
. Note aside that
![]() $a<0$
for all
$a<0$
for all
![]() $k>0$
. It then follows that
$k>0$
. It then follows that
 $$ \begin{align*} \textrm{F}'(a,b) \ &= \ \textrm{F}(-a,a+b) \ = \ \textrm{F}(k+1,\ell), \\ \textrm{F}'(a+1,b+1) \ &= \ \textrm{F}(-a-1,a+b+2) \ = \ \textrm{F}(k,\ell+2), \\ \textrm{F}'(a,b+1) \ &= \ \textrm{F}(-a,a+b+1) \ = \ \textrm{F}(k+1,\ell+1), \\ \textrm{F}'(a+1,b) \ &= \ \textrm{F}(-a-1,a+b+1) \ = \ \textrm{F}(k,\ell+1). \end{align*} $$
$$ \begin{align*} \textrm{F}'(a,b) \ &= \ \textrm{F}(-a,a+b) \ = \ \textrm{F}(k+1,\ell), \\ \textrm{F}'(a+1,b+1) \ &= \ \textrm{F}(-a-1,a+b+2) \ = \ \textrm{F}(k,\ell+2), \\ \textrm{F}'(a,b+1) \ &= \ \textrm{F}(-a,a+b+1) \ = \ \textrm{F}(k+1,\ell+1), \\ \textrm{F}'(a+1,b) \ &= \ \textrm{F}(-a-1,a+b+1) \ = \ \textrm{F}(k,\ell+1). \end{align*} $$
In the new notation, the inequality (CPC2) is equivalent to
and note that
![]() $a<0$
,
$a<0$
,
![]() $b>0$
whenever
$b>0$
whenever
![]() $k,\ell>0$
. This shows that a counterexample for (CPC2) is also a counterexample to (GCPC).
$k,\ell>0$
. This shows that a counterexample for (CPC2) is also a counterexample to (GCPC).
This follows from Proposition 7.2 and Theorem 3.3 in [Reference Chan, Pak and PanovaCPP22] which proves (GCPC) for posets of width 2.
7.3 Stanley ratio
It follows from Corollary 5.2, the following bound on the Stanley ratio:
 $$ \begin{align} \frac{\textrm{N}_k^2}{\textrm{N}_{k-1}\hskip.06cm \textrm{N}_{k+1} } \ \leq \ {(k-1)(n-k)}, \end{align} $$
$$ \begin{align} \frac{\textrm{N}_k^2}{\textrm{N}_{k-1}\hskip.06cm \textrm{N}_{k+1} } \ \leq \ {(k-1)(n-k)}, \end{align} $$
whenever the LHS is well defined. The following example shows that both the inequality (7.1) and Corollary 5.2 are tight.
In the notation of Section 5.2, fix
![]() $1\le k \le n$
. Let
$1\le k \le n$
. Let
![]() $P_k:=(X,\prec )$
be the width 2 poset given by
$P_k:=(X,\prec )$
be the width 2 poset given by
 $$ \begin{align*} & X \ := \ \{x_1,\ldots, x_{k-2}\} \ \sqcup \ \{y_1,\ldots, y_{n-k-1}\} \ \sqcup \ \{a, v, w \}, \\ & x_1 \hskip.06cm \prec \hskip.06cm x_2 \hskip.06cm \prec \hskip.06cm \cdots \hskip.06cm \prec \hskip.06cm x_{k-2} \hskip.06cm \prec \hskip.06cm a \hskip.06cm \prec \hskip.06cm y_1 \hskip.06cm \prec \hskip.06cm y_2 \hskip.06cm \prec \hskip.06cm \cdots \hskip.06cm \prec \hskip.06cm y_{n-k-1},\\ & v \hskip.06cm \prec \hskip.06cm y_1\hskip.03cm, \ \ w \hskip.06cm \succ \hskip.06cm x_1\hskip.03cm, \ \ v \hskip.06cm \prec \hskip.06cm w. \end{align*} $$
$$ \begin{align*} & X \ := \ \{x_1,\ldots, x_{k-2}\} \ \sqcup \ \{y_1,\ldots, y_{n-k-1}\} \ \sqcup \ \{a, v, w \}, \\ & x_1 \hskip.06cm \prec \hskip.06cm x_2 \hskip.06cm \prec \hskip.06cm \cdots \hskip.06cm \prec \hskip.06cm x_{k-2} \hskip.06cm \prec \hskip.06cm a \hskip.06cm \prec \hskip.06cm y_1 \hskip.06cm \prec \hskip.06cm y_2 \hskip.06cm \prec \hskip.06cm \cdots \hskip.06cm \prec \hskip.06cm y_{n-k-1},\\ & v \hskip.06cm \prec \hskip.06cm y_1\hskip.03cm, \ \ w \hskip.06cm \succ \hskip.06cm x_1\hskip.03cm, \ \ v \hskip.06cm \prec \hskip.06cm w. \end{align*} $$
Proposition 7.4 For posets
![]() $P_k$
defined above, the inequality (7.1) is an equality.
$P_k$
defined above, the inequality (7.1) is an equality.
Proof Note that for all linear extensions
![]() $L \in \mathcal {N}_{k-1}$
, we have
$L \in \mathcal {N}_{k-1}$
, we have
![]() $L(a) < L(v)=k < L(w)$
, where
$L(a) < L(v)=k < L(w)$
, where
![]() $k+1 \le L(w) \le n$
. Similarly, for all linear extensions
$k+1 \le L(w) \le n$
. Similarly, for all linear extensions
![]() $L \in \mathcal {N}_{k}$
, we have
$L \in \mathcal {N}_{k}$
, we have
![]() $L(v) <L(a) < L(w)$
, where
$L(v) <L(a) < L(w)$
, where
![]() $1 \le L(v) \le k-1$
and
$1 \le L(v) \le k-1$
and
![]() $k+1\le L(w) \le n$
. Finally, for all linear extensions
$k+1\le L(w) \le n$
. Finally, for all linear extensions
![]() $L \in \mathcal {N}_{k+1}$
, we have
$L \in \mathcal {N}_{k+1}$
, we have
![]() $L(v)< L(w)=k < L(a)$
, where
$L(v)< L(w)=k < L(a)$
, where
![]() $1 \le L(v) \le k-1$
. These three observation imply that
$1 \le L(v) \le k-1$
. These three observation imply that
Thus, for posets
![]() $P_k$
, the inequality (7.1) is an equality.
$P_k$
, the inequality (7.1) is an equality.
7.4 Converse cross-product ratio
The following example shows that Theorem 1.4 is essentially tight, up to a multiplicative factor of
![]() $2\ell $
. Fix
$2\ell $
. Fix
![]() $k \geq 2$
,
$k \geq 2$
,
![]() $\ell \geq 1$
, and denote
$\ell \geq 1$
, and denote
![]() $m:=n-k-\ell -3$
. Let
$m:=n-k-\ell -3$
. Let
![]() $P_{k,\ell }:=(X,\prec )$
be the poset given by
$P_{k,\ell }:=(X,\prec )$
be the poset given by
 $$ \begin{align*} & X \ := \ \{a_1,\ldots, a_{k-2}\} \ \sqcup \ \{b_1,\ldots, b_{\ell-1}\} \ \sqcup \ \{c_1,\ldots, c_{m}\} \ \sqcup \ \{z_1, z_2, z_3 \} \ \sqcup \ \{u,v,w\}, \\ & z_1 \hskip.06cm \prec \hskip.06cm a_1 \hskip.06cm \prec \hskip.06cm \cdots \hskip.06cm \prec \hskip.06cm a_{k-2} \hskip.06cm \prec \hskip.06cm z_2 \hskip.06cm \prec \hskip.06cm b_1 \hskip.06cm \prec \hskip.06cm \cdots \hskip.06cm \prec \hskip.06cm b_{\ell-1} \hskip.06cm \prec \hskip.06cm z_3 \hskip.06cm \prec \hskip.06cm c_1 \hskip.06cm \prec \hskip.06cm \cdots \hskip.06cm \prec \hskip.06cm c_m,\\ & u \hskip.06cm \prec \hskip.06cm z_2\hskip.03cm, \ \ a_{k-2} \hskip.06cm \prec \hskip.06cm v \hskip.06cm \prec \hskip.06cm z_3\hskip.03cm, \ \ w \hskip.06cm \succ \hskip.06cm b_{\ell-1}\hskip.03cm, \ \ u \hskip.06cm \prec v \hskip.06cm \prec \hskip.06cm w. \end{align*} $$
$$ \begin{align*} & X \ := \ \{a_1,\ldots, a_{k-2}\} \ \sqcup \ \{b_1,\ldots, b_{\ell-1}\} \ \sqcup \ \{c_1,\ldots, c_{m}\} \ \sqcup \ \{z_1, z_2, z_3 \} \ \sqcup \ \{u,v,w\}, \\ & z_1 \hskip.06cm \prec \hskip.06cm a_1 \hskip.06cm \prec \hskip.06cm \cdots \hskip.06cm \prec \hskip.06cm a_{k-2} \hskip.06cm \prec \hskip.06cm z_2 \hskip.06cm \prec \hskip.06cm b_1 \hskip.06cm \prec \hskip.06cm \cdots \hskip.06cm \prec \hskip.06cm b_{\ell-1} \hskip.06cm \prec \hskip.06cm z_3 \hskip.06cm \prec \hskip.06cm c_1 \hskip.06cm \prec \hskip.06cm \cdots \hskip.06cm \prec \hskip.06cm c_m,\\ & u \hskip.06cm \prec \hskip.06cm z_2\hskip.03cm, \ \ a_{k-2} \hskip.06cm \prec \hskip.06cm v \hskip.06cm \prec \hskip.06cm z_3\hskip.03cm, \ \ w \hskip.06cm \succ \hskip.06cm b_{\ell-1}\hskip.03cm, \ \ u \hskip.06cm \prec v \hskip.06cm \prec \hskip.06cm w. \end{align*} $$
Proposition 7.5 Fix
![]() $k \geq 2$
,
$k \geq 2$
,
![]() $\ell \geq 1$
. For posets
$\ell \geq 1$
. For posets
![]() $P_{k,\ell }$
defined above, we have
$P_{k,\ell }$
defined above, we have
 $$ \begin{align} \frac{\mathrm{F}(k,\ell+1) \hskip.06cm \mathrm{F}(k+1,\ell)}{\mathrm{F}(k,\ell) \hskip.06cm \mathrm{F}(k+1,\ell+1)} \ = \ k\ell n \big(1+o(1)\big) \ \ \text{as} \ n\to \infty. \end{align} $$
$$ \begin{align} \frac{\mathrm{F}(k,\ell+1) \hskip.06cm \mathrm{F}(k+1,\ell)}{\mathrm{F}(k,\ell) \hskip.06cm \mathrm{F}(k+1,\ell+1)} \ = \ k\ell n \big(1+o(1)\big) \ \ \text{as} \ n\to \infty. \end{align} $$
Proof Note that for every linear extension
![]() $L\in \mathcal {E}(P_{k,\ell })$
, we have
$L\in \mathcal {E}(P_{k,\ell })$
, we have
Note also that
We now compute the cross-product ratio of
![]() $P_{k,\ell }$
and consider the following four cases.
$P_{k,\ell }$
and consider the following four cases.
Case 1. Let
![]() $L \in \mathcal F(k,\ell )$
. Since
$L \in \mathcal F(k,\ell )$
. Since
![]() $L(z_3)-L(z_2)=\ell $
, it then follows from (7.4) that both
$L(z_3)-L(z_2)=\ell $
, it then follows from (7.4) that both
![]() $L(v)$
and
$L(v)$
and
![]() $L(w)$
are not contained in the interval
$L(w)$
are not contained in the interval
![]() $[L(z_2),L(z_3)]$
. It then follows from (7.6) and (7.7) that
$[L(z_2),L(z_3)]$
. It then follows from (7.6) and (7.7) that
![]() $L(v)= L(z_2)-1$
and
$L(v)= L(z_2)-1$
and
![]() $L(w)>L(z_3)$
, respectively. Now, since
$L(w)>L(z_3)$
, respectively. Now, since
![]() $L(z_2)-L(z_1)=k$
and
$L(z_2)-L(z_1)=k$
and
![]() $L(v)\in \big [L(z_1),L(z_2)\big ]$
, it then follows from (7.3) that
$L(v)\in \big [L(z_1),L(z_2)\big ]$
, it then follows from (7.3) that
![]() $L(u)$
is not contained in the interval
$L(u)$
is not contained in the interval
![]() $[L(z_1),L(z_2)]$
. It then follows from (7.5) that
$[L(z_1),L(z_2)]$
. It then follows from (7.5) that
![]() $L(u)=1$
, which in turn implies that
$L(u)=1$
, which in turn implies that
![]() $L(z_1)=2$
. We conclude that
$L(z_1)=2$
. We conclude that
![]() $L \in \mathcal F(k,\ell )$
satisfy
$L \in \mathcal F(k,\ell )$
satisfy
 $$\begin{align*}\begin{aligned}{3} &L(z_1)=2, \quad && L(z_2)=k+2, \quad &&L(z_3)=k+\ell+2, \\ & L(u)=1, \quad && L(v)=k+1, \quad && L(w) \in [k+\ell+3,n]. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned}{3} &L(z_1)=2, \quad && L(z_2)=k+2, \quad &&L(z_3)=k+\ell+2, \\ & L(u)=1, \quad && L(v)=k+1, \quad && L(w) \in [k+\ell+3,n]. \end{aligned} \end{align*}$$
This implies that
![]() $\textrm {F}(k,\ell )=n-k-\ell -2$
, as desired.
$\textrm {F}(k,\ell )=n-k-\ell -2$
, as desired.
Case 2. Let
![]() $L \in \mathcal F(k+1,\ell )$
. Since
$L \in \mathcal F(k+1,\ell )$
. Since
![]() $L(z_3)-L(z_2)=\ell $
, it then follows from (7.4) that both
$L(z_3)-L(z_2)=\ell $
, it then follows from (7.4) that both
![]() $L(v)$
and
$L(v)$
and
![]() $L(w)$
are not contained in the interval
$L(w)$
are not contained in the interval
![]() $[L(z_2),L(z_3)]$
. It then follows from (7.6) and (7.7) that
$[L(z_2),L(z_3)]$
. It then follows from (7.6) and (7.7) that
![]() $L(v)= L(z_2)-1$
and
$L(v)= L(z_2)-1$
and
![]() $L(w)>L(z_3)$
, respectively. Now, since
$L(w)>L(z_3)$
, respectively. Now, since
![]() $L(z_2)-L(z_1)=k+1$
and
$L(z_2)-L(z_1)=k+1$
and
![]() $L(v)\in \big [L(z_1),L(z_2)\big ]$
, it then follows from (7.3) that
$L(v)\in \big [L(z_1),L(z_2)\big ]$
, it then follows from (7.3) that
![]() $L(u)$
is contained in the interval
$L(u)$
is contained in the interval
![]() $[L(z_1),L(z_2)]$
. It then follows that
$[L(z_1),L(z_2)]$
. It then follows that
![]() $L(z_1)=1$
. We conclude that
$L(z_1)=1$
. We conclude that
![]() $L \in \mathcal F(k+1,\ell )$
satisfy
$L \in \mathcal F(k+1,\ell )$
satisfy
 $$\begin{align*}\begin{aligned}{3} &L(z_1)=1, \quad && L(z_2)=k+2, \quad &&L(z_3)=k+\ell+2, \\ & L(u)\in [2,k], \quad && L(v)=k+1, \quad && L(w) \in [k+\ell+3,n]. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned}{3} &L(z_1)=1, \quad && L(z_2)=k+2, \quad &&L(z_3)=k+\ell+2, \\ & L(u)\in [2,k], \quad && L(v)=k+1, \quad && L(w) \in [k+\ell+3,n]. \end{aligned} \end{align*}$$
This implies that
![]() $\textrm {F}(k+1,\ell )=(k-1)(n-k-\ell -2)$
.
$\textrm {F}(k+1,\ell )=(k-1)(n-k-\ell -2)$
.
Case 3. We have
![]() $\textrm {F}(k,\ell +1)=1+ (k-1) \, \ell (n-k-\ell -2)$
by the following argument. Let
$\textrm {F}(k,\ell +1)=1+ (k-1) \, \ell (n-k-\ell -2)$
by the following argument. Let
![]() $L \in \mathcal F(k,\ell +1)$
. By (7.5) either
$L \in \mathcal F(k,\ell +1)$
. By (7.5) either
![]() $L(u)=1$
or
$L(u)=1$
or
![]() $L(u) \in [L(z_1), L(z_2)]$
.
$L(u) \in [L(z_1), L(z_2)]$
.
Case 3.1. Assume that
![]() $L(u)=1$
. This implies that
$L(u)=1$
. This implies that
![]() $L(z_1)=2$
. Since
$L(z_1)=2$
. Since
![]() $L(u) \notin [L(z_1),L(z_2)]$
, it then follows from
$L(u) \notin [L(z_1),L(z_2)]$
, it then follows from
![]() $L(z_2)-L(z_1)=k$
and (7.3) that
$L(z_2)-L(z_1)=k$
and (7.3) that
![]() $L(v)$
is contained in the interval
$L(v)$
is contained in the interval
![]() $[L(z_1), L(z_2)]$
. It then follows from (7.6) that
$[L(z_1), L(z_2)]$
. It then follows from (7.6) that
![]() $L(v)=L(z_2)-1$
. Since
$L(v)=L(z_2)-1$
. Since
![]() $L(z_3)-L(z_2)=\ell +1$
and
$L(z_3)-L(z_2)=\ell +1$
and
![]() $L(v)\notin [L(z_2),L(z_3)]$
, it then follows from (7.4) that
$L(v)\notin [L(z_2),L(z_3)]$
, it then follows from (7.4) that
![]() $L(w)$
is contained in the interval
$L(w)$
is contained in the interval
![]() $[L(z_2),L(z_3)]$
. By (7.7), this implies that
$[L(z_2),L(z_3)]$
. By (7.7), this implies that
![]() $L(w)=L(z_3)-1$
. We conclude
$L(w)=L(z_3)-1$
. We conclude
 $$\begin{align*}\begin{aligned}{3} &L(z_1)=2, \quad && L(z_2)=k+2, \quad &&L(z_3)=k+\ell+3, \\ & L(u)=1, \quad && L(v)=k+1, \quad && L(w) =k+\ell+2. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned}{3} &L(z_1)=2, \quad && L(z_2)=k+2, \quad &&L(z_3)=k+\ell+3, \\ & L(u)=1, \quad && L(v)=k+1, \quad && L(w) =k+\ell+2. \end{aligned} \end{align*}$$
Thus, there is exactly one such linear extension.
Case 3.2. Assume that
![]() $L(u) \in [L(z_1), L(z_2)]$
. This implies that
$L(u) \in [L(z_1), L(z_2)]$
. This implies that
![]() $L(z_1)=1$
. Since
$L(z_1)=1$
. Since
![]() $L(z_2)-L(z_1)=k$
and
$L(z_2)-L(z_1)=k$
and
![]() $L(u) \in [L(z_1), L(z_2)]$
, it then follows from (7.3) that
$L(u) \in [L(z_1), L(z_2)]$
, it then follows from (7.3) that
![]() $L(v)$
is not contained in the interval
$L(v)$
is not contained in the interval
![]() $[L(z_1), L(z_2)]$
. By (7.6), this implies that
$[L(z_1), L(z_2)]$
. By (7.6), this implies that
![]() $L(v)$
is contained in the interval
$L(v)$
is contained in the interval
![]() $[L(z_2), L(z_3)]$
. Since
$[L(z_2), L(z_3)]$
. Since
![]() $L(z_3)-L(z_2)=\ell +1$
, it then follows from (7.4) that
$L(z_3)-L(z_2)=\ell +1$
, it then follows from (7.4) that
![]() $L(w)$
is not contained in the interval
$L(w)$
is not contained in the interval
![]() $[L(z_2), L(z_3)]$
. By (7.7), this implies that
$[L(z_2), L(z_3)]$
. By (7.7), this implies that
![]() $L(w)>L(z_3)$
. We conclude
$L(w)>L(z_3)$
. We conclude
 $$\begin{align*}\begin{aligned}{3} &L(z_1)=1, \quad && L(z_2)=k+1, \quad &&L(z_3)=k+\ell+2, \\ & L(u)\in[2,k], \quad && L(v)\in [k+2,k+\ell+1], \quad && L(w) \in [k+\ell+3,n]. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned}{3} &L(z_1)=1, \quad && L(z_2)=k+1, \quad &&L(z_3)=k+\ell+2, \\ & L(u)\in[2,k], \quad && L(v)\in [k+2,k+\ell+1], \quad && L(w) \in [k+\ell+3,n]. \end{aligned} \end{align*}$$
Thus, there are exactly
![]() $(k-1)\ell (n-k-\ell -2)$
such linear extensions.
$(k-1)\ell (n-k-\ell -2)$
such linear extensions.
Case 4. Let
![]() $L \in \mathcal F(k+1,\ell +1)$
. Since
$L \in \mathcal F(k+1,\ell +1)$
. Since
![]() $L(z_2)-L(z_1)=k+1$
, it follows from (7.3) that both
$L(z_2)-L(z_1)=k+1$
, it follows from (7.3) that both
![]() $L(u)$
and
$L(u)$
and
![]() $L(v)$
are contained in the interval
$L(v)$
are contained in the interval
![]() $[L(z_1),L(z_2)]$
. This implies that
$[L(z_1),L(z_2)]$
. This implies that
![]() $L(z_1)=1$
. Since
$L(z_1)=1$
. Since
![]() $L(v) \in [L(z_1),L(z_2)]$
, it then follows from (7.6) that
$L(v) \in [L(z_1),L(z_2)]$
, it then follows from (7.6) that
![]() $L(v)=L(z_2)-1$
. Now, since
$L(v)=L(z_2)-1$
. Now, since
![]() $L(z_3)-L(z_2)=\ell +1$
and
$L(z_3)-L(z_2)=\ell +1$
and
![]() $L(v) \notin [L(z_2), L(z_3)]$
, it then follows from (7.4) that
$L(v) \notin [L(z_2), L(z_3)]$
, it then follows from (7.4) that
![]() $L(w)$
is contained in the interval
$L(w)$
is contained in the interval
![]() $[L(z_2), L(z_3)]$
. By (7.7), this implies that
$[L(z_2), L(z_3)]$
. By (7.7), this implies that
![]() $L(w)=L(z_3)-1$
. We conclude that
$L(w)=L(z_3)-1$
. We conclude that
![]() $L \in \mathcal F(k+1,\ell +1)$
satisfy
$L \in \mathcal F(k+1,\ell +1)$
satisfy
 $$\begin{align*}\begin{aligned}{3} &L(z_1)=1, \quad && L(z_2)=k+2, \quad &&L(z_3)=k+\ell+3, \\ & L(u)\in [2,k], \quad && L(v)=k+1, \quad && L(w)=k+\ell+2. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned}{3} &L(z_1)=1, \quad && L(z_2)=k+2, \quad &&L(z_3)=k+\ell+3, \\ & L(u)\in [2,k], \quad && L(v)=k+1, \quad && L(w)=k+\ell+2. \end{aligned} \end{align*}$$
This implies that
![]() $\textrm {F}(k+1,\ell +1)=k-1$
.
$\textrm {F}(k+1,\ell +1)=k-1$
.
In summary, for the poset
![]() $P_{k,\ell }$
, we have
$P_{k,\ell }$
, we have
 $$\begin{align*}\frac{\textrm{F}(k,\ell+1) \hskip.06cm \textrm{F}(k+1,\ell)}{\textrm{F}(k,\ell) \hskip.06cm \textrm{F}(k+1,\ell+1)} \ = \ 1+ (k-1) \ell (n-k-\ell-2) \ = \ k\ell n \big(1+o(1)\big) \ \ \text{as} \ n\to \infty, \end{align*}$$
$$\begin{align*}\frac{\textrm{F}(k,\ell+1) \hskip.06cm \textrm{F}(k+1,\ell)}{\textrm{F}(k,\ell) \hskip.06cm \textrm{F}(k+1,\ell+1)} \ = \ 1+ (k-1) \ell (n-k-\ell-2) \ = \ k\ell n \big(1+o(1)\big) \ \ \text{as} \ n\to \infty, \end{align*}$$
as desired.
8 Final remarks
8.1
The CPP (Conjecture 1.1) has been a major open problem in the area for the past three decades, albeit with relatively little progress to show for i (see [Reference Chan and PakCP23b] for the background). The following quote about a closely related problem seems applicable:
“As sometimes happens, we cannot point to written evidence that the problem has received much attention; we can only say that a number of conversations over the last 10 years suggest that the absence of progress on the problem was not due to absence of effort.” [Reference Kahn and YangKY98, p. 87]
8.2
Theorem 2.4 is well known in the area and can be traced back to the works of Jean Favard in the early 1930s.Footnote 4 Of course, this is not the only Favard’s inequality known in the literature. In fact, Theorem 2.3, which goes back to [Reference MatsumuraMS32, Reference FenchelFW36], seem to also have been inspired by Favard’s work.Footnote 5 In a closely related context of Lorentzian polynomials, Favard’s inequality appears in [Reference Brändén and HuhBH20, Proposition 2.17]. For more on Theorem 2.3, see [Reference Bonnesen and FenchelBF87, Section 51] and the references therein.
8.3
As we mentioned in the introduction, the
![]() $\Upsilon \ge \frac 12$
lower bound derived from Favard’s inequality (Theorem 2.4) easily implies the
$\Upsilon \ge \frac 12$
lower bound derived from Favard’s inequality (Theorem 2.4) easily implies the
![]() $\hskip .03cm \frac 12 \hskip .03cm$
lower bound on the cross-product. Given the straightforward nature of this implication, one can think of this paper as the first attempt to finding the best
$\hskip .03cm \frac 12 \hskip .03cm$
lower bound on the cross-product. Given the straightforward nature of this implication, one can think of this paper as the first attempt to finding the best
![]() $\varepsilon \ge 0$
, such that
$\varepsilon \ge 0$
, such that
 $$ \begin{align*}\frac{\textrm{F}(k+1,\ell) \hskip.06cm \textrm{F}(k,\ell+1)}{\textrm{F}(k,\ell)\hskip.06cm \textrm{F}(k+1,\ell+1)} \, - \, \frac{1}{2} \ \geq \, \varepsilon. \end{align*} $$
$$ \begin{align*}\frac{\textrm{F}(k+1,\ell) \hskip.06cm \textrm{F}(k,\ell+1)}{\textrm{F}(k,\ell)\hskip.06cm \textrm{F}(k+1,\ell+1)} \, - \, \frac{1}{2} \ \geq \, \varepsilon. \end{align*} $$
In this notation, the CPC states that
![]() $\varepsilon =\frac 12$
. Our Main Theorem 1.2 and especially the “t-thin or t-flat” Theorem 1.3 are the first effective bounds for
$\varepsilon =\frac 12$
. Our Main Theorem 1.2 and especially the “t-thin or t-flat” Theorem 1.3 are the first effective bounds for
![]() $\varepsilon>0$
. More precisely, here we prove
$\varepsilon>0$
. More precisely, here we prove
![]() $\varepsilon = \Omega \big (\frac {1}{n}\big )$
for all posets, and a constant lower bound on
$\varepsilon = \Omega \big (\frac {1}{n}\big )$
for all posets, and a constant lower bound on
![]() $\varepsilon $
for posets with bounded parameter t. Improving these bounds seems an interesting challenging problem even if the CPC ultimately fails.
$\varepsilon $
for posets with bounded parameter t. Improving these bounds seems an interesting challenging problem even if the CPC ultimately fails.
8.4
The constant
![]() $\frac 12$
in Favard’s inequality has the same nature as the constant
$\frac 12$
in Favard’s inequality has the same nature as the constant
![]() $2$
in [Reference Ross, Suss and WannererRSW23, Corollary 1.5] which also follows from Favard’s inequality written in terms of the Lorentzian polynomials technology. The relationships to the constant 2 in [Reference Chan and PakCP22b, Theorem 1.1] and [Reference Huh, Schröter and WangHSW22, Theorem 5] are more distant, but fundamentally of the same nature. While in the former case it is tight, in the latter is likely much smaller (see [Reference HuhHuh18, Section 2.3]).
$2$
in [Reference Ross, Suss and WannererRSW23, Corollary 1.5] which also follows from Favard’s inequality written in terms of the Lorentzian polynomials technology. The relationships to the constant 2 in [Reference Chan and PakCP22b, Theorem 1.1] and [Reference Huh, Schröter and WangHSW22, Theorem 5] are more distant, but fundamentally of the same nature. While in the former case it is tight, in the latter is likely much smaller (see [Reference HuhHuh18, Section 2.3]).
8.5
The reader might find surprising the discrepancy between the vanishing and the nonvanishing cases in the Main Theorem 1.2. Note that the vanishing case actually implies a worse bound (1.2) compared to the bound (1.1) in the nonvanishing case, instead of making things simpler. This is an artifact of the mixed volume inequalities and combinatorial ratios. Proposition 6.3 gives a better bound than Proposition 6.4 simply because the ratio of
![]() $\textrm {F}(\cdot ,\cdot )$
’s in the former is under a square root which decreases the order. However, these combinatorial bounds can only be applied when the corresponding terms are nonzero.
$\textrm {F}(\cdot ,\cdot )$
’s in the former is under a square root which decreases the order. However, these combinatorial bounds can only be applied when the corresponding terms are nonzero.
Clearly, there is no way to justify this discrepancy, as otherwise we would know how to disprove the CPC. Still, one can ask if there is another approach to the vanishing case which would improve the bound? We caution the reader that sometimes nonvanishing does indeed make a difference (see, e.g., Example 4.5).
8.6
Theorem 4.1 gives the vanishing conditions for the generalized Stanley inequalities. It was first stated without a proof in [Reference Daykin and DaykinDD85, Theorem 8.2], and it seems the authors were aware of a combinatorial proof by analogy with their proof of the corresponding results for the order polynomial. The theorem was rediscovered in [Reference Chan, Pak and PanovaCPP23a, Theorem 1.12], where it was proved via combinatorics of words. Independently, it was also proved by a geometric argument in [Reference Shenfeld and van HandelSvH23, Lemma 15.2] for Stanley’s inequality, and in [Reference Ma and ShenfeldMS24, Theorem 5.3] for generalized Stanley’s inequality.
8.7
There is a large literature on the negative dependence in a combinatorial context (see, e.g., [Reference Borcea, Brändén and LiggettBBL09, Reference HuhHuh18, Reference PemantlePem00]), and in the context of linear extensions [Reference Kahn and YangKY98, Reference SheppShe82]. When it comes to correlation inequalities for linear extensions of posets, this paper can be viewed as the third in a series after [Reference Chan and PakCP22b] and [Reference Chan and PakCP23a] by the first two authors. These papers differ by the tools involved. In [Reference Chan and PakCP22b], we use the combinatorial atlas technology (see [Reference Chan and PakCP21, Reference Chan and PakCP22a]), while in [Reference Chan and PakCP23a] we use the FKG-type inequalities.
The idea of this paper was to use geometric inequalities for mixed volumes, to obtain new cross-product-type inequalities. As we mentioned in the introduction, it transfers the difficulty to the combinatorics of words. This is the approach introduced in [Reference HaimanHai92, Reference Malvenuto and ReutenauerMR94] (see also [Reference StanleySta09]), and advanced in [Reference Chan, Pak and PanovaCPP22, Reference Chan, Pak and PanovaCPP23a, Reference Chan, Pak and PanovaCPP23b] in a closely related context.
8.8
Despite the apparent symmetry between the t-thin and t-flat notions, there is a fundamental difference between them. For posets
![]() $P=(X, \prec )$
which are t-thin with respect to a set A of bounded size, the number
$P=(X, \prec )$
which are t-thin with respect to a set A of bounded size, the number
![]() $e(P)$
of linear extension can be computed in polynomial time, since
$e(P)$
of linear extension can be computed in polynomial time, since
![]() $P':=(X\smallsetminus A,\prec )$
has width at most t. On the other hand, for posets which have bounded height, computing
$P':=(X\smallsetminus A,\prec )$
has width at most t. On the other hand, for posets which have bounded height, computing
![]() $e(P)$
is
$e(P)$
is ![]() -complete [Reference Brightwell and WinklerBW91, Reference Dittmer and PakDP18], and the same holds for posets which are t-flat with respect to a set of bounded size.
-complete [Reference Brightwell and WinklerBW91, Reference Dittmer and PakDP18], and the same holds for posets which are t-flat with respect to a set of bounded size.
Acknowledgments
We are grateful to Jeff Kahn, Yair Shenfeld, and Ramon van Handel for many helpful discussions and remarks on the subject, and to Julius Ross for telling us about [Reference Ross, Suss and WannererRSW23]. We are thankful to Per Alexandersson for providing Mathematica packages to test the conjectures.