Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sauer, Norbert
1998.
Edge partitions of the countable triangle free homogeneous graph.
Discrete Mathematics,
Vol. 185,
Issue. 1-3,
p.
137.
2000.
Theory of Relations.
Vol. 145,
Issue. ,
p.
417.
El-Zahar, Mohamed
and
Sauer, N.W.
2005.
Indivisible homogeneous directed graphs and a game for vertex partitions.
Discrete Mathematics,
Vol. 291,
Issue. 1-3,
p.
99.
Laflamme, C.
Nguyen Van Thé, L.
Pouzet, M.
and
Sauer, N.
2011.
Partitions and indivisibility properties of countable dimensional vector spaces.
Journal of Combinatorial Theory, Series A,
Vol. 118,
Issue. 1,
p.
67.
Meir, Nadav
2015.
Many symmetrically indivisible structures.
Mathematical Logic Quarterly,
Vol. 61,
Issue. 4-5,
p.
341.
MEIR, NADAV
2016.
ON PRODUCTS OF ELEMENTARILY INDIVISIBLE STRUCTURES.
The Journal of Symbolic Logic,
Vol. 81,
Issue. 3,
p.
951.
Meir, Nadav
2022.
Infinite lexicographic products.
Annals of Pure and Applied Logic,
Vol. 173,
Issue. 1,
p.
102991.

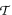 be a finite set of finite tournaments. We will give a necessary and sufficient condition for the
be a finite set of finite tournaments. We will give a necessary and sufficient condition for the 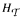 to be divisible. That is, that there is a partition of
to be divisible. That is, that there is a partition of 