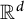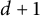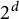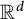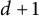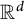On the general dyadic grids on ${\mathbb {R}}^d$

Abstract

Adjacent dyadic systems are pivotal in analysis and related fields to study continuous objects via collections of dyadic ones. In our prior work (joint with Jiang, Olson, and Wei), we describe precise necessary and sufficient conditions for two dyadic systems on the real line to be adjacent. Here, we extend this work to all dimensions, which turns out to have many surprising difficulties due to the fact that $d+1$, not $2^d$, grids is the optimal number in an adjacent dyadic system in $\mathbb {R}^d$. As a byproduct, we show that a collection of $d+1$ dyadic systems in $\mathbb {R}^d$ is adjacent if and only if the projection of any two of them onto any coordinate axis are adjacent on $\mathbb {R}$. The underlying geometric structures that arise in this higher-dimensional generalization are interesting objects themselves, ripe for future study; these lead us to a compact, geometric description of our main result. We describe these structures, along with what adjacent dyadic (and n-adic, for any n) systems look like, from a variety of contexts, relating them to previous work, as well as illustrating a specific exa.

1 Introduction

The purpose of this paper is to give an optimal description of adjacent dyadic systems (or more generally, adjacent n-adic systems) in $\mathbb {R}^d$ . Dyadic systems are ubiquitous in harmonic analysis, as well as many other fields. Oftentimes, one wants to understand a continuous operator or object via its dyadic counterparts; our goal is to say, in an optimal and precise fashion, exactly what these dyadic counterparts are.

The study of continuous objects via dyadic ones is a central theme in analysis and its application to many different areas of mathematics. For instance, dyadic decompositions and partitions underlie the study of singular integral operators and maximal functions (among others), weight and function classes, partial differential equations, and number theory; our bibliography lists a few out of many references here. In our recent paper [2] joint with Jiang, Olson, and Wei, we gave a necessary and sufficient condition on characterizing the adjacent n-adic systems on $\mathbb {R}$ . Here, we generalize these results to higher dimensions. Although we use ideas from [2], the construction of the analogous objects in $\mathbb {R}^d$ is not trivial; indeed, we have to adapt our techniques from [2] to a way that is compatible with the underlying lattice structure inherent in the construction of adjacent n-adic systems in $\mathbb {R}^d$ .

Let us begin with the definition of n-adic systems in $\mathbb {R}^d$ , which is our main object of study.

Definition 1.1 Given $n \in {\mathbb N}, n \ge 2$ , a collection ${\mathcal G}$ of left-closed and right-open cubes on $\mathbb {R}^d$ (that is, a collection of cubes in $\mathbb {R}^d$ of the form

$$ \begin{align*}[a_1, a_1+\ell) \times \dots \times [a_d, a_d+\ell), \quad a_i \in \mathbb{R}, i=1, \dots, d, \end{align*} $$

where $\ell>0$ is the sidelength of such a cube) is called a general dyadic grid with base n (or n-adic grid) if the following conditions are satisfied:

1. (i) For any $Q \in {\mathcal G}$ , its sidelength $\ell (Q)$ is of the form $n^k, k \in \mathbb {Z}$ .

2. (ii) $Q \cap R \in \{Q, R, \emptyset \}$ for any $Q, R \in {\mathcal G}$ .

3. (iii) For each fixed $k\in \mathbb {Z}$ , the cubes of a fixed sidelength $n^k$ form a partition of $\mathbb {R}^d$ .

In particular, if $n=2$ , we also refer to such a collection a dyadic grid, which is usually denoted by ${\mathcal D}$ .

The defining property of such a structure is a certain dyadic covering theorem. The one that we use is due to Conde Alonso [5], and is optimal in terms of the number of grids required.

Theorem 1.2 [5, Theorem 1.1]

There exist $d+1$ dyadic grids ${\mathcal D}_1, \dots , {\mathcal D}_{d+1}$ of $\mathbb {R}^d$ such that every Euclidean ball B (or every cube) is contained in some cube $Q \in \bigcup \limits _{i=1}^{d+1} {\mathcal D}_i$ satisfying that $\textrm {diam}(Q) \le C_d \textrm {diam}(B)$ . The number of dyadic systems is optimal.

We make a remark that the optimal number $d+1$ in Theorem 1.2 plays an important role throughout this paper. Motivated by Theorem 1.2, we introduce the following definition of adjacent n-dic systems in $\mathbb {R}^d$ , our main object of study.

Definition 1.3 Given $d+1$ many ${\mathcal G}_1, \dots , {\mathcal G}_{d+1}\ n$ -adic grids, we say that they are adjacent if, for any cube $Q \subseteq \mathbb {R}^d$ (or any ball), there exists $i \in \{1, \dots , d+1\}$ , and $R \in {\mathcal G}_i$ , such that:

1. (1) $Q \subseteq R$ ;

2. (2) $\ell (R) \le C_{d, n}\ell (Q)$ , where $C_{d, n}$ is a dimension constant that only depends on d and n.

This characterizing property of adjacent dyadic systems is sometimes referred to as Mei’s lemma due to the work [13] on the torus (hence, the definition we use is sometimes called the optimal Mei’s lemma). This property has been widely explored in a wide array of contexts and settings (see [9, 12, 14]), and has a long history; see the introduction of [2] and also the monographs [6, 11] for details. The applications of Mei’s lemma are vast; adjacent dyadic systems are crucially used in the area of sparse domination (initiated by Lerner to prove the $A_2$ theorem in [10]; see also [4, 7] among others), functional analysis [8, 12, 14], and measure theory [3].

Note that Conde Alonso’s theorem only guarantees the existence of a collection of adjacent dyadic systems in $\mathbb {R}^d$ ; it does not say how to construct such systems in general nor how to tell if a system is adjacent. Inspired by [2], we ask “what are the necessary and sufficient conditions so that a given collection of $d+1\ n$ -adic grids in $\mathbb {R}^d$ is adjacent?”

In [2], we give a complete answer to this question on the real line, which we will briefly review in Section 2. In order to extend these results in [2] to higher dimensions, we must deal with how $d+1\ n$ -adic grids, instead of only 2, interact with each other. The main idea to overcome such a difficulty is to work on a certain quantified version of the n-adic systems. We introduced a one-dimensional analog of this in [2]; however, extending this concept to higher dimensions requires many new ideas. The geometric structures that we define to quantify adjacency collapse into much simpler concepts on the real line, and we provide perspective on this throughout the paper.

1.1 Statement of the main result

Suppose we are given $d+1\ n$ -adic grids ${\mathcal G}_1, \dots , {\mathcal G}_{d+1}$ in $\mathbb {R}^d$ . Here is how to verify whether they are adjacent or not.

Algorithm 1.4 Step I: For each $i \in \{1, \dots , d+1\}$ , write

$$ \begin{align*}{\mathcal G}_i:={\mathcal G}(\delta_i, {\mathcal L}_{{\vec{\textbf{a}}}_i}), \end{align*} $$

where

1. (a) $\delta _i \in \mathbb {R}^d$ is called the initial position of ${\mathcal G}_i$ ;

2. (b) ${\mathcal L}_{{\vec {\textbf {a}}}_i}: {\mathbb N} \to {\mathbb N}^d$ is the called the location function of ${\mathcal G}_i$ , where ${\vec {\textbf {a}}}_i \in \mathbb M_{d \times \infty } (\mathbb {Z}^n)$ is an infinite matrix with d rows, infinitely many columns, and entries belonging to $\mathbb {Z}^n$ .

Here, the term ${\mathcal G}(\delta _i, {\mathcal L}_{{\vec {\textbf {a}}}_i})$ is referred as the representation of the n-adic grid ${\mathcal G}$ (see Section 3 for more detailed information about this concept).

Step II: Apply the following theorem, which is the main result of this paper.

Theorem 1.5 Let $d, n, \delta _i$ , and ${\vec {\textbf {a}}}_i$ be defined as above. Then the n-adic systems ${\mathcal G}(\delta _1, {\mathcal L}_{{\vec {\textbf {a}}}_1}), \dots , {\mathcal G}(\delta _{d+1}, {\mathcal L}_{{\vec {\textbf {a}}}_{d+1}})$ are adjacent if and only if the following conditions hold:

1. (1) For any $\ell _1, \ell _2 \in \{1, \dots , d+1\}$ where $\ell _1 \neq \ell _2$ , and $s \in \{1, \dots , d\}$ , $\left (\delta _{\ell _1} \right )_s-\left (\delta _{\ell _2} \right )_s$ is n-far, that is, there exists some constant $C(\ell _1, \ell _2, s)>0$ , such that for any $m \ge 0$ and $k \in \mathbb {Z}$ , there holds

   $$ \begin{align*}\left| \left(\delta_{\ell_1} \right)_s-\left(\delta_{\ell_2} \right)_s- \frac{k}{n^m}\right| \ge \frac{C(\ell_1, \ell_2, s)}{n^m}. \end{align*} $$

2. (2) For any $k_1, k_2 \in \{1, \dots , d+1\}, k_1 \neq k_2$ , and $s \in \{1, \dots , d\}$ , there holds

   $$ \begin{align*}0< \liminf_{j \to \infty} 1 \le \limsup_{j \to \infty} \left|\frac{ \left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_1}}(j)\right]_{s}-\left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_2}}(j)\right]_{s}}{n^j}\right|<1. \end{align*} $$

Here and in the sequel, we use $(\delta )_s$ to denote the sth component of a vector $\delta \in \mathbb {R}^d$ .

Note that Theorem 1.5 is sharp, in the sense that the number of the dyadic systems is optimal. The proof of the above theorem uses the idea of representation of n-adic grids, which was introduced in [2]. Moreover, combining with the one-dimensional result (see [2, Theorem 3.8] or Theorem 2.2), Theorem 1.5 is equivalent to the following result.

Theorem 1.6 The collection of n-adic systems ${\mathcal G}_1, \dots , {\mathcal G}_{d+1}$ is adjacent if and only if for any $j \in \{1, \dots , d\}$ and $k_1, k_2 \in \{1, \dots ,d+1\}, k_1 \neq k_2$ , $P_j({\mathcal G}_{k_1})$ and $P_j({\mathcal G}_{k_2})$ are adjacent on $\mathbb {R}$ .

Here, $P_j$ is the orthogonal projection onto the jth axis of $\mathbb {R}^d$ , and for any n-adic grid ${\mathcal G}$ , $P_j({\mathcal G})$ is defined to be the collection of all $P_j(Q), Q \in {\mathcal G}$ .

Remark 1.7 Recall that in the classical approach of constructing an adjacent system in $\mathbb {R}^d$ , what we usually do is first take any two adjacent dyadic systems (on $\mathbb {R}$ ) on each coordinate axis, and then take the Cartesian products of these dyadic systems. Note that this will give us a collection of $2^d$ adjacent dyadic systems in $\mathbb {R}^d$ . We would like to point out that Corollary 1.6 does not follow from this classical approach. First of all, our result is optimal, in the sense that the number of the n-adic systems is $d+1$ , rather than $2^d$ ; moreover, our result provides a necessary and sufficient condition to tell whether a collection of $d+1\ n$ -adic grids are adjacent or not, rather than a single construction.

Another interesting question to ask is whether there is a more inherent geometric approach to study the adjacency of the systems of the n-adic grids. More precisely, can we generalize the one-dimensional result (see Theorem 2.2) in a more parallel way, that respects the underlying geometric structure present in $d+1$ adjacent dyadic systems?

In the second part of this paper, we give an affirmative and precise answer to the above question. The key idea is to introduce the so-called fundamental structures of a collection of $d+1\ n$ -adic grids in $\mathbb {R}^d$ . These basic structures allow us to generalize the one-dimensional result (see Theorem 2.2) in a more heuristic way (see Theorem 8.1), whereas Theorem 1.5 is much less obviously connected with the geometry of adjacent dyadic systems. The intuition for introducing these structures comes from a first, natural attempt to generalize the results in [2] to $\mathbb {R}^d$ (see Remark 7.10 and Section 8.1). Furthermore, all of these constructions are illustrated by a concrete example, which is elaborated on in detail before the proof of the main result (see Theorem 8.1). This allows the reader to connect the underlying geometry with the results and examples in [2] in a concrete way.

The novelty in this paper is that we generalize the results in [2] via two different ways that retain the key lattice structure implicit in the proof of [5] for $d+1$ grids. These generalizations are nontrivial, and motivate us to look at the underlying lattice structures inherent in the construction of $d+1$ grids and to expand them in a manner adaptable to the constructions underlying the main result (Theorem 3.8) in [2]. These constructions allow us to better connect the geometry of the lattice with the arithmetic properties outlined in Theorem 8.1, and likely will have applications to a variety of other problems in dyadic harmonic analysis.

The outline of this paper is as follows. Part I begins with a brief reminder of our one-dimensional results, followed by relevant definitions to state and prove our main theorem on necessary and sufficient conditions for adjacency—this statement mirrors the one-dimensional results only in notation, and does not shed light at the interesting geometric interactions taking place. Therefore, Part II is devoted to studying these. Part II fully describes the rich geometry underlying the main result, including the fundamental structures which we define. These descriptions not only motivate a restating of our main result that is geometrically driven, but provide a clear (and unifying) relationship between our one-dimensional result and higher dimensions. They also allow us to comment on the uniformity of such representations. Finally, we illustrate everything with a concrete example, first introduced in Part I and revisited in Part II.

Part 1. Background and the proof of the main result

In the first part of this paper, we first make a short review of the one-dimensional results, which were considered in [2]. Then, using the idea of representation of n-adic grids, we prove Theorem 1.5. Finally, we give an example on how to apply our main result.

2 One-dimensional results and some application

Let us make a brief review of the case $d=1$ , which was considered in our early work [2]. The main question that was under the consideration in [2] is the following “Given two n-adic grids ${\mathcal G}_1$ and ${\mathcal G}_2$ on $\mathbb {R}$ , what is the necessary and sufficient condition so that they are adjacent?”

We start with recalling the following definition.

Definition 2.1 A real number $\delta $ is n-far if there exists $C>0$ such that

(2.1) $$ \begin{align} \left| \delta-\frac{k}{n^m} \right| \ge \frac{C}{n^m}, \quad \forall m \ge 0, k \in \mathbb{Z}, \end{align} $$

where C may depend on $\delta $ but independent of m and k.

The key idea in [2] to study this problem is to quantify each n-adic grids. More precisely, for any n-adic system ${\mathcal G}$ on $\mathbb {R}$ , we can find a number $\delta \in \mathbb {R}$ , and an infinite sequence $\textbf {a}:=\{a_0, a_1, \dots , a_j, \dots \} \in \{0, \dots , n-1\}^\infty $ , such that ${\mathcal G}$ can be represented as ${\mathcal G}(\delta , {\mathcal L}_{\mathrm {\mathbf {a}}})$ , where ${\mathcal L}_{\mathrm {\mathbf {a}}}: {\mathbb N} \to {\mathbb N}$ is called the location function associated to a , which is defined as

$$ \begin{align*}{\mathcal L}_{\mathrm {\mathbf{a}}}(j):=\sum_{k=0}^{j-1} a_i n^k, \quad j \ge 1, \end{align*} $$

and ${\mathcal L}_{\mathrm {\mathbf {a}}}(0)=0$ .

Given two n-adic systems ${\mathcal G}_1$ and ${\mathcal G}_2$ , let us write them as ${\mathcal G}_1={\mathcal G}(\delta _1, {\mathcal L}_{\mathrm {\mathbf {a}}_1})$ and ${\mathcal G}_2={\mathcal G}(\delta _2, {\mathcal L}_{\mathrm {\mathbf {a}}_2})$ . Here is the main result in [2].

Theorem 2.2 [2, Theorem 3.8]

The n-adic grids ${\mathcal G}(\delta _1, {\mathcal L}_{\mathrm {\mathbf {a}}_1})$ and ${\mathcal G}(\delta _2, {\mathcal L}_{\mathrm {\mathbf {a}}_2})$ are adjacent if and only if:

1. (1) $\delta _1-\delta _2$ is n-far.

2. (2) There exists some $0<C_1 \le C_2<1$ , such that

   $$ \begin{align*}0<C_1=\liminf_{j \to \infty} \left| \frac{{\mathcal L}_{\mathrm {\mathbf{a}}_1}(j)-{\mathcal L}_{\mathrm {\mathbf{a}}_2}(j)}{n^j} \right| \le \limsup_{j \to \infty} \left| \frac{{\mathcal L}_{\mathrm {\mathbf{a}}_1}(j)-{\mathcal L}_{\mathrm {\mathbf{a}}_2}(j)}{n^j} \right|=C_2<1. \end{align*} $$

Remark 2.3 To check whether $\delta _1-\delta _2$ is n-far or not, it suffices to check whether $T\left ( \{\delta _1-\delta _2\} \right )$ is finite or not, where $\{\cdot \}$ indicates distance to the nearest integer, and for any $\delta \in [0, 1)$ , $T(\delta )$ is defined to be the maximal length of consecutive $0$ ’s or ( $n-1$ )’s in the base n representation of $\delta $ (see [2, Theorem 2.8]).

Although the representation of an n-adic grid is indeed not unique (see the remark after [2, Definition 3.11] for the case $d=1$ , or see Proposition 3.3 for the general case), Theorem 2.2 still enjoys some uniformness property.

Theorem 2.4 [2, Theorem 3.14]

Under the same assumption of Theorem 2.2, let ${\mathcal G}(\delta ^{\prime }_1, {\mathcal L}_{\mathrm {\mathbf {a}}^{\prime }_1})$ and ${\mathcal G}(\delta ^{\prime }_2, {\mathcal L}_{\mathrm {\mathbf {a}}^{\prime }_2})$ be some other representations of ${\mathcal G}_1$ and ${\mathcal G}_2$ , respectively. Then either

$$ \begin{align*}\liminf_{j \to \infty} \left| \frac{{\mathcal L}_{\mathrm {\mathbf{a}}^{\prime}_1}(j)-{\mathcal L}_{\mathrm {\mathbf{a}}^{\prime}_2}(j)}{n^j} \right|=C_1 \quad \textrm{and} \quad \limsup_{j \to \infty} \left| \frac{{\mathcal L}_{\mathrm {\mathbf{a}}^{\prime}_1}(j)-{\mathcal L}_{\mathrm {\mathbf{a}}^{\prime}_2}(j)}{n^j} \right|=C_2 \end{align*} $$

or

$$ \begin{align*}\liminf_{j \to \infty} \left| \frac{{\mathcal L}_{\mathrm {\mathbf{a}}^{\prime}_1}(j)-{\mathcal L}_{\mathrm {\mathbf{a}}^{\prime}_2}(j)}{n^j} \right|=1-C_2 \quad \textrm{and} \quad \limsup_{j \to \infty} \left| \frac{{\mathcal L}_{\mathrm {\mathbf{a}}^{\prime}_1}(j)-{\mathcal L}_{\mathrm {\mathbf{a}}^{\prime}_2}(j)}{n^j} \right|=1-C_1. \end{align*} $$

With the help of Theorem 1.6, we can easily generalize Theorem 2.4 to higher dimensions.

Corollary 2.5 Under the same assumption of Theorem 1.5, let

$$ \begin{align*}{\mathcal G}(\delta_1', {\mathcal L}_{{\vec{\textbf{a}}}_1'}), \dots , {\mathcal G}(\delta_{d+1}', {\mathcal L}_{{\vec{\textbf{a}}}_{d+1}'})\end{align*} $$

be some other representations of ${\mathcal G}_1, \dots , {\mathcal G}_{d+1}$ , respectively. Moreover, for each $k_1, k_2 \in \{1, \dots , d+1\}$ and $s \in \{1, \dots , d\}$ , denote

$$ \begin{align*}D_1(k_1, k_2, s):=\liminf_{j \to \infty} \left|\frac{ \left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_1}}(j)\right]_{s}-\left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_2}}(j)\right]_{s}}{n^j}\right|, \end{align*} $$

$$ \begin{align*}D_2(k_1, k_2, s):=\limsup_{j \to \infty} \left|\frac{ \left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_1}}(j)\right]_{s}-\left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_2}}(j)\right]_{s}}{n^j}\right|, \end{align*} $$

and $D_1'(k_1, k_2, s), D_2'(k_1, k_2, s)$ similarly, then either

$$ \begin{align*}D_1'(k_1, k_2, s)=D_1(k_1, k_2, s) \quad \textrm{and} \quad D_2'(k_1, k_2, s)=D_2(k_1, k_2, s) \end{align*} $$

or

$$ \begin{align*}D_1'(k_1, k_2, s)=1-D_2(k_1, k_2, s) \quad \textrm{and} \quad D_2'(k_1, k_2, s)=1-D_1(k_1, k_2, s). \end{align*} $$

Proof Corollary 2.5 is an easy consequence of Theorems 1.5 and 1.6, and we would like to leave the detail to the interested reader.

3 Representation of $n$ -adic grids

Let us extend the concept of the representation of n-adic grids to higher dimension. The setting is as follows.

1. (1) $\delta \in \mathbb {R}^d$ , in particular, $\delta $ should be thought as a vertex of some cube belonging to the zeroth generation, and we may think it as the “initial point” of our n-adic system.

2. (2) An infinite matrix

   (3.1) $$ \begin{align} \vec{\textbf{a}}:=\left\{\vec{a}_0, \dots, \vec{a}_j, \dots \right\}, \end{align} $$
   where $\vec {a}_j \in \{0,1,\dots , n-1\}^d, j \ge 1$ .

3. (3) The location function associated to $\vec {\textbf {a}}$ :

   $$ \begin{align*}{\mathcal L}_{{\vec{\textbf{a}}}}: {\mathbb N} \longmapsto \mathbb{Z}^d, \end{align*} $$
   which is defined by
   $$ \begin{align*}{\mathcal L}_{{\vec{\textbf{a}}}}(j):= \begin{cases} \sum\limits_{i=0}^{j-1} n^i\vec{a}_i, \hfill \quad \quad \quad j \ge 1.\\ \\ \vec{0}, \hfill \quad \quad \quad j=0. \end{cases} \end{align*} $$

For a vector $\delta \in \mathbb {R}^d$ , we use the notation $(\delta )_i, 1 \le i \le d$ , refers to the ith component of $\delta $ . Note that we will frequently be working with sets of d vectors in $\mathbb {R}^d$ , which we label $\delta _1, \dots , \delta _d$ . Therefore, the parentheses distinguish the selection from the components: $(\delta _i)_s$ is the sth component of the vector $\delta _i$ .

Definition 3.1 Let $\delta \in \mathbb {R}^d$ , ${\vec {\textbf {a}}}$ , and ${\mathcal L}_{{\vec {\textbf {a}}}}$ be defined as above. Let ${\mathcal G}(\delta , {\mathcal L}_{{\vec {\textbf {a}}}})$ be the collection of the following cubes:

1. (1) For $m \ge 0$ , the mth generation of ${\mathcal G}(\delta , {\mathcal L}_{{\vec {\textbf {a}}}})$ is defined as

   $$ \begin{align*} {\mathcal G}(\delta)_m :={\mathcal G}(\delta, {\mathcal L}_{{\vec{\textbf{a}}}})_m &:=\Bigg\{ \left[ (\delta)_1+\frac{k_1}{n^m}, (\delta)_1+\frac{k_1+1}{n^m} \right) \times \cdots \\ & \quad \times \left[ (\delta)_d+\frac{k_d}{n^m}, (\delta)_d+\frac{k_d+1}{n^m} \right) \bigg | (k_1, \dots, k_d) \in \mathbb{Z}^d \Bigg\}. \end{align*} $$

   We make a remark and sometimes we drop the dependence of the location function here, since location function only contributes to the negative generations.

2. (2) For $m<0$ , the mth generation is defined as

   $$ \begin{align*} & {\mathcal G}(\delta, {\mathcal L}_{{\vec{\textbf{a}}}})_m:=\Bigg\{ \left[ (\delta)_1+\left[ {\mathcal L}_{{\vec{\textbf{a}}}}(-m) \right]_1+\frac{k_1}{n^m}, (\delta)_1+\left[ {\mathcal L}_{{\vec{\textbf{a}}}}(-m) \right]_1+\frac{k_1+1}{n^m} \right) \times \cdots \nonumber \\ & \times \left[ (\delta)_d+\left[ {\mathcal L}_{{\vec{\textbf{a}}}}(-m) \right]_d+\frac{k_d}{n^m}, (\delta)_d+\left[ {\mathcal L}_{{\vec{\textbf{a}}}}(-m) \right]_d+\frac{k_d+1}{n^m} \right) \bigg | (k_1, \dots, k_d) \in \mathbb{Z}^d \Bigg\}. \end{align*} $$

Or equivalently:

1. (1) For $m \ge 0$ , the vertices of all mth generation are defined as

   $$ \begin{align*}{\mathcal A}(\delta)_m:={\mathcal A}(\delta, {\mathcal L}_{{\vec{\textbf{a}}}})_m:=\left\{ \delta+\frac{\vec{k}}{n^m}, \vec{k} \in \mathbb{Z}^d \right\}. \end{align*} $$

2. (2) For $m<0$ , the vertices of all mth generation are defined as

   $$ \begin{align*}{\mathcal A}(\delta, {\mathcal L}_{{\vec{\textbf{a}}}})_m:=\left\{ \delta+ {\mathcal L}_{{\vec{\textbf{a}}}}(-m)+\frac{\vec{k}}{n^m}, \vec{k} \in \mathbb{Z}^d \right\}. \end{align*} $$

Note that in the above definition, the term $\delta +{\mathcal L}_{{\vec {\textbf {a}}}}(-m)$ can be interpreted as the location of the “initial point” (that is, $\delta \in {\mathcal A}(\delta , {\mathcal L}_{{\vec {\textbf {a}}}})_0$ ) after choosing n-adic parents (with respect to the zeroth generation) $(-m)$ times.

Proposition 3.2 ${\mathcal G}(\delta , {\mathcal L}_{{\vec {\textbf {a}}}})$ is an n-adic grid in $\mathbb {R}^d$ .

Proof If we restrict the grid to each axis, we obtain an n-adic grid with respect to that axis [2]. Since cubes are a one-parameter family, one can easily see (by contradiction) that cubes of a given level tile the space, two cubes are either contained one in the other or disjoint, and each cube has $n^d$ children (each with $1/n^d$ of its parent’s size) and exactly one parent.

Proposition 3.3 Given any n-adic grid ${\mathcal G}$ , we can find a $\delta \in \mathbb {R}^d$ and an infinite matrix ${\vec {\textbf {a}}}=\{\vec {a}_0, \dots , \vec {a}_j, \dots \}$ , where $\vec {a}_j \in \{0, \dots , d-1\}^d, j \ge 1$ , such that

$$ \begin{align*}{\mathcal G}={\mathcal G}(\delta, {\mathcal L}_{{\vec{\textbf{a}}}}). \end{align*} $$

However, this representation may not be unique.

Proof The proof of this result is an easy modification of [2, Proposition 4.10], and hence we leave the detail to the interested reader. While the fact that such a representation is not unique is also straightforward, one example in $\mathbb {R}^d$ would be

$$ \begin{align*}{\mathcal G}\left( (0, 0), {\mathcal L}_{{\vec{\textbf{a}}}_1} \right)={\mathcal G}\left(\left(2, 2 \right), {\mathcal L}_{{\vec{\textbf{a}}}_2}\right), \end{align*} $$

where

$$ \begin{align*}{\vec{\textbf{a}}}_1=\begin{pmatrix} 1 & 0 & 0 & 0 & \dots\\ 1 & 0 & 0 & 0 & \dots \end{pmatrix} \quad \textrm{and} \quad {\vec{\textbf{a}}}_2=\begin{pmatrix} 0 & n-1 & n-1 & n-1 & \dots\\ 0 & n-1 & n-1 & n-1 & \dots \end{pmatrix}. \end{align*} $$

4 Proof of the main result

In this section, we prove the main result Theorem 1.5.

4.1 Necessity

Suppose ${\mathcal G}_1={\mathcal G}(\delta _1, {\mathcal L}_{{\vec {\textbf {a}}}_1}), \dots , {\mathcal G}_{d+1}={\mathcal G}(\delta _{d+1}, {\mathcal L}_{{\vec {\textbf {a}}}_{d+1}})$ are adjacent. We prove the necessary part by contradiction.

Assume condition (a) fails, that is, there exists some $\ell _1, \ell _2 \in \{1, \dots , d+1\}$ with $\ell _1 \neq \ell _2$ and $s \in \{1, \dots , d\}$ , such that for each $N_1 \ge 1$ , there exists some $m_1 \ge 0$ and $K \in \mathbb {Z}$ , such that

$$ \begin{align*}\left| \left(\delta_{\ell_1} \right)_s-\left(\delta_{\ell_2} \right)_s- \frac{K}{n^{m_1}}\right|< \frac{1}{N_1 n^{m_1}}, \end{align*} $$

which implies that the distance between the hyperplane $\left \{(x)_s=(\delta _{\ell _1})_s\right \}$ and the hyperplane $\left \{(x)_s=(\delta _{\ell _2})_s+K/n^{m_1}\right \}$ is less than $1/(N_1 n^{m_1})$ . On the other hand, note that

$$ \begin{align*}\left\{(x)_s=(\delta_{\ell_1})_s\right\} \subset b\left[ {\mathcal G}_{\ell_1, {m_1}} \right] \end{align*} $$

and

$$ \begin{align*}\left\{(x)_s=(\delta_{\ell_2})_s+\frac{K}{n^{m_1}}\right\} \subset b\left[ {\mathcal G}_{\ell_2, {m_1}} \right], \end{align*} $$

where $b\left [ {\mathcal G}_{\ell _1, m_1} \right ]$ is the union of all the boundaries of the cubes in ${\mathcal G}_{\ell _1}$ with sidelength $1/n^{m_1}$ , and similarly for the term $b\left [ {\mathcal G}_{\ell _2, m_1} \right ]$ .

Now, the idea is to find two sufficiently closed points on the intersection of the boundaries of these n-adic grids. Without loss of generality, let us assume $s=\ell _1=1$ and $\ell _2=2$ . Now, let us consider the points

$$ \begin{align*}p_1:=\{(x)_1=(\delta_1)_1\} \cap \{(x)_2=(\delta_3)_2 \} \cap \cdots \cap \{(x)_d=(\delta_{d+1})_d \} \end{align*} $$

and

$$ \begin{align*}p_2:=\left\{(x)_1=(\delta_2)_1+\frac{K}{n^{m_1}}\right\} \cap \{(x)_2=(\delta_3)_2 \} \cap \cdots \cap \{(x)_d=(\delta_{d+1})_d \} \}, \end{align*} $$

which satisfy the following properties:

1. (a) $p_1 \in b\left [ {\mathcal G}_{1, m_1} \right ] \cap \bigcap \limits _{t=3}^{d+1} b\left [ {\mathcal G}_{t, m_1} \right ]$ and $p_2 \in \bigcap \limits _{t=2}^{d+1} b\left [ {\mathcal G}_{t, m_1} \right ]$ .

2. (b) $\textrm {dist}(p_1, p_2)=\left | \left (\delta _1 \right )_1-\left (\delta _2 \right )_1- K/n^m\right |< 1/(N_1 n^{m_1})$ .

Note that property (b) above allows us to choose an open cube Q of radius $1/(N_1 n^{m_1})$ that containing both $p_1$ and $p_2$ , whereas property (a) asserts that if there is a dyadic cube $D \in {\mathcal G}_{\ell }, \ell \in \{1, \dots , d+1\}$ covering Q, then $\ell (D)>1/n^{m_1}$ , and hence

$$ \begin{align*}\ell(D)>N_1 \ell(Q). \end{align*} $$

This will contradict to the second condition in Definition 1.3 if we choose $N_1$ sufficiently large (see Figure 1).

Figure 1: $p_1$ , $p_2$ , the hyperplane $\{(x)_1=(\delta _1)_1\}$ (red part), the hyperplane $\left \{(x)_1=(\delta _2)_1+K/n^{m_1}\right \}$ (blue part), the line $L:=\{(x)_2=(\delta _3)_2 \} \cap \cdots \cap \{(x)_d=(\delta _{d+1})_d \}$ , and the cube Q containing both $p_1$ and $p_2$ .

Next, expecting a contradiction again, we assume (b) fails. The proof for this part is very similar to the previous one. Let us consider two different cases.

Case I: There exists some $k_1, k_2 \in \{1, \dots , d+1\}, k_1 \neq k_2$ , and $s \in \{1, \dots , d\}$ , such that

(4.1) $$ \begin{align} \liminf_{j \to \infty} \left|\frac{ \left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_1}}(j)\right]_{s}-\left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_2}}(j)\right]_{s}}{n^j}\right|=0. \end{align} $$

Again, for simplicity, we may assume $s=k_1=1$ and $k_2=2$ . By (4.1), for any $\varepsilon>0$ , there exists some $j_1$ sufficiently large, such that

$$ \begin{align*}\left| \left[{\mathcal L}_{{\vec{\textbf{a}}}_1}(j_1)\right]_1-\left[{\mathcal L}_{{\vec{\textbf{a}}}_2}(j_1)\right]_1 \right|<\varepsilon \cdot n^{j_1}, \end{align*} $$

which implies that

$$ \begin{align*}\left|\left[\delta_1+{\mathcal L}_{{\vec{\textbf{a}}}_1}(j_1)\right]_1-\left[\delta_2+{\mathcal L}_{{\vec{\textbf{a}}}_2}(j_1)\right]_1 \right|<2\varepsilon \cdot n^{j_1}, \end{align*} $$

since we assume $j_1$ is sufficiently large. Now, we can exactly follow the idea in part (a) now. More precisely, we define

$$ \begin{align*}q_1:=\{(x)_1=\left[\delta_1+{\mathcal L}_{{\vec{\textbf{a}}}_1}(j_1)\right]_1\} \cap \bigcup_{t=2}^d \left\{(x)_t=\left[\delta_{t+1}+{\mathcal L}_{{\vec{\textbf{a}}}_{t+1}}(j_1) \right]_t \right\} \end{align*} $$

and

$$ \begin{align*}q_2:= \bigcup_{t=1}^d \left\{(x)_t=\left[\delta_{t+1}+{\mathcal L}_{{\vec{\textbf{a}}}_{t+1}}(j_1) \right]_t \right\}, \end{align*} $$

which enjoy similar properties as $p_1$ and $p_2$ :

1. (a) $q_1 \in b\left [ {\mathcal G}_{1, -j_1} \right ] \cap \bigcap \limits _{k=3}^{d+1} b\left [ {\mathcal G}_{k, -j_1} \right ]$ and $q_2 \in \bigcap \limits _{k=2}^{d+1} b\left [ {\mathcal G}_{k, -j_1} \right ]$ .

2. (b) $\textrm {dist}(q_1, q_2)<2 \varepsilon \cdot n^{j_1}$ .

Then desired contradiction will follow by taking an open cube with sidelength $2\varepsilon \cdot n^{j_1}$ containing both $q_1$ and $q_2$ , where $\varepsilon $ is sufficiently small.

Case II: There exists some $k_1, k_2 \in \{1, \dots , d+1\}, k_1 \neq k_2$ , and $s \in \{1, \dots , d\}$ , such that

(4.2) $$ \begin{align} \limsup_{j \to \infty} \left|\frac{ \left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_1}}(j)\right]_{s}-\left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_2}}(j)\right]_{s}}{n^j}\right|=1. \end{align} $$

The proof for the second case is an easy modification of the first one. Indeed, (4.2) implies that for any $\varepsilon>0$ , there exists some $j_2$ sufficiently large, such that either

$$ \begin{align*}\left| \left[\delta_{k_1}+{\mathcal L}_{{\vec{\textbf{a}}}_{k_1}}(j_2)\right]_{s}-\left[\delta_{k_2}+{\mathcal L}_{{\vec{\textbf{a}}}_{k_2}}(j_2)+n^j \vec{e}_s\right]_{s} \right|<\varepsilon \cdot n^{j_2} \end{align*} $$

or

$$ \begin{align*}\left| \left[\delta_{k_1}+{\mathcal L}_{{\vec{\textbf{a}}}_{k_1}}(j_2)\right]_{s}-\left[\delta_{k_2}+{\mathcal L}_{{\vec{\textbf{a}}}_{k_2}}(j_2)-n^j \vec{e}_s\right]_{s} \right|<\varepsilon \cdot n^{j_2} \end{align*} $$

holds, where in the above estimates, $\vec {e}_s$ refers to the stand unit vector in $\mathbb {R}^d$ with the sth entry being $1$ . The rest of the proof is the same as Case I.

4.2 Sufficiency

Suppose the conditions (a) and (b) hold, that is,

1. (1) For any $\ell _1, \ell _2 \in \{1, \dots , d+1\}$ where $\ell _1 \neq \ell _2$ , and $s \in \{1, \dots , d\}$ , there exists some constant $C(\ell _1, \ell _2, s)>0$ , such that for any $m \ge 0$ and $k \in \mathbb {Z}$ , there holds

   (4.3) $$ \begin{align} \left| \left(\delta_{\ell_1} \right)_s-\left(\delta_{\ell_2} \right)_s- \frac{k}{n^m}\right| \ge \frac{C(\ell_1, \ell_2, s)}{n^m}. \end{align} $$

2. (2) For any $k_1, k_2 \in \{1, \dots , d+1\}, k_1 \neq k_2$ , and $s \in \{1, \dots , d\}$ , there holds

   (4.4) $$ \begin{align} 0< \liminf_{j \to \infty} \left|\frac{ \left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_1}}(j)\right]_{s}-\left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_2}}(j)\right]_{s}}{n^j}\right| \le \limsup_{j \to \infty} \left|\frac{ \left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_1}}(j)\right]_{s}-\left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_2}}(j)\right]_{s}}{n^j}\right|<1. \end{align} $$

Denote

$$ \begin{align*}C_1:=\min_{1 \le \ell_1 \neq \ell_2 \le d+1, 1 \le s \le d} C(\ell_1, \ell_2, s), \quad D_1:=\min_{1 \le k_1 \neq k_2 \le d+1, 1 \le s \le d} D_1(k_1, k_2, s), \end{align*} $$

and

$$ \begin{align*}D_2:=1-\max_{1 \le k_1 \neq k_2 \le d+1, 1 \le s \le d} D_2(k_1, k_2, s), \end{align*} $$

where the quantities $D_1(k_1, k_2, s)$ and $D_2(k_1, k_2, s)$ are defined in Corollary 2.5. Note that $C_1, D_1, D_2>0$ by our assumption (4.4). Moreover, by (4.4), there exists some $N \in {\mathbb N}$ , such that for any $k_1, k_2 \in \{1, \dots , d+1\}, k_1 \neq k_2$ , $s \in \{1, \dots , d\}$ , and $j \ge N$ , there holds

(4.5) $$ \begin{align} \frac{D_1}{2}< \left|\frac{ \left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_1}}(j)\right]_{s}-\left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_2}}(j)\right]_{s}}{n^j}\right|<1-\frac{D_2}{2}. \end{align} $$

Recall that the goal is to show that the collection ${\mathcal G}_1={\mathcal G}(\delta _1, {\mathcal L}_{{\vec {\textbf {a}}}_1}), \dots , {\mathcal G}_{d+1}={\mathcal G}(\delta _{d+1}, {\mathcal L}_{{\vec {\textbf {a}}}_{d+1}})$ is adjacent in $\mathbb {R}^d$ . Take some $C>0$ sufficiently small, such that

$$ \begin{align*}0<C<\min \left\{C_1, \frac{D_1}{4}, \frac{D_2}{4}, \frac{1}{10} \right\}. \end{align*} $$

Now, for any cube Q in $\mathbb {R}^d$ , let $m_0 \in \mathbb {Z}$ such that

$$ \begin{align*}\frac{C}{n^{m_0+1}} \le \ell(Q)<\frac{C}{n^{m_0}}. \end{align*} $$

We consider several cases.

Case I: $m_0>0$ . Let us show that Q is contained in some cube in ${\mathcal G}_{k, m_0}$ for some $k \in \{1, \dots , d+1\}$ . We argue by contradiction. If Q is not contained in any cubes in ${\mathcal G}_{k, m_0}$ for all $k=1, \dots , d+1$ . Then, for each $k \in \{1, \dots , d+1\}$ , there exists some $j_k \in \{1, \dots , d\}$ , such that

$$ \begin{align*}P_{j_k} (Q) \cap P_{j_k} ({\mathcal A}_{k, m_0}) \neq \emptyset, \end{align*} $$

where we recall ${\mathcal A}_{k, m_0}$ is the collection of all the vertices of the cubes in ${\mathcal G}_{k, m_0}$ . By pigeonholing, there exists some $\ell _1, \ell _2 \in \{1, \dots , d+1\}$ with $\ell _1 \neq \ell _2$ , but $j_*:=j_{\ell _1}=j_{\ell _2}$ , such that

$$ \begin{align*}P_{j_*} (Q) \cap P_{j_*} ({\mathcal A}_{\ell_1, m_0}), \quad P_{j_*} (Q) \cap P_{j_*} ({\mathcal A}_{\ell_2, m_0}) \neq \emptyset, \end{align*} $$

which implies that there exists some $K_1, K_2 \in \mathbb {Z}$ , such that

$$ \begin{align*}\left| \left(\delta_{\ell_1}\right)_{j_*}+\frac{K_1}{n^{m_0}} -\left(\delta_{\ell_2} \right)_{j_*}-\frac{K_2}{n^{m_0}} \right| \le \ell(Q)<\frac{C}{n^{m_0}}< \frac{C(\ell_1, \ell_2, j_*)}{n^{m_0}}, \end{align*} $$

which contradicts to (4.3).

Case II: $m_0 \le -N$ . Again, we wish to show that Q is contained in some cubes in ${\mathcal G}_{k, m_0}$ for some $k \in \{1, \dots , d+1\}$ and we prove it by contradiction. Following the argument in Case I above, we see that there exists some $k_1, k_2 \in \{1, \dots , d+1\}$ with $k_1 \neq k_2$ and $j^* \in \{1, \dots , d\}$ , such that

$$ \begin{align*}P_{j^*} (Q) \cap P_{j^*} ({\mathcal A}_{k_1, m_0}), \quad P_{j_*} (Q) \cap P_{j^*} ({\mathcal A}_{k_2, m_0}) \neq \emptyset. \end{align*} $$

This implies that there exists some $K_3, K_4 \in \mathbb {Z}$ , such that

$$ \begin{align*}\left| \left[\delta_{k_1}+{\mathcal L}_{{\vec{\textbf{a}}}_{k_1}}(-m_0) \right]_{j^*}+\frac{K_3}{n^{m_0}}- \left[\delta_{k_2}+{\mathcal L}_{{\vec{\textbf{a}}}_{k_2}}(-m_0) \right]_{j^*}-\frac{K_4}{n^{m_0}} \right|<\frac{C}{n^{m_0}}. \end{align*} $$

Note that since we can always choose N sufficiently large, we can indeed reduce the above estimate to

$$ \begin{align*}\left| \left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_1}}(-m_0) \right]_{j^*}+\frac{K_3}{n^{m_0}}- \left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_2}}(-m_0) \right]_{j^*}-\frac{K_4}{n^{m_0}} \right|<\frac{2C}{n^{m_0}}, \end{align*} $$

which implies that

(4.6) $$ \begin{align} \left| \frac{ \left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_1}}(-m_0) \right]_{j^*}- \left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_2}}(-m_0) \right]_{j^*}}{n^{-m_0}}+(K_3-K_4) \right|< 2C. \end{align} $$

We claim that $K_3-K_4 \in \{-1, 0, 1\}$ . Indeed, by the choice of C, the right-hand side of the above estimate is bounded by $1/5$ ; on the other hand, by the definition of the location function, we have

$$ \begin{align*}\frac{ \left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_1}}(-m_0) \right]_{j^*}- \left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_2}}(-m_0) \right]_{j^*}}{n^{-m_0}} \in (-1, 1). \end{align*} $$

The desired claim then follows from these observations and the fact that $K_3-K_4$ is an integer. Therefore, the estimate (4.6) implies either

$$ \begin{align*}\left| \frac{ \left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_1}}(-m_0) \right]_{j^*}- \left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_2}}(-m_0) \right]_{j^*}}{n^{-m_0}} \right|< 2C<\frac{D_1}{2} \end{align*} $$

or

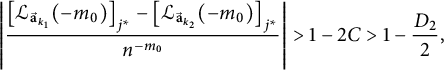$$ \begin{align*}\left| \frac{ \left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_1}}(-m_0) \right]_{j^*}- \left[{\mathcal L}_{{\vec{\textbf{a}}}_{k_2}}(-m_0) \right]_{j^*}}{n^{-m_0}} \right|> 1-2C>1-\frac{D_2}{2}, \end{align*} $$

which contradicts (4.6).

Case III: $-N<m_0 \le 0$ . Indeed, we can “pass” the third case to the second case, by taking a cube $Q'$ containing Q with the sidelength is $n^N$ . Applying the second case to $Q'$ , we find that there exists some $D \in {\mathcal G}_k$ for some $k \in \{1, \dots , d+1\}$ , such that $Q' \subset D$ and $\ell (D) \le C_4 \ell (Q')$ , which clearly implies

1. (1) $Q \subset D$ .

2. (2) $\ell (D) \le C_4 n^N \ell (Q)$ .

The proof is complete.▪

5 An illustrated example

We now take some time to illustrate the effects of this theorem with a concrete example. To begin with, let $\delta _1 = \left (\frac {1}{3}, \frac {1}{3} \right ), \delta _2 = \left ( \frac {2}{3}, \frac {2}{3} \right )$ , $\delta _3 = \left (\frac {1}{5}, \frac {1}{5} \right )$ , $d=2$ , and $n=2$ . Moreover, define the location functions via

$$ \begin{align*}{\vec{\textbf{a}}}_1:= \begin{pmatrix} 1 & 0 & 1 & 0 & \dots\\ 1 & 0 & 1 & 0 & \dots \end{pmatrix}, \end{align*} $$

$$ \begin{align*}{\vec{\textbf{a}}}_2:=\begin{pmatrix} 0 & 1 & 0 & 1 & \dots\\ 0 & 1 & 0 & 1 & \dots \end{pmatrix}, \end{align*} $$

and

$$ \begin{align*}{\vec{\textbf{a}}}_3:=\begin{pmatrix} 0 & 0 & 0 & 0 & \dots\\ 0 & 0 & 0 & 0 & \dots \end{pmatrix}. \end{align*} $$

We will show that the grids ${\mathcal G}_1 = {\mathcal G}(\delta _1, {\mathcal L}_{{\vec {\textbf {a}}}_1})$ , ${\mathcal G}_2 = {\mathcal G}(\delta _2, {\mathcal L}_{{\vec {\textbf {a}}}_2})$ , and ${\mathcal G}_3 = {\mathcal G}(\delta _3, {\mathcal L}_{{\vec {\textbf {a}}}_3})$ form adjacent dyadic systems in $\mathbb {R}^2$ . Note that this example is optimal, in the sense that any two dyadic systems are not adjacent in $\mathbb {R}^2$ .

We start by verifying Condition (i) in Theorem 1.5, which is straightforward. Clearly, it suffices to show the numbers

$$ \begin{align*}\frac{2}{3}-\frac{1}{3}=\frac{1}{3}, \quad \frac{1}{3}-\frac{1}{5}=\frac{2}{15}, \quad \textrm{and} \quad \frac{2}{3}-\frac{1}{5}=\frac{7}{16} \end{align*} $$

are $2$ -far (in the sense of Definition 2.1). This is an easy exercise due to [2, Proposition 2.4] (see also [1, Lemma 3]).

While for the second condition, let us compute all the location functions. Indeed, the cases $j=1,2$ provide the key for the computations.

$$ \begin{align*}\delta_1+{\mathcal L}_{{\vec{\textbf{a}}}_1}(j)= \begin{cases} \left(\frac{2^{j}}{3}, \frac{2^{j}}{3} \right), & \hfill j \ \textrm{even}, \\ \\ \left(\frac{2^{j+1}}{3}, \frac{2^{j+1}}{3} \right), & \hfill j \ \textrm{odd}, \end{cases} \quad \delta_2+{\mathcal L}_{{\vec{\textbf{a}}}_2}(j)= \begin{cases} \left(\frac{2^{j+1}}{3}, \frac{2^{j+1}}{3} \right), & \hfill j \ \textrm{even}, \\ \\ \left(\frac{2^{j}}{3}, \frac{2^{j}}{3} \right), & \hfill j \ \textrm{odd}, \end{cases} \end{align*} $$

and

$$ \begin{align*}\delta_3+{\mathcal L}_{{\vec{\textbf{a}}}_3}(j) \equiv \left(\frac{1}{5}, \frac{1}{5} \right), \quad j \ge 1. \end{align*} $$

The second condition can be easily verified, and we would like to leave the detail to the interested reader.

Part 2. A geometric approach

In the second part of this paper, we provide an alternative way, based on the underlying geometry of n-adic systems, to generalize the one-dimensional result Theorem 2.2. This approach is much more intuitive and unifies the proof of both the cases $d=1$ and $d>1$ .

6 Notations

For $A, B \subset \mathbb {R}^d$ , we write the distance between them by

$$ \begin{align*}\textrm{dist}(A, B):=\inf_{x \in A, y \in B} \|x-y\|_{\mathbb{R}^d}. \end{align*} $$

Definition 6.1 Let $x \in \mathbb {R}^d$ and $A \subseteq \mathbb {R}^d$ , and the natural deviation between x and A is defined to be

$$ \begin{align*}\textrm{dev}(A, x):=\max_{1 \le k \le d} \textrm{dist}_{\vec{e}_k} (A, x), \end{align*} $$

where $\textrm {dist}_{\vec {e}_k}(A, x)$ denotes the distance between x and A along the direction $\vec {e}_k$ .

Remark 6.2 Let us make some remarks for the above definition.

1. (1) The word “natural” refers to the fact that we take the natural basis

   $$ \begin{align*}\{\vec{e}_1, \dots, \vec{e}_d\} \end{align*} $$
   in the definition. In general, one can replace $\{\vec {e}_1, \dots , \vec {e}_d\}$ by any other basis in $\mathbb {R}^d$ ; however, it is enough to take the natural basis in this paper.

2. (2) The word “deviation” refers to the fact that we take the maximal directional distance along all the directions $\vec {e}_1, \dots , \vec {e}_d$ .

3. (3) In our application later, A will be either a corner set (see Definition 7.1), a modulated corner set (see Definition 7.17), or a union of them.

Let us include an easy example for these definitions (see Figure 2). In this example, we consider the case $d=2$ , x is the point $\left (\frac {1}{2}, \frac {3}{10} \right )$ , and A is the red part (which we will refer as a corner set later). Then it is clear that

$$ \begin{align*}\text{dist}(x, A)=\frac{3}{10}-\frac{1}{10}=\frac{1}{5} \quad \textrm{and} \quad \text{dev}(x, A)=\frac{1}{2}-\frac{1}{6}=\frac{1}{3}. \end{align*} $$

Figure 2: Distance and natural deviation.

We frequently use the terms offspring and ancestor to refer to the generations of a given dyadic cube. In particular, we often use the letter m to refer to any generation (that is both offspring and ancestor) while the letter j is specifically reserved for ancestors. This use comes from the roles of m and j in the shift and location, parameters described below.

7 Fundamental structures of $d+1\ n$ -adic systems in $\mathbb {R}^d$

In this section, we introduce several basic structures of a collection of $d+1\ n$ -adic systems, where we recall that $d+1$ is optimal in the sense that any $d\ n$ -adic systems in $\mathbb {R}^d$ are not adjacent, while there exists a collection of $d+1\ n$ -adic grids, which are adjacent. Using these basic structures, we are able to generalize Theorem 2.2 to higher dimensions in a natural way.

This section consists of three parts, which are the all generations case, the small-scale case, and the large-scale case. Here, the word “small scale” refers to all the offspring generations of the zeroth generation, whereas the word “large scale” refers to all the ancestor generations of the zeroth generation, together with itself. Moreover, we also introduce the concept of n-far vector, which generalize the early definition of n-far number in one-dimensional case (see Definition 2.1). Finally, there are also many concrete examples given for the purpose of understanding these structures better.

Here is a list on all the structures that we are going to introduce in this section.

• • All generations case (Section 7.1): Corner sets (see Definition 7.1);

• • Small-scale case (Section 7.2): Small-scale lattice (see Definition 7.5) and n-far vectors (see Definition 7.9);

• • Large-scale case (Section 7.3): Large-scale sampling (see Definition 7.12), Large-scale lattice (see Definition 7.14), and Modulated corner sets (see Definition 7.17).

7.1 Corner sets

In the first part of this section, let us introduce an important structure for ${\mathcal G}(\delta , {\mathcal L}_{{\vec {\textbf {a}}}})$ , which can be viewed as a “generator” of ${\mathcal G}(\delta , {\mathcal L}_{{\vec {\textbf {a}}}})$ .

Definition 7.1 Let ${\mathcal G}(\delta , {\mathcal L}_{{\vec {\textbf {a}}}})$ be an n-adic grid in $\mathbb {R}^d$ . For $\ell \in \mathbb {Z}$ , we define the $\ell $ th corner operation

$$ \begin{align*}{\mathcal C}_{{\vec{\textbf{a}}}}^{\delta}(\ell) :{\mathcal A}(\delta, {\mathcal L}_{{\vec{\textbf{a}}}})_{\ell} \to \mathbb{R}^d \end{align*} $$

is given by

$$ \begin{align*}\left[{\mathcal C}_{{\vec{\textbf{a}}}}^{\delta}(\ell)\right] (x):= \bigcup_{i=1}^d \prod_i \left(x, \left[(x)_1, (x)_1+n^{-\ell} \right) \times \left[(x)_d, (x)_d+n^{-\ell} \right) \right), \end{align*} $$

where for any $x \in \mathbb {R}^d$ and $A \subset \mathbb {R}^d$ , $\prod _i(x, A)$ denotes the projection of A to the hyperplane $\{y \in \mathbb {R}^d: (y)_i=(x)_i \}$ . We call the collection $\left [{\mathcal C}_{{\vec {\textbf {a}}}}^{\delta }(\ell )\right ] (x)$ the $\ell $ th corner set associated to x with parameters $(\delta , {\vec {\textbf {a}}})$ , and we refer x as the corner of the corner set $\left [{\mathcal C}_{{\vec {\textbf {a}}}}^{\delta } \right ](x)$ .

Below is an example of a corner set with its corner $x = \left (\frac {1}{3}, \frac {1}{3} \right )$ when $d=2, n=2$ , and $\ell =1$ (see Figure 3).

Figure 3: Corner and corner set.

7.2 Small-scale lattices and $n$ -far vectors

The goal of the second part of section is to generalize the concept of far numbers in one dimension to higher dimension. It turns out that the correct thing to do is looking at the so-called small-scale lattices with respect to d many vectors in $\mathbb {R}^d$ . We point out that such a construction is implicitly mentioned in Conde Alonso’s proof of showing that d grids are never adjacent [5].

Definition 7.2 Let $\delta \in \mathbb {R}^d$ , and we say $\delta $ is of unit size if $(\delta )_i \in [0, 1)$ for each $i \in \{1, \dots , d\}$ .

Let us first state an easy fact for the adjacent n-adic systems.

Lemma 7.3 Let ${\mathcal G}_1, \dots , {\mathcal G}_{d+1}$ be adjacent, with each of them having a representation

$$ \begin{align*}{\mathcal G}_i={\mathcal G}(\delta_i, {\mathcal L}_{{\vec{\textbf{a}}}_i}), \quad 1 \le i \le d+1. \end{align*} $$

Then, for each $k \in \{1, \dots , d\}$ ,

$$ \begin{align*}(\delta_i)_k \not\equiv (\delta_j)_k \quad (\mathrm{mod} \ 1), \quad 1 \le i \neq j \le d+1. \end{align*} $$

Proof To start with, we may assume that all $\delta _i$ ’s are of unit size. Otherwise, we consider $\delta _i':=\delta _i \quad (\textrm {mod} \ 1)$ , where the modulus $1$ is taken over all the coordinate components.

We prove it by contradiction. Without loss of generality, we may assume

$$ \begin{align*}A:=(\delta_1)_1=(\delta_2)_1. \end{align*} $$

This implies that

$$ \begin{align*}\left\{ x \in \mathbb{R}^d: x_1=A \right\} \subset b{\mathcal G}_{1, 0} \cap b{\mathcal G}_{2, 0}, \end{align*} $$

where $b{\mathcal G}_{1, 0}$ means the boundary of all cubes in the zeroth generation of ${\mathcal G}_1$ . This further shows that for any $m \ge 0$ , the set

$$ \begin{align*}\bigcap_{i=1}^{d+1} b{\mathcal G}_{i, m} \quad \textrm{is not empty.} \end{align*} $$

Indeed, it suffices to show that

(7.1) $$ \begin{align} \bigcap_{i=1}^{d+1} b{\mathcal G}_{i, 0} \quad \textrm{is not empty,} \end{align} $$

since

$$ \begin{align*}\bigcap_{i=1}^{d+1} b{\mathcal G}_{i, 0} \subset \bigcap_{i=1}^{d+1} b{\mathcal G}_{i, m} \end{align*} $$

for all $m \ge 0$ . While for a proof of (7.1), it suffices to note that the set

$$ \begin{align*}\left\{x \in \mathbb{R}^d: x_1=A, x_2=(\delta_3)_2, \dots, x_d=(\delta_{d+1})_d \right\} \subset \bigcap_{i=1}^{d+1} b{\mathcal G}_{i, 0}. \end{align*} $$

To complete the proof, it suffices to follow Conde Alonso’s argument. Namely, we pick a point $a \in \bigcap \limits _{i=1}^{d+1} b{\mathcal G}_{i, 0}$ and we take a small cube centered at a. It is clear that the only way to cover this ball by using the cubes from $\bigcup \limits _{i=1}^{d+1} {\mathcal G}_i$ is to use a cube whose sidelength is at least n. Shrinking the sidelength of the cube as small as we want, this gives a contradiction to the second property in Definition 1.3.

Therefore, this easy lemma suggests the following definition.

Definition 7.4 Given $\delta _1, \dots , \delta _\ell \in \mathbb {R}^d$ , where $\ell \ge 1, \ell \in \mathbb {Z}$ , we say that they are separated if

$$ \begin{align*}(\delta_i)_k \neq (\delta_j)_k \quad (\textrm{mod} \ 1), \end{align*} $$

for all $k \in \{1, \dots , d\}$ and $1 \le i \neq j \le \ell $ .

Now, we are ready to introduce the so-called small-scale lattices.

Definition 7.5 Let $m \ge 0$ and $\delta _1, \dots , \delta _d \in \mathbb {R}^d$ be separated. Then the small-scale lattice associated to $\delta _1, \dots , \delta _d$ at level m is defined as

$$ \begin{align*}{\mathfrak L}(\delta_1, \dots, \delta_d; m):=\bigcap_{i=1}^d b\left[{\mathcal G}(\delta_i)_m\right], \end{align*} $$

where ${\mathcal G}(\delta )_m$ is defined as in Definition 3.1 and $b\left [{\mathcal G}(\delta )_m\right ]$ refers to the union of all the boundary of the cubes in ${\mathcal G}(\delta )_m$ .

Example 7.6 Let us give an example of such a structure (see Figure 4), in which we consider the set ${\mathcal L}\left ( \left (\frac {1}{3}, \frac {1}{3}\right ), \left (\frac {2}{3}, \frac {2}{3}\right ); 1 \right )$ with $d=2$ and $n=2$ . More precisely, in Figure 4, the red dashed lattice represents $b \left [{\mathcal G} \left ( \left (\frac {1}{3}, \frac {1}{3} \right ) \right )_1 \right ]$ , the blue dashed lattice represents $b \left [{\mathcal G} \left ( \left (\frac {2}{3}, \frac {2}{3} \right ) \right )_1 \right ]$ , and the collection of all green points stands for ${\mathcal L}\left ( \left (\frac {1}{3}, \frac {1}{3}\right ), \left (\frac {2}{3}, \frac {2}{3}\right ); 1 \right )$ .

Figure 4: ${\mathcal L}\left ( \left (\frac {1}{3}, \frac {1}{3}\right ), \left (\frac {2}{3}, \frac {2}{3}\right ); 1 \right )$ .

Remark 7.7

1. (1) We call it “small scale,” in the sense that set ${\mathfrak L}(\delta _1, \dots , \delta _d; m)$ is constructed with respect to the boundary of cubes of small sidelength.

2. (2) Since $\delta _1, \dots , \delta _d$ are separated, ${\mathfrak L}(\delta _1, \dots , \delta _d; m)$ is countable (it contains no lines).

3. (3) ${\mathfrak L}(\delta _1, \dots , \delta _d; m) \subset {\mathfrak L}(\delta _1, \dots , \delta _d; m')$ for all $m' \ge m$ .

There is an equivalent way to define ${\mathcal L}(\delta _1, \dots , \delta _d; m)$ .

Lemma 7.8 Let $\delta _1, \dots , \delta _d$ be separated. For each $\sigma \in S_d$ , where $S_d$ refers to the finite symmetric group over $\{1, \dots , d\}$ , denote

$$ \begin{align*}\delta_\sigma:=\left( \left(\delta_{\sigma(1)} \right)_1, \dots, \left(\delta_{\sigma(d)} \right)_d \right) \in \mathbb{R}^d. \end{align*} $$

Then, for each $m \ge 0$ , there holds

$$ \begin{align*}{\mathcal L}(\delta_1, \dots, \delta_d; m)=\bigcup_{\sigma \in S_d} {\mathcal A}(\delta_\sigma)_m. \end{align*} $$

Proof The desired result follows from the observation that $\delta _\sigma \in {\mathcal L}(\delta _1, \dots , \delta _d; m)$ and hence ${\mathcal A}(\delta _\sigma )_m \subset {\mathcal L}(\delta _1, \dots , \delta _d; m)$ . One may consult Figure 4 for an example of such a fact.

Let us denote

$$ \begin{align*}{\mathfrak L}(\delta_1, \dots, \delta_d):=\bigcup_{m \ge 0} {\mathfrak L}(\delta_1, \dots, \delta_d; m) \end{align*} $$

be the union of all small-scale lattices.

We are ready to generalize the concept of far number in dimension-one case.

Definition 7.9 Given $\delta _1, \dots , \delta _d \in \mathbb {R}^d$ being separated, we say $\delta \in \mathbb {R}^d$ is an n-far vector with respect to ${\mathfrak L}(\delta _1, \dots , \delta _d)$ , if there exists some $C>0$ , such that for every $m \ge 0$ , there holds

(7.2) $$ \begin{align} \textrm{dist} \left(b\left[{\mathcal G}(\delta)_m\right], {\mathfrak L}(\delta_1, \dots, \delta_d; m) \right) \ge \frac{C}{n^m}. \end{align} $$

Remark 7.10 While the above definition looks quite different from Definition 1.3 of [2], we can actually motivate our definition from [2]. In the one-dimensional case, the set $\{\delta _1, \dots , \delta _d\}$ reduces to the set $\{0\}$ . Therefore, n-far in the one-dimensional case reduced to checking that

(7.3) $$ \begin{align} \left|\delta-\frac{k}{n^m} \right| \ge \frac{C}{n^m}, \end{align} $$

for $k \in \mathbb {Z}$ and $m \ge 0$ (see Remark 1.4(2) in [2]). Due to such a simple structure, Theorem 2.8 in [2] asserted that $\delta \in \mathbb {R}$ is n-far if and only if the maximal length of tie, that is, the maximal length of consecutive $0$ ’s or consecutive ( $n-1$ )’s in the base n-representation of $\delta $ , is finite.

The key point to generalize the concept of n-far number in higher dimension is to realize that $\delta $ and $\frac {k}{n^m}$ are indeed playing different roles in condition (7.3). More precisely, rewrite (7.3) as

$$ \begin{align*}\left| \left(\delta-\frac{k_1}{n^m} \right)-\frac{k_2}{n^m} \right| \ge \frac{C}{n^m} \end{align*} $$

for $k_1, k_2 \in \mathbb {Z}$ and $m \ge 0$ . Here are the key observations: let $m \ge 0$ be fixed, then:

1. (1) when $k_1$ varies, the set

   $$ \begin{align*}\left\{ \delta-\frac{k_1}{n^m}: k_1 \in \mathbb{Z} \right\} \end{align*} $$
   represents the all the boundary points $b\left [{\mathcal G}(\delta )_m \right ]$ ;

2. (2) when $k_2$ varies, the set

   $$ \begin{align*}\left\{\frac{k_2}{n^m}: k_2 \in \mathbb{Z} \right\} \end{align*} $$
   represents the small-scale lattice ${\mathcal L}(0; m)$ . This is clear from Lemma 7.8.

Hence, an equivalent way to state (7.3) is the following: for any $m \ge 0$ ,

$$ \begin{align*}\textrm{dist} \left( b\left[ {\mathcal G}(\delta)_m \right], {\mathcal L}(0; m) \right) \ge \frac{C}{n^m}, \end{align*} $$

which is precisely (7.2). The key here is that the boundary points and the small-scale lattice align in dimension 1.

Example 7.11 We now illustrate via an example why the idea of generalizing the concept of far numbers to pairwise distances is not sufficient to show that $d+1$ grids are adjacent. Take $\delta _1 = (0,0), \delta _2 = \left (0,\frac {1}{3}, \right )$ and $\delta _3 = \left (\frac {1}{3},\frac {1}{3} \right )$ . Consider the natural pairwise generalization of far where $\delta $ and $\delta '$ are far if $(\delta )_i$ is far from $(\delta ')_i$ for some i. Using this definition, we see that each of these points is far from each other, but $\delta _1, \delta _2, \delta _3$ do no form an adjacent n-adic system. In fact, if one looks at $\mathcal {L}(\delta _1, \delta _2;0)$ , one does not get a lattice, but a set of vertical lines (see Figure 5).

Figure 5: A nonexample of small-scale lattice: $b[{\mathcal G}(\delta _1)]_0$ (black part), $b[{\mathcal G}(\delta _2)]_0$ (blue part), $b[{\mathcal G}(\delta _3)]_0$ (red part), and the nonexample $b\left [{\mathcal G}(\delta _1)\right ]_0 \cap b\left [{\mathcal G}(\delta _2)\right ]_0$ (green part).

Therefore, this pairwise comparison between points is not enough to determine an adjacent n-adic system and the lattice structure is needed.

7.3 Large-scale sampling, large-scale lattice, and modulated corner sets

The purpose of the last part of section is to introduce all the basic structures with respect to d separated vectors and d location functions, which is used to study the large-scale case. Informally, these structures are the counterparts of the small-scale lattice (see Definition 7.5) and the usual corner sets (see Definition 7.1); however, one new phenomenon for the large scale is that one needs to use the cube $[0, n^j)^d$ to quantify the behavior of the location function (see Theorem 8.1(ii)), and this suggests that we need a localized version of those structures in the large-scale case.

The setting is as follows. Let $\delta _1, \dots , \delta _d \in \mathbb {R}^d$ be separated, ${\vec {\textbf {a}}}_1, \dots , {\vec {\textbf {a}}}_d$ be the d many infinite matrices defined in (3.1), and ${\mathcal L}_{{\vec {\textbf {a}}}_1}, \dots , {\mathcal L}_{{\vec {\textbf {a}}}_d}$ be the corresponding location functions.

Definition 7.12 For each $j>0$ , the large-scale sampling associated to the tuples

$$ \begin{align*}\left(\delta_1, {\vec{\textbf{a}}}_1\right), \dots, \left(\delta_d, {\vec{\textbf{a}}}_d\right) \end{align*} $$

at level j is defined by

$$ \begin{align*}{\mathcal S}_{{\vec{\textbf{a}}}_1, \dots, {\vec{\textbf{a}}}_d}^{\delta_1, \dots, \delta_d}(j):=\left( \bigcap_{k=1}^d b\left[ {\mathcal G}(\delta_k, {\mathcal L}_{{\vec{\textbf{a}}}_k})_{-j}\right]\right) \cap [0, n^j)^d. \end{align*} $$

Example 7.13 Let $d=2, n=2$ , $\delta _1 = \left (\frac {1}{3}, \frac {1}{3} \right )$ , and $\delta _2 = \left (\frac {2}{3}, \frac {2}{3} \right )$ . We illustrate below the large-scale sampling (see Figure 6) for $j=1$ for $\left (\delta _1, {\vec {\textbf {a}}}_1 \right )$ and $\left (\delta _2, {\vec {\textbf {a}}}_2 \right )$ (in the cube $[0,2)^2)$ ) in Figure 6, where

$$ \begin{align*}{\vec{\textbf{a}}}_1:= \begin{pmatrix} 1 & 0 & 1 & 0 & \dots\\ 1 & 0 & 1 & 0 & \dots \end{pmatrix} \end{align*} $$

and

$$ \begin{align*}{\vec{\textbf{a}}}_2:=\begin{pmatrix} 0 & 1 & 0 & 1 & \dots\\ 0 & 1 & 0 & 1 & \dots \end{pmatrix} \end{align*} $$

Figure 6: An example of large-scale sampling: $A=\delta _1+{\mathcal L}_{ {\vec {\textbf {a}}}_1}(1)=\left (\frac {4}{3}, \frac {4}{3} \right )$ , $B=\delta _2+{\mathcal L}_{{\vec {\textbf {a}}}_2}(1)=\left (\frac {2}{3}, \frac {2}{3} \right )$ , $b\left [{\mathcal G}(\delta _1, {\vec {\textbf {a}}}_1) \right ]_{-1}$ (red part), $b\left [{\mathcal G}(\delta _2, {\vec {\textbf {a}}}_2) \right ]_{-1}$ (blue part), and the large-scale sampling ${\mathcal S}_{{\vec {\textbf {a}}}_1, {\vec {\textbf {a}}}_2}^{\delta _1, \delta _2}(1)$ (green part).

Let us extend the definition of small-scale lattice to the large scales, which can be viewed as a “global” version of the large-scale sampling.

Definition 7.14 For each $m<0$ , the large-scale lattice associated to the tuples

$$ \begin{align*}\left(\delta_1, {\vec{\textbf{a}}}_1\right), \dots, \left(\delta_d, {\vec{\textbf{a}}}_d\right) \end{align*} $$

at level m is defined by

$$ \begin{align*}{\mathcal L}_{{\vec{\textbf{a}}}_1, \dots, {\vec{\textbf{a}}}_d}^{\delta_1, \dots, \delta_d}(m):=\bigcap_{k=1}^d b\left[ {\mathcal G}(\delta_k, {\mathcal L}_{{\vec{\textbf{a}}}_k})_m\right]. \end{align*} $$

Remark 7.15 Again, we emphasize the use of $j=-m$ where $m<0$ and j refers to the jth ancestor (that is, the $-j$ th generation in Definition 3.1). We only use this identification for the large cubes; the reason we do so is to be consistent with the terminology in [2].

Remark 7.16

1. 1. Note that since $\delta _1, \dots , \delta _d$ are assumed to be separated, ${\mathcal S}_{{\vec {\textbf {a}}}_1, \dots , {\vec {\textbf {a}}}_d}^{\delta _1, \dots , \delta _d}(j)$ is a finite set, whereas ${\mathcal L}_{{\vec {\textbf {a}}}_1, \dots , {\vec {\textbf {a}}}_d}^{\delta _1, \dots , \delta _d}(m)$ is countable.

2. 2. The reason for us to start with a negative m in the definition of large-scale lattice is to keep the consistency with the definition of small-scale lattice.

3. 3. The large-scale sampling can be viewed as a “generator” of the large-scale lattice. More precisely, we have, for each $m>0$ , there holds

   $$ \begin{align*}{\mathcal L}_{{\vec{\textbf{a}}}_1, \dots, {\vec{\textbf{a}}}_d}^{\delta_1, \dots, \delta_d}(m)=\bigcup_{p \in \mathbb{Z}^d} \left({\mathcal S}_{{\vec{\textbf{a}}}_1, \dots, {\vec{\textbf{a}}}_d}^{\delta_1, \dots, \delta_d}(-m)+n^j p\right). \end{align*} $$

We need one more definition to state our main result in large scale.

Definition 7.17 Let $j \ge 0$ , $\delta \in \mathbb {R}^d$ , ${\vec {\textbf {a}}}$ be an infinite matrix defined in (3.1), and ${\mathcal L}_{{\vec {\textbf {a}}}}$ be the associated location function. Then the jth modulated corner set associated to $(\delta , {\vec {\textbf {a}}})$ is defined to be

$$ \begin{align*}(m{\mathcal C})_{{\vec{\textbf{a}}}}^{\delta}(j):=\left( b \left[{\mathcal G}(\delta, {\mathcal L}_{\vec{\textbf{a}}}) \right]_{-j}\right) \cap [0, n^j)^d. \end{align*} $$

Example 7.18 We give an easy example of such a structure (see Figure 7). Here, we take our favorite example, that is, we consider the case when $d=2$ , $n=2, j=1$ , $\delta =\left (\frac {1}{3}, \frac {1}{3} \right )$ , and ${\vec {\textbf {a}}}:= \begin {pmatrix} 1 & 0 & 1 & 0 & \dots \\ 1 & 0 & 1 & 0 & \dots \end {pmatrix}$ .

Figure 7: $(m{\mathcal C})_{{\vec {\textbf {a}}}}^{\left (\frac {1}{3}, \frac {1}{3} \right )}(1)$ .

Remark 7.19

1. 1. A trivial observation would be for any $y' \in {\mathcal S}_{{\vec {\textbf {a}}}_1, \dots , {\vec {\textbf {a}}}_d}^{\delta _1, \dots , \delta _d}(j)$ , there holds

   $$ \begin{align*}0 \le \frac{\textrm{dev} \left( (m {\mathcal C})_{\vec{\textbf{a}}}^{\delta}(j), y' \right)}{n^j}<1. \end{align*} $$

2. 2. The corner sets and modulated corner sets are closely related. More precisely, we have, for any $d \ge 1$ and $j \ge 0$ , there holds

   $$ \begin{align*}\left[{\mathcal C}_{{\vec{\textbf{a}}}}^{\delta}(-j) \right] \left(\delta+{\mathcal L}_{{\vec{\textbf{a}}}}(j) \quad (\textrm{mod} \ n^j) \right) \equiv (m{\mathcal C})_{{\vec{\textbf{a}}}}^{\delta}(j) \quad (\textrm{mod} \ n^j). \end{align*} $$

In our later application, the modulated corner sets will only be applied to study the ancestors of the zeroth generation, whereas the corner sets defined early will take care of all the generations. More precisely, the modulated corners are important to take care of points near the boundary of the cube $[0, n^j)^d$ that might be close to a corner lying just outside $[0,n^j)^d$ but far from the modulated corner. This remark will be made clearer in the next section and indeed underlies our use of modulated corners.

8 An alternative approach

Let us go back to the main question that we are interested in, namely, what the necessary and sufficient conditions are, so that a given collection of $d+1\ n$ -adic grids are adjacent?

The goal of this section is to provide an alternative way to answer the above question via the fundamental structures, and to comment about the uniformity of such a representation. To begin, let us write these $d+1\ n$ -adic grids by their representations, namely ${\mathcal G}(\delta _1, {\mathcal L}_{{\vec {\textbf {a}}}_1}), \dots , {\mathcal G}(\delta _{d+1}, {\mathcal L}_{{\vec {\textbf {a}}}_{d+1}})$ . Moreover, using Lemma 7.3, we may assume $\delta _1, \dots , \delta _{d+1}$ are separated.

8.1 Motivation and the structure theorem of adjacency

As mentioned in the introduction, the intuition behind the next theorem originates back to the one-dimensional result (see Theorem 2.2). The main idea to generalize the first condition is already contained in Remark 7.10. More precisely, we can rewrite condition (1) as: there exists some absolute constant $C>0$ , such that for any $k_1, k_2 \in \mathbb {Z}$ and $m \ge 0$ , it holds that

$$ \begin{align*}\left| \left( \delta_1-\frac{k_1}{n^m} \right)-\left( \delta_2-\frac{k_2}{n^m} \right) \right| \ge \frac{C}{n^m}. \end{align*} $$

For simplicity, we may assume both $\delta _1, \delta _2 \in [0, 1)$ , that is, both of them are of unit size (although we do not require such a restriction in our main result). As in Remark 7.10, there are two different ways to interpret the sets

$$ \begin{align*}\left\{\delta_i-\frac{k}{n^m}: k_i \in \mathbb{Z} \right\}, \quad i=1, 2. \end{align*} $$

The first way is to interpret each set as the set of all the boundary points $b\left [ {\mathcal G}(\delta _i)_m\right ]$ , whereas the second way is to treat it as the small-scale lattice ${\mathfrak L}(\delta _i; m)$ . Therefore, we can restate the first condition as

$$ \begin{align*} \delta_1\ \mathit{is}\ n-\mathit{far}\ \mathit{with}\ \mathit{respect}\ \mathit{to}\ {\mathfrak L}(\delta_2)\ \mathit{and}\ \delta_2\ \mathit{is}\ n-far\ \mathit{with}\ \mathit{respect}\ \mathit{to}\ {\mathfrak L}(\delta_1). \end{align*} $$

While for condition (2), note that it is equivalent to the following:

(8.1) $$ \begin{align} 0<\liminf_{j \to \infty} \left| \frac{\delta_1+{\mathcal L}_{{\vec{\textbf{a}}}_1}(j)-\delta_2-{\mathcal L}_{{\vec{\textbf{a}}}_2}(j)}{n^j} \right| \le \limsup_{j \to \infty} \left| \frac{\delta_1+{\mathcal L}_{{\vec{\textbf{a}}}_1}(j)-\delta_2-{\mathcal L}_{{\vec{\textbf{a}}}_2}(j)}{n^j} \right|<1. \end{align} $$

Similarly, there are two ways to interpret the sets (which contain only one element in the one-dimensional case):

(8.2) $$ \begin{align} \left\{ \delta_i+{\mathcal L}_{{\vec{\textbf{a}}}_i}(j) \right\}, \quad i=1, 2, \end{align} $$

for any $j \ge 1$ . The first way is to regard each as a jth modulated corner set, namely, $(m{\mathcal C})_{{\vec {\textbf {a}}}_i}^{\delta _i}(j)$ , whereas the second way is to consider it as a large-scale sampling at level j, that is, ${\mathcal S}_{{\vec {\textbf {a}}}_i}^{\delta _i}(j)$ . If one sets the interpretation of the first set as the modulated corner and of the second set as the large-scale sampling, then additionally there are also two different ways to understand the term

(8.3) $$ \begin{align} \left| \delta_1+{\mathcal L}_{{\vec{\textbf{a}}}_1}(j)-\delta_2-{\mathcal L}_{{\vec{\textbf{a}}}_2}(j) \right|. \end{align} $$

The first way is to treat it as

$$ \begin{align*}\textrm{dist} \left( (m{\mathcal C})_{{\vec{\textbf{a}}}_i}^{\delta_i}(j), {\mathcal S}_{{\vec{\textbf{a}}}_{i'}}^{\delta_{i'}}(j) \right), \end{align*} $$

where $\{i, i'\}=\{1, 2\}$ , whereas the second way is to regard it as the “maximum distance” between these two sets, that is,

$$ \begin{align*}\max_{y' \in {\mathcal S}_{{\vec{\textbf{a}}}_{i'}}^{\delta_{i'}}(j)} \textrm{dev} \left( (m{\mathcal C})_{{\vec{\textbf{a}}}_i}^{\delta_i}(j), y' \right). \end{align*} $$

Note that all these complicated structures (that is, the modulated corner set and large-scale sampling) collapse into a single point in the one-dimensional case, and all those quantities coincide with each other and take the value (8.3); however, in higher dimension, we need to treat them differently.

Here is the main result for the second part, which can be thought as some structure theorem of adjacency with respect to a collection of $d+1\ n$ -adic grids.

Theorem 8.1 The collection of n-adic grids ${\mathcal G}(\delta _1, {\mathcal L}_{{\vec {\textbf {a}}}_1}), \dots , {\mathcal G}(\delta _{d+1}, {\mathcal L}_{{\vec {\textbf {a}}}_{d+1}})$ are adjacent if and only if:

1. (i) For each $i \in \{1, \dots , d+1\}$ , $\delta _i $ is n-far with respect to ${\mathfrak L}\left (\delta _1, \dots , \widehat {\delta _i}, \dots , \delta _{d+1}\right )$ . Here, $\widehat {\delta _i}$ means that in the sequence $\{\delta _1, \dots , \delta _{d+1}\}$ , we remove the term $\delta _i$ .

2. (ii) For each $i \in \{1, \dots , d+1\}$ , there holds

   (8.4) $$ \begin{align} 0&<\liminf_{j \to \infty} \frac{\textrm{dist} \left( (m{\mathcal C})_{{\vec{\textbf{a}}}_i}^{\delta_i} (j), {\mathcal S}_{{\vec{\textbf{a}}}_1, \dots, \widehat{{\vec{\textbf{a}}}_i}, \dots, {\vec{\textbf{a}}}_{d+1}}^{\delta_1, \dots, \widehat{\delta_i}, \dots, \delta_{d+1}}(j) \right)}{n^j} \nonumber \\ & \le \limsup_{j \to \infty} \frac{\max_{y' \in {\mathcal S}_{{\vec{\textbf{a}}}_1, \dots, \widehat{{\vec{\textbf{a}}}_i}, \dots, {\vec{\textbf{a}}}_{d+1}}^{\delta_1, \dots, \widehat{\delta_i}, \dots, \delta_{d+1}}(j)} \textrm{dev}\left( (m{\mathcal C})_{{\vec{\textbf{a}}}_i}^{\delta_i} (j), y' \right)}{n^j} <1. \end{align} $$

Note that in the above statement, for each $j>0$ and $i \in \{1. \dots , d+1\}$ ,

$$ \begin{align*}{\mathcal S}_{{\vec{\textbf{a}}}_1, \dots, \widehat{{\vec{\textbf{a}}}_i}, \dots, {\vec{\textbf{a}}}_{d+1}}^{\delta_1, \dots, \widehat{\delta_i}, \dots, \delta_{d+1}}(j) \end{align*} $$

is a finite set, and hence the maximum value in the limit superior can be attained.

Remark 8.2 Note that the above result is independent of the choice of the representation of the n-grid and hence contains the uniformness result Theorem 2.4 as a particular case. The reason is that the structures that we are working with, that is, the collection of all the boundary points at certain generations, the small-scale lattices, the modulated corner sets, and the large-scale sampling, are independent of the choice of the representations, whereas for the term

$$ \begin{align*}\delta+{\mathcal L}_{{\vec{\textbf{a}}}}(j) \end{align*} $$

(see (8.2) and (8.1)) that we used in our one-dimensional result indeed depends on the particular choices of the representation; more precisely, it is possible for us to find two equivalent presentations ${\mathcal G}(\delta , {\mathcal L}_{{\vec {\textbf {a}}}})$ and ${\mathcal G}(\delta ', {\mathcal L}_{{\vec {\textbf {a}}}'})$ such that

$$ \begin{align*}\delta+{\mathcal L}_{{\vec{\textbf{a}}}}(j)<n^j \le \delta'+{\mathcal L}_{{\vec{\textbf{a}}}'}(j) \end{align*} $$

for j sufficiently large. In such a situation, Theorem 8.1 suggests us to work with the point $\delta '+{\mathcal L}_{{\vec {\textbf {a}}}'}(j)-n^j$ instead of $\delta '+{\mathcal L}_{{\vec {\textbf {a}}}'}(j)$ , and this will guarantee that there is only one limit infimum and one limit superior in (8.4), instead many of them.

Proof of Theorem 8.1 It turns out the conditions (i) and (ii) above are indeed equivalent to the conditions (1) and (2) in Theorem 1.5, which indeed suggests Theorem 8.1 is a much more natural statement to consider. We would like to leave the detail to the interested reader.

8.2 Example revisited

Let us use Theorem 8.1 to verify the adjacency of the dyadic grids considered in Section 5. We start by verifying Condition (i) in Theorem 8.1. This means we have to show:

1. (a) $\delta _1$ is $2$ -far with respect to ${\mathfrak L}\left (\delta _2, \delta _3\right )$ ;

2. (b) $\delta _2$ is $2$ -far with respect to ${\mathfrak L}\left (\delta _1, \delta _3\right )$ ;

3. (c) $\delta _3$ is $2$ -far with respect to ${\mathfrak L}\left (\delta _1, \delta _2\right )$ .

We will show (c). First, it is easy to see that $\{\delta _1, \delta _2, \delta _3\}$ are separated. Note that calculating the quantity (7.2) for $m=1$ reduces to calculating in a “local region” (see the cyan part in Figure 8), as both $b[{\mathcal G}(\delta _3)]_1$ and ${\mathfrak L}(\delta _1, \delta _2; 1)$ behave periodically. Therefore, we can see that

$$ \begin{align*}\textrm{dist} \left(b\left[{\mathcal G}(\delta_3)\right]_1, {\mathfrak L}(\delta_1,\delta_2; 1) \right) = \min\left\{\frac{1}{3}-\frac{1}{5}, \ \frac{1}{5}-\frac{1}{6} \right\} = \frac{1/15}{2}. \end{align*} $$

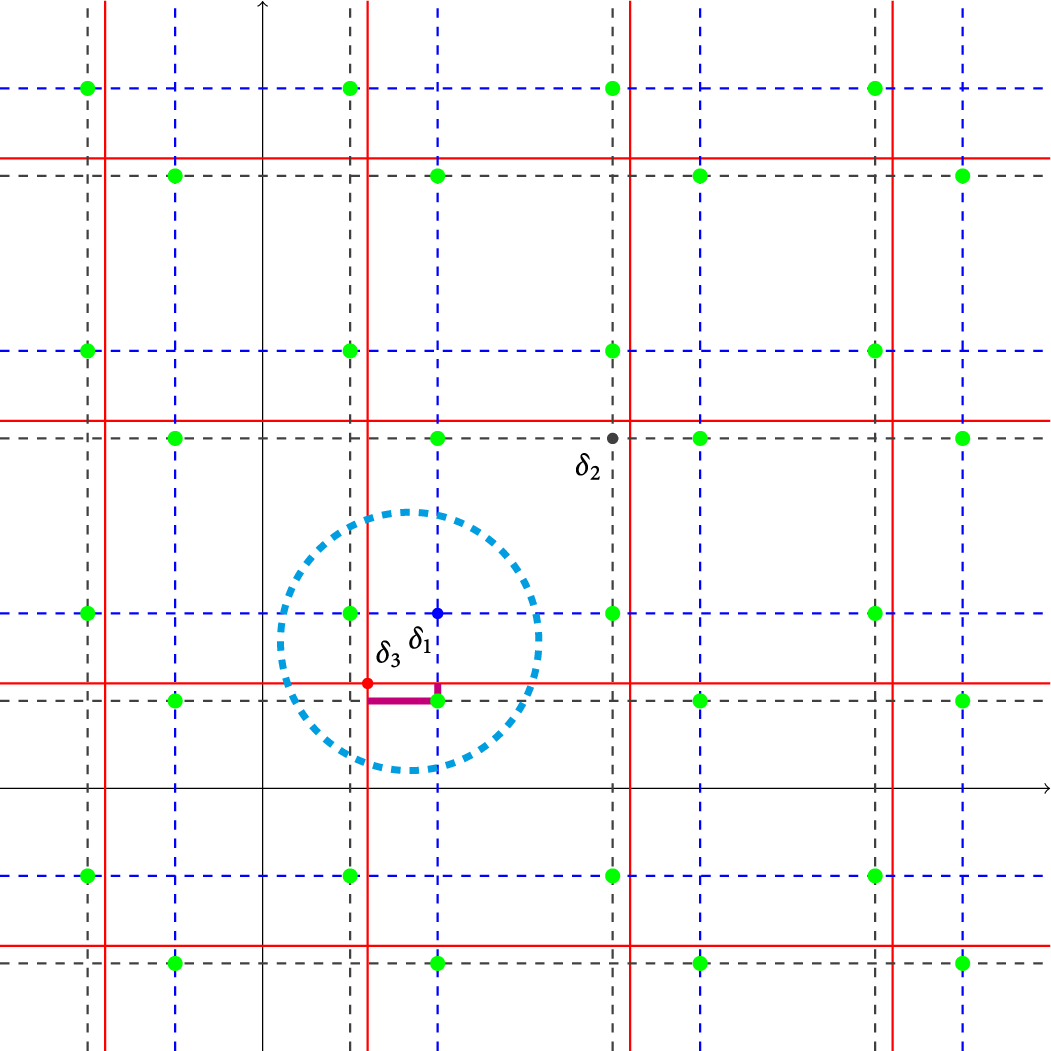
Figure 8: $b[{\mathcal G}(\delta _3)]_1$ (red part), the small-scale lattice ${\mathfrak L}(\delta _1, \delta _2; 1)$ (green part), the line segment with length $\frac {1}{3}-\frac {1}{5}=\frac {2}{15}$ (the horizontal magenta colored line), and the line segment with length $\frac {1}{5}-\frac {1}{6}=\frac {1}{30}$ (the vertical magenta colored line).

It turns out that this case $m=1$ already illustrates the main point. The case $m=0$ is even easier, and for all other $m>0$ , we will get either

$$ \begin{align*} \textrm{dist} \left(b\left[{\mathcal G}(\delta_3)\right]_m, {\mathfrak L}(\delta_1,\delta_2; m) \right) &= \inf_{k_1, k_2 \in \mathbb{Z}} \left|\left(\frac{1}{3} \pm \frac{k_1}{2^m} \right)- \left(\frac{1}{5} \pm \frac{k_2}{2^m} \right) \right| \\ &\geq \inf_{k_1, k_2 \in \mathbb{Z}} \left|\frac{2}{15} - \frac{k}{2^m} \right| \ge \frac{C}{2^m} \end{align*} $$

by techniques in [2, Proposition 2.4] (see also Lemma 3 in [1]), or a similar claim where $\frac {1}{3}$ is replaced by $\frac {2}{3}$ . The other calculations for (a) and (b) are similar. For example, by an easy modification of the above arguments, we have, for any $m \ge 0$ ,

$$ \begin{align*}\textrm{dist} \left(b\left[{\mathcal G}(\delta_1)\right]_m, {\mathfrak L}(\delta_2,\delta_3; m) \right) \end{align*} $$

(this is for (a)) is either

$$ \begin{align*}\inf_{k_1, k_2 \in \mathbb{Z}} \left|\left(\frac{2}{3} \pm \frac{k_1}{2^m} \right)- \left(\frac{1}{3} \pm \frac{k_2}{2^m} \right) \right| \end{align*} $$

or

$$ \begin{align*}\inf_{k_1, k_2 \in \mathbb{Z}} \left|\left(\frac{1}{5} \pm \frac{k_1}{2^m} \right)- \left(\frac{1}{3} \pm \frac{k_2}{2^m} \right) \right|, \end{align*} $$

which is clearly bounded below by some $\frac {C}{2^m}$ , where C is independent of the choice of m. We leave the details to the interested reader.

We now verify Condition (ii). We first calculate the limit infimum, and begin by examining the case $j=1$ . In this case, it is clear from Figure 9 that

$$\begin{align*}\frac{\textrm{dist} \left( (m{\mathcal C})_{{\vec{\textbf{a}}}_1}^{\delta_1} (1), {\mathcal S}_{{\vec{\textbf{a}}}_2, {\vec{\textbf{a}}}_{3}}^{\delta_2, \delta_{3}}(1) \right)}{2} = \frac{1}{3}, \end{align*}$$

whereas

$$\begin{align*}\frac{\textrm{dist} \left( (m{\mathcal C})_{{\vec{\textbf{a}}}_2}^{\delta_2} (1), {\mathcal S}_{{\vec{\textbf{a}}}_1, {\vec{\textbf{a}}}_{3}}^{\delta_1, \delta_{3}}(1) \right)}{2} = \frac{\textrm{dist} \left( (m{\mathcal C})_{{\vec{\textbf{a}}}_3}^{\delta_3} (1), {\mathcal S}_{{\vec{\textbf{a}}}_1, {\vec{\textbf{a}}}_{2}}^{\delta_1, \delta_{2}}(1) \right)}{2} = \frac{|2/3-1/5|}{2} =\frac{7}{15}. \end{align*}$$

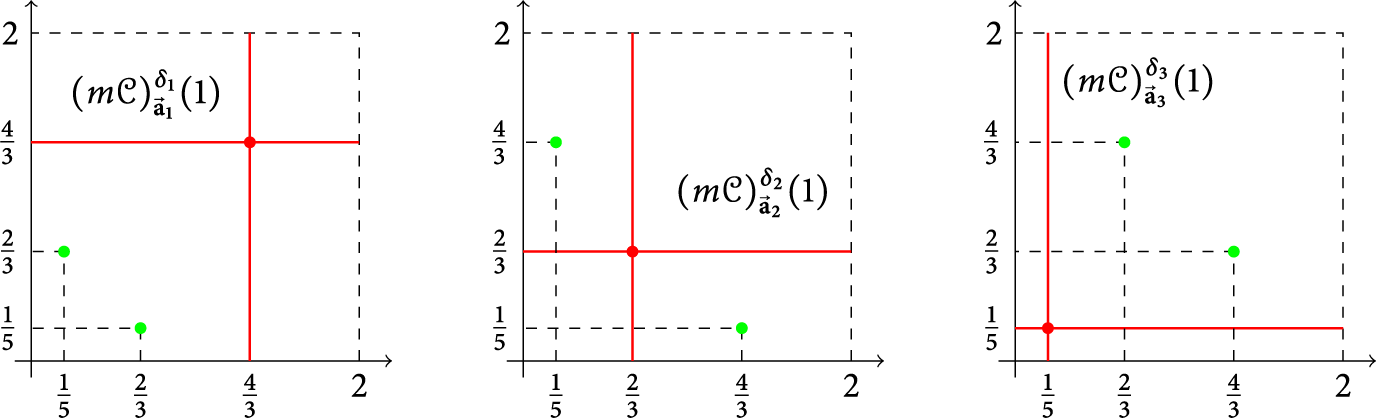
Figure 9: All modulated corner sets $(m{\mathcal C})_{{\vec {\textbf {a}}}_i}^{\delta _i}(1)$ for $i=1, 2, 3$ (red parts) and all corresponding large-scale samplings ${\mathcal S}_{{\vec {\textbf {a}}}_1, \dots , \widehat {{\vec {\textbf {a}}}_i}, \dots , {\vec {\textbf {a}}}_3}^{\delta _1, \dots , \widehat {\delta _i}, \dots , \delta _3}(1)$ for $i=1, 2, 3$ (green parts).

Let us also calculate the case when $j=2$ (see Figure 10). In this case, we have

$$\begin{align*}\frac{\textrm{dist} \left( (m{\mathcal C})_{{\vec{\textbf{a}}}_2}^{\delta_2} (2), {\mathcal S}_{{\vec{\textbf{a}}}_1, {\vec{\textbf{a}}}_{3}}^{\delta_2, \delta_{3}}(2) \right)}{4} = \frac{1}{3}, \end{align*}$$

whereas

$$\begin{align*}\frac{\textrm{dist} \left( (m{\mathcal C})_{{\vec{\textbf{a}}}_1}^{\delta_1} (2), {\mathcal S}_{{\vec{\textbf{a}}}_2, {\vec{\textbf{a}}}_{3}}^{\delta_2, \delta_{3}}(2) \right)}{4} = \frac{\textrm{dist} \left( (m{\mathcal C})_{{\vec{\textbf{a}}}_3}^{\delta_3} (2), {\mathcal S}_{{\vec{\textbf{a}}}_1, {\vec{\textbf{a}}}_{2}}^{\delta_1, \delta_{2}}(2) \right)}{4} = \frac{4/3-1/5}{2} =\frac{17}{60}. \end{align*}$$

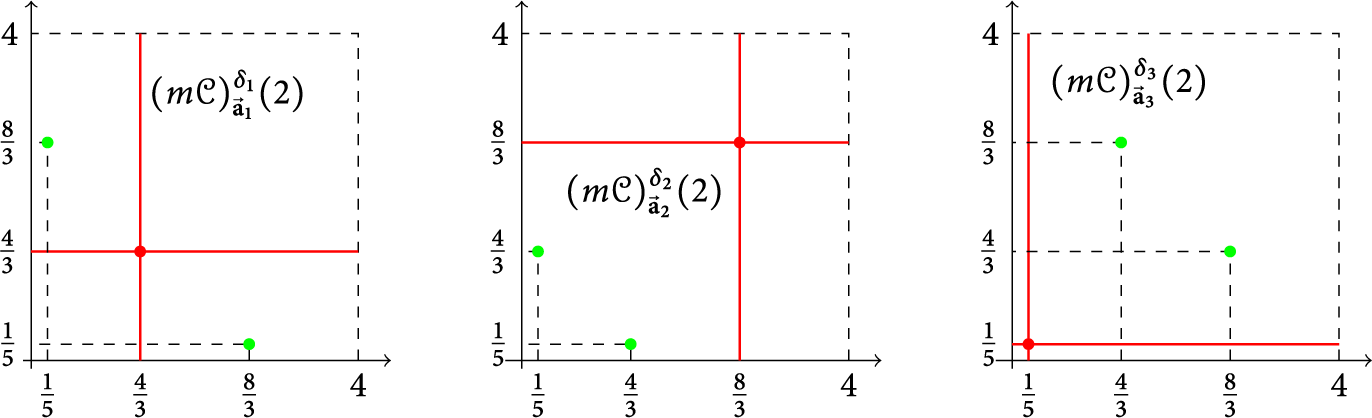
Figure 10: All modulated corner sets $(m{\mathcal C})_{{\vec {\textbf {a}}}_i}^{\delta _i}(2)$ for $i=1, 2, 3$ (red parts) and all corresponding large-scale samplings ${\mathcal S}_{{\vec {\textbf {a}}}_1, \dots , \widehat {{\vec {\textbf {a}}}_i}, \dots , {\vec {\textbf {a}}}_3}^{\delta _1, \dots , \widehat {\delta _i}, \dots , \delta _3}(2)$ for $i=1, 2, 3$ (green parts).

Similarly, the cases $j=1, 2$ (that is, $m=-1$ and $-2$ , respectively) contain all the main ideas for the large-scale case (that is, $m<0$ ). Recall that, for $j \ge 0$ ,

$$ \begin{align*}\delta_1+{\mathcal L}_{{\vec{\textbf{a}}}_1}(j)= \begin{cases} \left(\frac{2^{j}}{3}, \frac{2^{j}}{3} \right), & \hfill j \ \textrm{even}, \\ \\ \left(\frac{2^{j+1}}{3}, \frac{2^{j+1}}{3} \right), & \hfill j \ \textrm{odd}, \end{cases} \quad \delta_2+{\mathcal L}_{{\vec{\textbf{a}}}_2}(j)= \begin{cases} \left(\frac{2^{j+1}}{3}, \frac{2^{j+1}}{3} \right), & \hfill j \ \textrm{even}, \\ \\ \left(\frac{2^{j}}{3}, \frac{2^{j}}{3} \right), & \hfill j \ \textrm{odd}, \end{cases} \end{align*} $$

and

$$ \begin{align*}\delta_3+{\mathcal L}_{{\vec{\textbf{a}}}_3}(j) \equiv \left(\frac{1}{5}, \frac{1}{5} \right). \end{align*} $$

This suggests that the first two limit infimums, which are

$$ \begin{align*}\liminf_{j \to \infty} \frac{\textrm{dist} \left( (m{\mathcal C})_{{\vec{\textbf{a}}}_1}^{\delta_1} (j), {\mathcal S}_{{\vec{\textbf{a}}}_2, {\vec{\textbf{a}}}_{3}}^{\delta_2, \delta_{3}}(j) \right)}{2^j} \quad \textrm{and} \quad \liminf_{j \to \infty} \frac{\textrm{dist} \left( (m{\mathcal C})_{{\vec{\textbf{a}}}_2}^{\delta_2} (j), {\mathcal S}_{{\vec{\textbf{a}}}_1, {\vec{\textbf{a}}}_{3}}^{\delta_1, \delta_{3}}(j) \right)}{2^j}, \end{align*} $$

are either

$$ \begin{align*}\lim_{j \to \infty} \frac{2^{j+1}/3-2^j/3}{2^j}=\frac{1}{3} \end{align*} $$

or

$$ \begin{align*}\lim_{j \to \infty} \frac{2^j/3-1/5}{2^j}=\frac{1}{3}. \end{align*} $$

To see this, one may consider two different cases by requiring j being even or being odd, the desired claim will then follow from plotting the corresponding modulated corner sets and large-scale samplings out, as the first two graphs illustrated in Figure 9.

While for the third limit infimum, that is,

$$ \begin{align*}\liminf_{j \to \infty} \frac{\textrm{dist} \left( (m{\mathcal C})_{{\vec{\textbf{a}}}_3}^{\delta_3} (j), {\mathcal S}_{{\vec{\textbf{a}}}_1, {\vec{\textbf{a}}}_{2}}^{\delta_1, \delta_{2}}(j) \right)}{2^j}, \end{align*} $$

we can see that it will be

$$ \begin{align*}\lim_{j \to \infty} \frac{2^j/3-1/5}{2^j}=\frac{1}{3}. \end{align*} $$

One may consult the third graph in Figure 9 for a visualization of this case. Overall, we can take $\frac {1}{3}$ as the limit infimum in Condition (ii) of our main result.

The calculations for the limit supreme are similar and can be visualized from Figure 9. More precisely, we can see that the quantity

$$ \begin{align*}\max_{i=1,2,3} \left[\limsup_{j \to \infty} \frac{\max_{y' \in {\mathcal S}_{{\vec{\textbf{a}}}_1, \dots, \widehat{{\vec{\textbf{a}}}_i}, \dots, {\vec{\textbf{a}}}_3}^{\delta_1, \dots, \widehat{\delta_i}, \dots, \delta_3}(j)} \textrm{dev}\left( (m{\mathcal C})_{{\vec{\textbf{a}}}_i}^{\delta_i} (j), y' \right)}{2^j}\right] \end{align*} $$

is the limit

$$ \begin{align*}\lim_{j \to \infty} \frac{2^{j+1}/3 - 1/5}{2^j} = \frac{2}{3}. \end{align*} $$

This verifies Condition (ii) in Theorem 8.1.▪