Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-13T19:52:49.831Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Geometry of 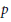$p$-Typical Covers in Characteristic 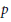$p$

Published online by Cambridge University Press:  20 November 2018

Kiran S. Kedlaya
Kiran S. Kedlaya*
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, U.S.A. e-mail: kedlaya@math.mit.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For 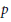$p$ a prime, a 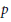$p$-typical cover of a connected scheme on which 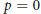$p\,=\,0$ is a finite étale cover whose monodromy group (i.e.,the Galois group of its normal closure) is a 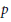$p$-group. The geometry of such covers exhibits some unexpectedly pleasant behaviors; building on work of Katz, we demonstrate some of these. These include a criterion for when a morphism induces an isomorphism of the 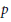$p$-typical quotients of the étale fundamental groups, and a decomposition theorem for 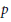$p$-typical covers of polynomial rings over an algebraically closed field.

Keywords

14F35
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 1 , 01 February 2008 , pp. 140 - 163
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Abbes, A. and Saito, T., Ramification of local fields with imperfect residue fields. Amer. J. Math. 124(2002), no. 5, 879–920.Google Scholar
[2] Borger, J. M., Conductors and the moduli of residual perfection. Math. Ann. 329(2004), no. 1, 1–30.Google Scholar
[3] Grothendieck, A. et al., Revêtements étales et groupe fondamental (SGA 1). Lecture Notes in Mathematics 224, Springer-Verlag, Berlin, 1971.Google Scholar
[4] Grothendieck, A. et al., Théorie des topos et cohomologie étale des schémas. I. II. III. (SGA 4). Lecture Notes in Mathematics 269, 270, 305, Springer-Verlag,Google Scholar
[5] Katz, N. M., Local-to-global extensions of representations of fundamental groups. Ann. Inst. Fourier (Grenoble) 36(1986), no. 4, 69–106.Google Scholar
[6] Laumon, G., Semi-continuité du conducteur de Swan (d’après P. Deligne). In: The Euler-Poincaré characteristic (French). Astérisque 83, Soc. Math. France, Paris, 1981, pp. 173–219.Google Scholar
[7] Milne, J. S., Étale cohomology. Princeton Mathematical Series 33, Princeton University Press, Princeton, NJ, 1980.Google Scholar
[8] Serre, J.-P., Local Fields. Graduate Texts in Mathematics 67, Springer-Verlag, New York, 1979.Google Scholar