Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T05:57:32.339Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Normal Growth of Prime Factors of Integers

Published online by Cambridge University Press:  20 November 2018

J. M. De Koninck ,
I. Kátai  and
A. Mercier
J. M. De Koninck
Affiliation:
Département de mathématiques et de statistique, Université Laval, Québec, G1K7P4
I. Kátai
Affiliation:
Eötvös Loránd University, Computer Center, 1117 Budapest, Bogdánfy u. 10/B, Hungary
A. Mercier
Affiliation:
Département de mathématiques, Université du Québec, Chicoutimi, Québec, G7H 2B1
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let h: [0,1] → R be such that 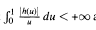and define 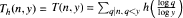.In 1966, Erdős [8] proved that 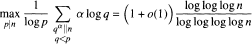holds for almost all n, which by using a simple argument implies that in the case h(u) = u, for almost all n, 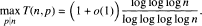He further obtained that, for every z > 0 and almost all n, 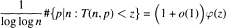and that 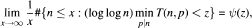where ϕ, ψ, are continuous distribution functions. Several other results concerning the normal growth of prime factors of integers were obtained by Galambos [10], [11] and by De Koninck and Galambos [6].

Let χ = ﹛xm : w ∈ N﹜ be a sequence of real numbers such that limm→∞ xm = +∞. For each x ∈ χ let 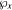be a set of primes p ≤x. Denote by p(n) the smallest prime factor of n. In this paper, we investigate the number of prime divisors p of n, belonging to 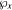for which Th(n,p) > z. Given Δ < 1, we study the behaviour of the function 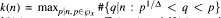We also investigate the two functions 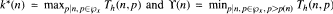, where, in each case, h belongs to a large class of functions.

Keywords

11K6511N2511N35prime factorsdistribution functionscontinuity module
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 44 , Issue 6 , 01 December 1992 , pp. 1121 - 1154
Copyright
Copyright © Canadian Mathematical Society 1992

References

1. Bovey, J.D., On the size of prime factors of integers, Acta. Arith. 33(1977), 65–80.Google Scholar
2. de Bruijn, N.G., On the number of uncancelled elements in the sieve of Eratosthenes, Nederl. Akad. Wetensch., Proc. 53, 803-812. Indagationes Math. 12(1950), 247–256.Google Scholar
3. de Bruijn, N.G., On the number of positive integers ≤ x and free of prime factor s > y, Koninkl. Nederl. Akademie Van Wetenschappen, Series A 54(1951), 49–60.+y,+Koninkl.+Nederl.+Akademie+Van+Wetenschappen,+Series+A+54(1951),+49–60.>Google Scholar
4. De Koninck, J.M., Kátai, I. and Mercier, A., Additive functions monotonie on the set of primes, Acta Arith. 57(1991), 41–68.Google Scholar
5. De Koninck, J.M., Continuity module of the distribution of additive functions related to the largest prime factors of integers, Arch. Math. 55(1990), 450–461.Google Scholar
6. De Koninck, J.M. and Galambos, J., The intermediate prime divisors of integers, Proc. Amer. Math. Soc. 101(1987), 213–216.Google Scholar
7. Erdős, P., Some remarks about additive and multiplicative functions, Bull. Amer. Math. Soc. 52(1946), 527–537.Google Scholar
8. Erdős, P., On some properties of prime factors of integers, Nagoya Math. J. 27(1966), 617–623.Google Scholar
9. Fainleib, A.S., A generalization ofEsseen 's inequality and its application in probabilistic number theory, Izvest. Akad. Nauk SSSR, Ser. Mat. 32 (1968), 859–879. English Transi, in Math. USSR Izvest. 2(1968).Google Scholar
10. Galambos, J., The sequences of prime divisors of integers, Acta Arith. 31(1976), 213–218.Google Scholar
11. Galambos, J., On a problem of Erd P.ôs on large prime divisors ofn and n +1, J. London Math. Soc. 13(1976), 360–362.Google Scholar
12. Galambos, J., Advanced Probability Theory, Marcel Dekker, New York, Basel, 1988.Google Scholar
13. Halberstam, H. and Roth, K.F., Sequences, Clarendon Press, Oxford, 1966.Google Scholar
14. Hardy, G.H. and Ramanujan, , The total number of prime factors of a number n, Quart. J. Math. (Oxford) 48(1917), 76–92.Google Scholar
15. Hensley, D., The convolution powers of the Dickman function, J. London Math. Soc. (2) 33(1986), 395–406.Google Scholar
16. Kubilius, J., Probabilistic Methods in the Theory of Numbers, Translations of Mathematical Monographs, Vol. 11, AMS, Providence, R.I., 1964.Google Scholar
17. Postnikov, A.G., Introduction to Analytic Number Theory, AMS, 1968.Google Scholar
18. Seneta, E., Regularly varying functions, (LNM 508), Springer-Verlag, Berlin, Heidelberg, New York, 1976.Google Scholar
19. Zolotarev, V.M., One-dimensional stable distributions, Translations of Mathematical Monographs, AMS, Volume 65, Providence, Rhode Island, 1986.Google Scholar