No CrossRef data available.
Article contents
On the Number of Associative Triples in an Algebra of n Elements
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Consider a set of n elements α1, … , αn (denoted by S) and the set of all possible multiplication tables on these elements. The total number of such tables is clearly 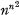 and each table can be represented by a square matrix [μij ] where μij is the product αiαj (μij ∈ S, i = 1, … , n; j = 1, … , n). The triple (αi, αj, αk) is said to be associative if the following equation is satisfied:
and each table can be represented by a square matrix [μij ] where μij is the product αiαj (μij ∈ S, i = 1, … , n; j = 1, … , n). The triple (αi, αj, αk) is said to be associative if the following equation is satisfied:
1.1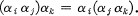
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1967
References
1.
Climescu, A. C.,
Etudes sur la théorie des systèmes multiplicatifs uniformes. I—L'indice de non-associativité, Bull. Ecole Polytech. Jassy,
2 (1947), 347–371.Google Scholar
2.
Straus, E. G. and Wilf, H. S., Combinatorial aspects of the associative law of arithmetic (unpublished).Google Scholar

