Article contents
On the Number of Automorphisms of a Finite p-group
Published online by Cambridge University Press: 20 November 2018
Extract
In this paper we find a new bound for the function g(h), for which |A(G)|p ≧ pn whenever |G| ≧ pg(h) G a finite p-group. The existence of such a function was first conjectured by W. R. Scott in 1954, who proved that g (2) = 3. In 1956 Ledermann and Neumann proved that in the general case of finite groups g(h) ≦ (h – 1)3.-pn−1 + h[10]. Since then, J. A. Green, J. C. Howarth and K. H. Hyde have reduced this bound considerably. The best (least) bound to date for finite p-groups was obtained by K. H. Hyde [9]. He proved that 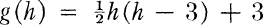 for h ≧ 5 and g(h) = h + 1 for h ≦ 4. For finite non-abelian p-groups, we improve this bound to:
for h ≧ 5 and g(h) = h + 1 for h ≦ 4. For finite non-abelian p-groups, we improve this bound to: 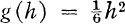 for h ≧ 13, g(h) = 2h – 5 for 5 < h ≦ 8, g(h) = h for h ≦ 5 and for 8 < h ≦ 12 we prove that g(9) = 14, g(10) = 17, g(11) = 20, g(12) = 23.
for h ≧ 13, g(h) = 2h – 5 for 5 < h ≦ 8, g(h) = h for h ≦ 5 and for 8 < h ≦ 12 we prove that g(9) = 14, g(10) = 17, g(11) = 20, g(12) = 23.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1980
References
- 2
- Cited by


