Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-15T07:48:11.869Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Number of Vertices of a Convex Polytope

Published online by Cambridge University Press:  20 November 2018

Victor Klee
Victor Klee*
Affiliation:
University of Washington and Boeing Scientific Research Laboratories
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

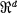As is well known, the theory of linear inequalities is closely related to the study of convex polytopes. If the bounded subset P of euclidean d-space has a non-empty interior and is determined by i linear inequalities in d variables, then P is a d-dimensional convex polytope (here called a d-polytope) which may have as many as i faces of dimension d — 1, and the vertices of this polytope are exactly the basic solutions of the system of inequalities. Thus, to obtain an upper estimate of the size of the computation problem which must be faced in solving a system of linear inequalities, it suffices to find an upper bound for the number f0(P) of vertices of a d-polytope P which has a given number fd-1(P) of (d — l)-faces. A weak bound of this sort was found by Saaty (14), and several authors have posed the problem of finding a sharp estimate.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 16 , 1964 , pp. 701 - 720
Copyright
Copyright © Canadian Mathematical Society 1964

References

1. Br, M.ückner, Ùber die Ableitung der allgemeinen Poly tope und die nach Isomorphismus verschiedenen Typen der allgemeinen Achtzelle (Oktatope), Verh. Nederl. Akad. Wetensch. Sect. I, 10 (1909), 1–27.Google Scholar
2. Carath, C.éodory, Über den Variabilitätsbereich der Fourier schen Konstanten von positiven harmonischen Funktionen, Rend. Circ. Mat. Palermo, 32 (1911), 193–217.Google Scholar
3. Dantzig, George B., Ten unsolved problems (Hectographed notes; Berkeley, 1962).Google Scholar
4. Davis, Chandler, Remarks on a previous paper, Michigan Math. J., 2 (1953), 23–25.Google Scholar
5. Euler, L., Elementa doctrinae solidorum—Demonstratio nonnullarum insignium porprietatum, quibus solida hedris planis inclusa sunt praedita, Novi Comment. Acad. Sci. Imp. Petropol., 4 (1752-53), 1–60.Google Scholar
6. Fieldhouse, Martin, Linear programming, Ph.D. thesis, Cambridge Univ., 1961 (Reviewed in Operations Res., 10 (1962), 740.Google Scholar
7. Gale, David, Neighboring vertices on a convex polytope. Linear Inequalities and Related Systems (Princeton, 1958), pp. 255–263.Google Scholar
8. Gale, David, Neighborly and cyclic polytopes, Proceedings of Symposia in Pure Mathematics, vol. 7, Convexity (Amer. Math. Soc, 1963), pp. 225–232.Google Scholar
9. Gale, David, On the number of faces of a convex polytope. Can. J. Math., 16 (1964), 12–17.Google Scholar
10. Jacobs, W. W. and Schell, E. D., The number of vertices of a convex polytope, Amer. Math. Monthly, 66 (1959), 643.Google Scholar
11. Klee, Victor, Some characterizations of convex polyhedra, Acta Math., 102 (1959), 79–107.Google Scholar
12. Klee, Victor, A combinatorial analogue of Poincaré's duality theorem, Can. J. Math., 16 (1964), 517–531.Google Scholar
13. Motzkin, T. S., Comonotone curves and polyhedra, Abstract III, Bull. Amer. Math. Soc, 63 (1957), 35.Google Scholar
14. Saaty, T. L., The number of vertices of a polyhedron, Amer. Math. Monthly, 62 (1955), 326–331.Google Scholar
15. Weyl, H., Elementare Théorie der konvexen Polyeder, Comment. Math. Helv., 7 (1935), 290–306.—English translation by H. W. Kuhn in Contributions to the theory of games (Princeton, 1950), pp. 3-18.Google Scholar
16. Eggleston, H. G., Grunbaum, Branko, and Klee, Victor, Some semicontinuity theorems for convex polytopes and cell-complexes, Comment. Math. Helv., 89 (1964-65), to appear.Google Scholar