Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-15T06:29:11.890Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Partially Ordered Set of Prime Ideals of a Distributive Lattice

Published online by Cambridge University Press:  20 November 2018

Raymond Balbes
Raymond Balbes*
Affiliation:
University of Missouri, St. Louis, Missouri
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a distributive lattice L, let denote the poset of all prime ideals of L together with ∅ and L. This paper is concerned with the following type of problem. Given a class 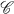of distributive lattices, characterize all posets P for which for some . Such a poset P will be called representable over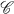. For example, if 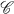is the class of all relatively complemented distributive lattices, then P is representable over 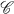if and only if P is a totally unordered poset with 0, 1 adjoined. One of our main results is a complete characterization of those posets P which are representable over the class of distributive lattices which are generated by their meet irreducible elements. The problem of determining which posets P are representable over the class of all distributive lattices appears to be very difficult.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 23 , Issue 5 , October 1971 , pp. 866 - 874
Copyright
Copyright © Canadian Mathematical Society 1971

Footnotes

This research was supported, in part, by NSF Grant GP11893.

References

1. Balbes, R., Projective and injective distributive lattices, Pacific J. Math. 21 (1967), 405–420.Google Scholar
2. Grätzer, G., Lattice theory: First concepts and distributive lattices (Freeman, San Francisco, 1971).Google Scholar
3. Nachbin, L., Une propriété characteristique des algébres Booléiennes, Portugal. Math. 6 (1947), 115–118.Google Scholar
4. Stone, M. H., Topological representations of distributive lattices and Browerian logics, Casopis Pěst. Mat. 67 (1937), 1–25.Google Scholar