Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
BİSWAS, Tanmay
and
BISWAS, Chınmay
2022.
Generalized relative Nevanlinna order (α,β) and generalized relative Nevanlinna type (α,β) based some growth properties of composite analytic functions in the unit disc.
Communications Faculty Of Science University of Ankara Series A1Mathematics and Statistics,
Vol. 71,
Issue. 1,
p.
226.

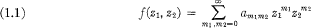
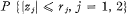 . Let
. Let