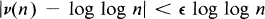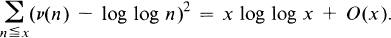Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kátai, I.
1991.
On the number of prime factors of ϕ(ϕ(n)).
Acta Mathematica Hungarica,
Vol. 58,
Issue. 1-2,
p.
211.
Murty, M. Ram
1994.
Finitely generated groups (mod 𝑝).
Proceedings of the American Mathematical Society,
Vol. 122,
Issue. 1,
p.
37.
Marie-Jeanne, F.
and
Tenenbaum, G.
1998.
Une propriété de concentration relative à la fonction d'Euler.
Indagationes Mathematicae,
Vol. 9,
Issue. 3,
p.
383.
Murty, M. Ram
2002.
Current Trends in Number Theory.
p.
111.
Ramaré, Olivier
2022.
Excursions in Multiplicative Number Theory.
p.
251.


 , the number of natural numbers not exceeding
, the number of natural numbers not exceeding