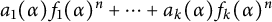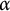Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Scoones, Andrew
2024.
On the abc$abc$ conjecture in algebraic number fields.
Mathematika,
Vol. 70,
Issue. 1,