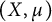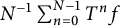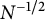1 Introduction and main results
Let
![]() $(X, \mu )$
be a probability space, and let T be a bounded linear operator on the Hilbert space
$(X, \mu )$
be a probability space, and let T be a bounded linear operator on the Hilbert space
![]() $L^2(X,\mu )$
. For
$L^2(X,\mu )$
. For
![]() $f\in L^2(X,\mu ),$
consider its ergodic means
$f\in L^2(X,\mu ),$
consider its ergodic means
 $$\begin{align*}\frac{1}{N}\sum_{n=1}^{N-1}T^nf(x), \quad N \geq 1, x \in X. \end{align*}$$
$$\begin{align*}\frac{1}{N}\sum_{n=1}^{N-1}T^nf(x), \quad N \geq 1, x \in X. \end{align*}$$
In this article, we study the speed of convergence of such ergodic means when T is a unilateral or bilateral shift operator. Shift operators are sometimes induced by ergodic transformations. Thus, our results also cover some particular instances of von Neumann’s [Reference von NeumannvN32] and Birkhoff’s [Reference BirkhoffBir31] ergodic theorems. It is well-known that, in full generality, Birkhoff’s and von Neumann’s theorems are optimal, in the sense that the speed of convergence can indeed be arbitrarily slow, either in norm or in the sense of almost everywhere convergence (see [Reference Kakutani and PetersenKP81, Reference KrengelKre79], cf. Theorem 1.2). Nonetheless, scholars have been intensively investigating such problems from different perspectives and with different goals in mind. To keep track of the literature, as it often happens, is a hard task and here we recall only a few meaningful papers, apologizing for the ones we omit. In [Reference Furman and ShalomFS99], Furman and Shalom consider the measure-preserving and ergodic action of a locally compact group acting on a probability space and study the ergodic properties of the action along random walks on G. The setting described in [Reference Furman and ShalomFS99] is quite different from ours, however, the results obtained are similar in the spirit with the ones we obtain here (cf. [Reference Furman and ShalomFS99, Theorem 1.2] with Theorem 1.4). Kachurovskiı̆, Podvigin, and coauthors have been studying the problem for the last decades from the spectral theory point of view and we refer the reader to the survey [Reference Kachurovskiĭ and PodviginKP16]. In the same spirit of the work of Kachurovskiı̆ and collaborators, we also mention the work [Reference Ben-Artzi and MorisseBAM21]. Avigad and collaborators investigated the rate of convergence in [Reference Avigad, Gerhardy and TowsnerAGT10, Reference Avigad and IovinoAI13, Reference Avigad and RuteAR15] in the sense of metastability (see [Reference TaoTao12]). Finally, we mention the work of Das and Yorke [Reference Das and YorkeDY18], of Bayart, Buczolich, and Heureaux [Reference Bayart, Buczolich and HeurteauxBBH20] and of Colzani, Gariboldi, and Monguzzi [Reference ColzaniCol22, Reference Colzani, Gariboldi and MonguzziCGM24], who all obtain the results on the speed of convergence when one considers as transformation the map
![]() $x\to x+\alpha $
, which is an ergodic transformation of the d-dimensional torus
$x\to x+\alpha $
, which is an ergodic transformation of the d-dimensional torus
![]() $\mathbb T^d={\mathbb {R}}^d/{\mathbb {Z}}^d$
whenever
$\mathbb T^d={\mathbb {R}}^d/{\mathbb {Z}}^d$
whenever
![]() $\alpha =(\alpha _1,\ldots ,\alpha _d)$
is an irrational vector, that is, whenever
$\alpha =(\alpha _1,\ldots ,\alpha _d)$
is an irrational vector, that is, whenever
![]() $1,\alpha _1,\ldots ,\alpha _d$
are linearly independent over
$1,\alpha _1,\ldots ,\alpha _d$
are linearly independent over
![]() $\mathbb Q$
.
$\mathbb Q$
.
In order to provide some context for our results, let us focus for a moment on a specific transformation, namely, the doubling map
![]() $x\mapsto 2x\mod 1$
, which is a well-known ergodic transformation of the one-dimensional torus
$x\mapsto 2x\mod 1$
, which is a well-known ergodic transformation of the one-dimensional torus
![]() $\mathbb T$
. The sum
$\mathbb T$
. The sum
![]() $\sum _{n=0}^{N-1} f(2^nx)$
satisfies the central limit theorem and the law of iterated logarithm for a large class of functions. See the work of Fortet [Reference FortetFor40], Kac [Reference KacKac46], and Maruyama [Reference MaruyamaMar50]. For subsequent extension of these results we mention, among others, the works of Aistleitner [Reference AistleitnerAis10, Reference AistleitnerAis13] and refer to the references therein. More in detail, Maruyama, building upon the results of Kac, proved that if f is a continuous function with vanishing mean and satisfying a Hölder condition of order
$\sum _{n=0}^{N-1} f(2^nx)$
satisfies the central limit theorem and the law of iterated logarithm for a large class of functions. See the work of Fortet [Reference FortetFor40], Kac [Reference KacKac46], and Maruyama [Reference MaruyamaMar50]. For subsequent extension of these results we mention, among others, the works of Aistleitner [Reference AistleitnerAis10, Reference AistleitnerAis13] and refer to the references therein. More in detail, Maruyama, building upon the results of Kac, proved that if f is a continuous function with vanishing mean and satisfying a Hölder condition of order
![]() $\alpha>0$
, then, for almost every x,
$\alpha>0$
, then, for almost every x,
 $$\begin{align*}\limsup_{N\to+\infty}\frac{1}{\sqrt{2N\log\log(N)}}\sum_{n=0}^{N-1} f(2^nx)= \lim_{N\to+\infty}\bigg( \frac{1}{N}\int_{\mathbb T} \Big(\sum_{n=0}^{N-1} f(2^ny)\Big)^2\, dy\bigg)^{\frac{1}{2}}. \end{align*}$$
$$\begin{align*}\limsup_{N\to+\infty}\frac{1}{\sqrt{2N\log\log(N)}}\sum_{n=0}^{N-1} f(2^nx)= \lim_{N\to+\infty}\bigg( \frac{1}{N}\int_{\mathbb T} \Big(\sum_{n=0}^{N-1} f(2^ny)\Big)^2\, dy\bigg)^{\frac{1}{2}}. \end{align*}$$
The point of view in the papers, we mentioned focuses on the lacunarity of the sequence
![]() $\{2^nx\}_{n\in \mathbb N}$
and on the analogy with systems of independent random variables. In this work, instead, we take advantage of the fact that the composition operator
$\{2^nx\}_{n\in \mathbb N}$
and on the analogy with systems of independent random variables. In this work, instead, we take advantage of the fact that the composition operator
![]() $Tf(x)=f(2x)$
is a shift operator on
$Tf(x)=f(2x)$
is a shift operator on
![]() $L^2(\mathbb T, dx)$
(see below for the exact definition).
$L^2(\mathbb T, dx)$
(see below for the exact definition).
Before stating our results, we briefly recall some definitions following [Reference Sz.-Nagy, Foias, Bercovici and KérchySNFBK10]. Let
![]() $\mathcal H$
be a complex separable Hilbert space endowed with the inner product
$\mathcal H$
be a complex separable Hilbert space endowed with the inner product
![]() $\langle \cdot ,\cdot \rangle $
. Let
$\langle \cdot ,\cdot \rangle $
. Let
![]() $T:\mathcal H\to \mathcal H$
be an isometry, that is, a bounded linear operator such that
$T:\mathcal H\to \mathcal H$
be an isometry, that is, a bounded linear operator such that
A subspace
![]() $\mathcal V\subseteq \mathcal H$
is called a wandering subspace for the isometry
$\mathcal V\subseteq \mathcal H$
is called a wandering subspace for the isometry
![]() $T:\mathcal H\to \mathcal H$
if
$T:\mathcal H\to \mathcal H$
if
The isometry
![]() $T:\mathcal H\to \mathcal H$
is a unilateral shift if there exists a wandering subspace
$T:\mathcal H\to \mathcal H$
is a unilateral shift if there exists a wandering subspace
![]() $\mathcal V\subseteq \mathcal H$
for T such that
$\mathcal V\subseteq \mathcal H$
for T such that
In this case, we say that the subspace
![]() $\mathcal V$
is a generating wandering subspace for T. Notice that
$\mathcal V$
is a generating wandering subspace for T. Notice that
Unilateral shifts are ubiquitous in operator theory. One reason for this is provided by Wold’s decomposition theorem (see, e.g., [Reference Sz.-Nagy, Foias, Bercovici and KérchySNFBK10, Chapter 1]).
Theorem 1.1 (Wold decomposition)
Let
![]() $T:\mathcal H\to \mathcal H$
be an isometry. Then,
$T:\mathcal H\to \mathcal H$
be an isometry. Then,
where
![]() $\mathcal M$
and
$\mathcal M$
and
![]() $\mathcal M^\perp $
are invariant under T,
$\mathcal M^\perp $
are invariant under T,
![]() $T:\mathcal M\to \mathcal M$
is a unilateral shift and
$T:\mathcal M\to \mathcal M$
is a unilateral shift and
![]() ${T:\mathcal M^\perp \to \mathcal M^\perp} $
is a unitary operator. Such decomposition is uniquely determined and it holds
${T:\mathcal M^\perp \to \mathcal M^\perp} $
is a unitary operator. Such decomposition is uniquely determined and it holds
Similarly to unilateral shifts, it is possible to define bilateral shifts. A subspace
![]() ${\mathcal V\subseteq \mathcal H}$
is called a wandering subspace for the unitary operator
${\mathcal V\subseteq \mathcal H}$
is called a wandering subspace for the unitary operator
![]() $T:\mathcal H\to \mathcal H$
if
$T:\mathcal H\to \mathcal H$
if
and
![]() $T:\mathcal H\to \mathcal H$
is a bilateral shift if there exists a generating wandering subspace
$T:\mathcal H\to \mathcal H$
is a bilateral shift if there exists a generating wandering subspace
![]() ${\mathcal V\subseteq \mathcal H}$
such that
${\mathcal V\subseteq \mathcal H}$
such that
Notice that for bilateral shifts the generating wandering subspace is not uniquely determined.
If
![]() $T:\mathcal H\to \mathcal H$
is a shift, then
$T:\mathcal H\to \mathcal H$
is a shift, then
![]() $\mathcal H$
admits an orthonormal basis of the form
$\mathcal H$
admits an orthonormal basis of the form
![]() $\{\varphi _{j,k}\}_{j\in \mathbb X, k\in \mathbb Y}$
, where
$\{\varphi _{j,k}\}_{j\in \mathbb X, k\in \mathbb Y}$
, where
![]() $\mathbb X\subseteq \mathbb N$
and
$\mathbb X\subseteq \mathbb N$
and
![]() $\mathbb Y$
is either
$\mathbb Y$
is either
![]() $\mathbb N\cup \{0\}$
or
$\mathbb N\cup \{0\}$
or
![]() $\mathbb Z$
depending on T being a unilateral or bilateral shift, such that
$\mathbb Z$
depending on T being a unilateral or bilateral shift, such that
![]() $\{\varphi _{j,k}\}_{j\in \mathbb X}$
is an orthonormal basis for
$\{\varphi _{j,k}\}_{j\in \mathbb X}$
is an orthonormal basis for
![]() $T^k(\mathcal V)$
for every
$T^k(\mathcal V)$
for every
![]() $k\in \mathbb Y$
and such that, for every fixed
$k\in \mathbb Y$
and such that, for every fixed
![]() $k\in \mathbb Y$
, it holds
$k\in \mathbb Y$
, it holds
From now on when, we say that the isometry
![]() $T:\mathcal H\to \mathcal H$
is a shift we mean that T could be either a unilateral or a bilateral shift. However, the reader has to keep in mind that whenever T is intended as a bilateral shift then T is not only an isometry, but a unitary operator as well.
$T:\mathcal H\to \mathcal H$
is a shift we mean that T could be either a unilateral or a bilateral shift. However, the reader has to keep in mind that whenever T is intended as a bilateral shift then T is not only an isometry, but a unitary operator as well.
We now introduce the general setting in which our results take place. We will assume the following:
-
(i)
 $\mathcal H$
is a Hilbert space and
$\mathcal H$
is a Hilbert space and
 $T:\mathcal H\to \mathcal H$
is an isometry.
$T:\mathcal H\to \mathcal H$
is an isometry. -
(ii)
 $\mathcal H= \mathcal M\oplus \mathcal M^\perp $
, where
$\mathcal H= \mathcal M\oplus \mathcal M^\perp $
, where
 $T\vert _{\mathcal M}: \mathcal M\to \mathcal M$
is a shift (bilateral or unilateral) and
$T\vert _{\mathcal M}: \mathcal M\to \mathcal M$
is a shift (bilateral or unilateral) and
 $T\vert _{\mathcal M^{\perp }}: \mathcal M^\perp \to \mathcal M^\perp $
is the identity operator; i.e., we are considering isometries whose unitary part in the Wold decomposition is the identity operator.
$T\vert _{\mathcal M^{\perp }}: \mathcal M^\perp \to \mathcal M^\perp $
is the identity operator; i.e., we are considering isometries whose unitary part in the Wold decomposition is the identity operator. -
(iii)
 $\mathcal V$
is a generating wandering subspace for
$\mathcal V$
is a generating wandering subspace for
 $T\vert _{\mathcal M}$
and
$T\vert _{\mathcal M}$
and
 $\Pi _{\mathcal M^\perp }$
and
$\Pi _{\mathcal M^\perp }$
and
 $\Pi _k$
are the orthogonal projections from
$\Pi _k$
are the orthogonal projections from
 $\mathcal H$
onto
$\mathcal H$
onto
 $\mathcal M^\perp $
and
$\mathcal M^\perp $
and
 $T^{k}(\mathcal V),$
respectively. Here, k varies either in
$T^{k}(\mathcal V),$
respectively. Here, k varies either in
 $\mathbb N\cup \{0\}$
or
$\mathbb N\cup \{0\}$
or
 $\mathbb Z$
accordingly with the fact that T is a unilateral or a bilateral shift.
$\mathbb Z$
accordingly with the fact that T is a unilateral or a bilateral shift.
The following theorem is implicit in the existing literature, but we could not find a precise reference. In particular, when T is a shift such that
![]() $\dim (\mathcal {V}) = + \infty ,$
the theorem is proved in [Reference KrengelKre79] and [Reference Kakutani and PetersenKP81]. Anyhow, a short proof will be included for the reader’s convenience.
$\dim (\mathcal {V}) = + \infty ,$
the theorem is proved in [Reference KrengelKre79] and [Reference Kakutani and PetersenKP81]. Anyhow, a short proof will be included for the reader’s convenience.
Theorem 1.2 With the notation above, for every positive vanishing sequence
![]() $\varepsilon _n\to 0$
as
$\varepsilon _n\to 0$
as
![]() $n\to +\infty $
, there exists
$n\to +\infty $
, there exists
![]() $f\in \mathcal H$
such that
$f\in \mathcal H$
such that
 $$\begin{align*}\limsup_{N\to +\infty} \varepsilon_N^{-1} \bigg\Vert\frac{1}{N}\sum_{n=0}^{N-1} T^nf-\Pi_{\mathcal M^\perp}f\bigg\Vert_{\mathcal H}=+\infty. \end{align*}$$
$$\begin{align*}\limsup_{N\to +\infty} \varepsilon_N^{-1} \bigg\Vert\frac{1}{N}\sum_{n=0}^{N-1} T^nf-\Pi_{\mathcal M^\perp}f\bigg\Vert_{\mathcal H}=+\infty. \end{align*}$$
Despite the negative result in the previous theorem, it is possible to give some positive results on the speed convergence under appropriate assumptions on the operator and on the functions. The following result is no surprising and we include it for the sake of completeness.
Theorem 1.3 With the notation above,
 $$ \begin{align*} \bigg\Vert\frac{1}{N}&\sum_{n=0}^{N-1} T^nf-\Pi_{\mathcal M^\perp}f\bigg\Vert_{\mathcal H}\leq \frac{1}{\sqrt{N}}\sum_{k} \Vert\Pi_k f\Vert_{\mathcal H}. \end{align*} $$
$$ \begin{align*} \bigg\Vert\frac{1}{N}&\sum_{n=0}^{N-1} T^nf-\Pi_{\mathcal M^\perp}f\bigg\Vert_{\mathcal H}\leq \frac{1}{\sqrt{N}}\sum_{k} \Vert\Pi_k f\Vert_{\mathcal H}. \end{align*} $$
Moreover, the rate of convergence
![]() $1/\sqrt {N}$
is sharp.
$1/\sqrt {N}$
is sharp.
The next theorem is our first main one. We obtain a result on the pointwise speed of convergence and the boundedness of a maximal function.
Theorem 1.4 With the notation above, assume that
![]() $\mathcal H$
is the function space
$\mathcal H$
is the function space
![]() ${L^2_\mu := L^2(X,d\mu ),}$
where
${L^2_\mu := L^2(X,d\mu ),}$
where
![]() $(X, \mu )$
is a probability space, and that
$(X, \mu )$
is a probability space, and that
![]() $\varepsilon :\mathbb R_+\to \mathbb R_+$
is a positive decreasing function. Define the maximal operator
$\varepsilon :\mathbb R_+\to \mathbb R_+$
is a positive decreasing function. Define the maximal operator
 $$\begin{align*}Sf (x) = \sup_{N\geq 1} N\varepsilon(N)\bigg\vert \dfrac{1}{N} \sum_{n=0}^{N-1} T^n f (x) - \Pi_{\mathcal M^\perp}f(x) \bigg\vert. \end{align*}$$
$$\begin{align*}Sf (x) = \sup_{N\geq 1} N\varepsilon(N)\bigg\vert \dfrac{1}{N} \sum_{n=0}^{N-1} T^n f (x) - \Pi_{\mathcal M^\perp}f(x) \bigg\vert. \end{align*}$$
Then, there exists a positive constant c such that
 $$ \begin{align} \Vert S f\Vert_{L^2(X,\mu)}\leq c \bigg( \sum_{n=0}^{+\infty} \varepsilon^2(n) \log^2(n+2) \bigg)^{\frac{1}{2}}\sum_{k} \Vert\Pi_k f\Vert_{L^2_{\mu}}. \end{align} $$
$$ \begin{align} \Vert S f\Vert_{L^2(X,\mu)}\leq c \bigg( \sum_{n=0}^{+\infty} \varepsilon^2(n) \log^2(n+2) \bigg)^{\frac{1}{2}}\sum_{k} \Vert\Pi_k f\Vert_{L^2_{\mu}}. \end{align} $$
Moreover, if
 $$ \begin{align} \sum_{n=0}^{+\infty} \varepsilon^2(n) \log^2(n+2) < +\infty \quad \text{and} \quad \sum_{k} \Vert\Pi_k f\Vert_{L^2_{\mu}} <+\infty, \end{align} $$
$$ \begin{align} \sum_{n=0}^{+\infty} \varepsilon^2(n) \log^2(n+2) < +\infty \quad \text{and} \quad \sum_{k} \Vert\Pi_k f\Vert_{L^2_{\mu}} <+\infty, \end{align} $$
then, for
![]() $\mu $
-almost every x,
$\mu $
-almost every x,
 $$ \begin{align} \lim_{N\to+\infty} N\varepsilon(N)\bigg\vert\frac{1}{N} \sum_{n=0}^{N-1} T^n f (x) - \Pi_{\mathcal M^\perp}f(x) \bigg\vert= 0. \end{align} $$
$$ \begin{align} \lim_{N\to+\infty} N\varepsilon(N)\bigg\vert\frac{1}{N} \sum_{n=0}^{N-1} T^n f (x) - \Pi_{\mathcal M^\perp}f(x) \bigg\vert= 0. \end{align} $$
For example, one can choose
![]() $\varepsilon (n) = n^{-\frac {1}{2}} \log ^{-\delta }(n+2) $
with
$\varepsilon (n) = n^{-\frac {1}{2}} \log ^{-\delta }(n+2) $
with
![]() $\delta>\frac {3}{2}.$
Then equation (1.3) gives a speed of convergence of the ergodic means of T at least of the order of
$\delta>\frac {3}{2}.$
Then equation (1.3) gives a speed of convergence of the ergodic means of T at least of the order of
![]() $ N^{-\frac {1}{2}} \log ^\delta (N+2).$
Some particular instances of the above theorem, in the special case that T is the operator of composition with a measure preserving transformation of X, have been obtained by Cuny [Reference CunyCun11, Theorem 4.5] (see also Remark
$ N^{-\frac {1}{2}} \log ^\delta (N+2).$
Some particular instances of the above theorem, in the special case that T is the operator of composition with a measure preserving transformation of X, have been obtained by Cuny [Reference CunyCun11, Theorem 4.5] (see also Remark
![]() $1$
after Theorem 4.5). The following are two straightforward applications of the above theorem. In Corollary 1.5, we consider functions defined on the square
$1$
after Theorem 4.5). The following are two straightforward applications of the above theorem. In Corollary 1.5, we consider functions defined on the square
![]() $[0,1)^2$
and their expansions with respect to the product Walsh system. We recall the definition of such system in the proof of the corollary. In Corollary 1.6, we consider the system of Laguerre polynomials, whose definition is, once again, recalled in the proof of the corollary. In both the corollaries, the almost every convergence is intended with respect to the Lebesgue measure.
$[0,1)^2$
and their expansions with respect to the product Walsh system. We recall the definition of such system in the proof of the corollary. In Corollary 1.6, we consider the system of Laguerre polynomials, whose definition is, once again, recalled in the proof of the corollary. In both the corollaries, the almost every convergence is intended with respect to the Lebesgue measure.
Corollary 1.5 Let
![]() $B:[0,1)^2\to [0,1)^2$
be the baker’s transformation defined by
$B:[0,1)^2\to [0,1)^2$
be the baker’s transformation defined by
 $$\begin{align*}B(x,y)=\begin{cases} (2x, \frac{y}{2}), & {\textrm{if }} 0\leq x<\frac{1}{2},\\ (2x-1, \frac{y}{2}+\frac{1}{2}), & {\textrm{if }} \frac{1}{2}\leq x<1. \end{cases} \end{align*}$$
$$\begin{align*}B(x,y)=\begin{cases} (2x, \frac{y}{2}), & {\textrm{if }} 0\leq x<\frac{1}{2},\\ (2x-1, \frac{y}{2}+\frac{1}{2}), & {\textrm{if }} \frac{1}{2}\leq x<1. \end{cases} \end{align*}$$
Assume that f has an absolutely convergent expansion with respect to the product Walsh system on the square
![]() $[0,1)^2$
. Then, for every
$[0,1)^2$
. Then, for every
![]() $\eta>0$
and for almost every x,
$\eta>0$
and for almost every x,
 $$\begin{align*}\lim_{N\to+\infty} \frac{\sqrt{N}}{(\log(1+N))^{\frac{3}{2}+\eta}}\bigg\vert\frac{1}{N}\sum_{n=0}^{N-1} f(B^n x)-\int_{[0,1)^2} f(y)\, dy\bigg\vert=0. \end{align*}$$
$$\begin{align*}\lim_{N\to+\infty} \frac{\sqrt{N}}{(\log(1+N))^{\frac{3}{2}+\eta}}\bigg\vert\frac{1}{N}\sum_{n=0}^{N-1} f(B^n x)-\int_{[0,1)^2} f(y)\, dy\bigg\vert=0. \end{align*}$$
Corollary 1.6 Let T be the operator
defined on the Hilbert space
![]() $L^2(\mathbb R_+, e^{-x}\, dx),$
and let
$L^2(\mathbb R_+, e^{-x}\, dx),$
and let
![]() $\{L_n\}_{n\in \mathbb N}$
be the system of Laguerre polynomials. Assume that the Laguerre coefficients of f are absolutely summable. Then, for every
$\{L_n\}_{n\in \mathbb N}$
be the system of Laguerre polynomials. Assume that the Laguerre coefficients of f are absolutely summable. Then, for every
![]() $\eta>0$
and for almost every x,
$\eta>0$
and for almost every x,
 $$\begin{align*}\lim_{N\to+\infty}\frac{\sqrt{N}}{(\log(1+N))^{\frac{3}{2}+\eta}}\bigg\vert \frac{1}{N}\sum_{n=0}^{N-1} T^n f(x) \bigg\vert=0. \end{align*}$$
$$\begin{align*}\lim_{N\to+\infty}\frac{\sqrt{N}}{(\log(1+N))^{\frac{3}{2}+\eta}}\bigg\vert \frac{1}{N}\sum_{n=0}^{N-1} T^n f(x) \bigg\vert=0. \end{align*}$$
Our last theorem is about ergodic means associated with the endomorphisms of the two-dimensional torus
![]() $\mathbb {T}^2=\mathbb {R}^2/\mathbb {Z}^2$
and the classical trigonometric expansion. We prove that it is enough to require a mild summability condition with respect to a logarithmic weight on the Fourier coefficients of a function to gain a speed of convergence essentially of order
$\mathbb {T}^2=\mathbb {R}^2/\mathbb {Z}^2$
and the classical trigonometric expansion. We prove that it is enough to require a mild summability condition with respect to a logarithmic weight on the Fourier coefficients of a function to gain a speed of convergence essentially of order
![]() $N^{-\frac {1}{2}}$
for the ergodic means.
$N^{-\frac {1}{2}}$
for the ergodic means.
Theorem 1.7 Let A be a
![]() $2\times 2$
integer matrix such that
$2\times 2$
integer matrix such that
![]() $\det (A)\neq 0$
and no eigenvalue of A is a root of unity. Assume that
$\det (A)\neq 0$
and no eigenvalue of A is a root of unity. Assume that
![]() $f\in L^2(\mathbb T^2, dx)$
has the trigonometric expansion
$f\in L^2(\mathbb T^2, dx)$
has the trigonometric expansion
and that, for some
![]() $\delta>0$
,
$\delta>0$
,
Then, for every
![]() $\eta>0$
and for almost every
$\eta>0$
and for almost every
![]() $x\in \mathbb T^2$
,
$x\in \mathbb T^2$
,
 $$\begin{align*}\lim_{N\to+\infty} \frac{\sqrt{N}}{(\log(1+N))^{\frac{3}{2}+\eta}}\bigg\vert\frac1{N}\sum_{n=0}^{N-1} f(A^nx)-\int_{\mathbb T^2}f(y)\, dy\bigg\vert=0. \end{align*}$$
$$\begin{align*}\lim_{N\to+\infty} \frac{\sqrt{N}}{(\log(1+N))^{\frac{3}{2}+\eta}}\bigg\vert\frac1{N}\sum_{n=0}^{N-1} f(A^nx)-\int_{\mathbb T^2}f(y)\, dy\bigg\vert=0. \end{align*}$$
We point out that, in the above theorem, A has no eigenvalues which are not roots of unity if and only if A is an ergodic matrix [Reference Einsiedler and WardEW11, Corollary 2.2]. Therefore, the above theorem guarantees a speed a convergence for the ergodic means of a large class of functions for a particular instance of Birkhoff’s ergodic theorem. Condition (1.4) is satisfied, for instance, by functions in any fractional Sobolev space. A more general sufficient condition in terms of the
![]() $L^2$
integral modulus of continuity will be given in Proposition 4.1.
$L^2$
integral modulus of continuity will be given in Proposition 4.1.
The situation in dimension
![]() $d>2$
seems to be more complicated. Nonetheless, we prove the following partial result, which is a corollary of Theorem 1.4.
$d>2$
seems to be more complicated. Nonetheless, we prove the following partial result, which is a corollary of Theorem 1.4.
Corollary 1.8 Let A be a
![]() $d\times d$
matrix with integer coefficients and
$d\times d$
matrix with integer coefficients and
![]() $\det (A)\neq 0$
. Suppose there exists a set
$\det (A)\neq 0$
. Suppose there exists a set
![]() $\mathcal {E} \subseteq {\mathbb {Z}}^d\setminus \{ 0\} $
such that the subspace of
$\mathcal {E} \subseteq {\mathbb {Z}}^d\setminus \{ 0\} $
such that the subspace of
![]() $L^2_0(\mathbb T^d,dx)$
$L^2_0(\mathbb T^d,dx)$
is a generating wandering subspace for the operator
![]() $ T_A f = f \circ A $
. Suppose that there exist
$ T_A f = f \circ A $
. Suppose that there exist
![]() $c>0, q>1 $
, such that for all
$c>0, q>1 $
, such that for all
![]() $\xi \in \mathcal {E}$
and
$\xi \in \mathcal {E}$
and
![]() $k \in \mathbb {Y}$
(where
$k \in \mathbb {Y}$
(where
![]() $\mathbb {Y}$
is either
$\mathbb {Y}$
is either
![]() $\mathbb {N} \cup \{ 0 \} $
or
$\mathbb {N} \cup \{ 0 \} $
or
![]() $\mathbb {Z}$
depending on whether
$\mathbb {Z}$
depending on whether
![]() $T_A$
is a unilateral or bilateral shift),
$T_A$
is a unilateral or bilateral shift),
Assume that
![]() $f\in L^2(\mathbb T^2, dx)$
has the trigonometric expansion
$f\in L^2(\mathbb T^2, dx)$
has the trigonometric expansion
and that, for some
![]() $\delta>0$
,
$\delta>0$
,
Then, for every
![]() $\eta>0$
and for almost every
$\eta>0$
and for almost every
![]() $x\in \mathbb T^2$
,
$x\in \mathbb T^2$
,
 $$\begin{align*}\lim_{N\to+\infty} \frac{\sqrt{N}}{(\log(1+N))^{\frac{3}{2}+\eta}}\bigg\vert\frac1{N}\sum_{n=0}^{N-1} f(A^nx)-\int_{\mathbb T^2}f(y)\, dy\bigg\vert=0. \end{align*}$$
$$\begin{align*}\lim_{N\to+\infty} \frac{\sqrt{N}}{(\log(1+N))^{\frac{3}{2}+\eta}}\bigg\vert\frac1{N}\sum_{n=0}^{N-1} f(A^nx)-\int_{\mathbb T^2}f(y)\, dy\bigg\vert=0. \end{align*}$$
Assumption (1.5) is satisfied, for instance, whenever A is an expansive matrix, i.e., whenever there exists
![]() $q>1$
such that
$q>1$
such that
![]() $\vert Ax\vert \geq q \vert x\vert $
for all
$\vert Ax\vert \geq q \vert x\vert $
for all
![]() $x \in {\mathbb {R}}^d$
.
$x \in {\mathbb {R}}^d$
.
We should also mention that in the literature there exist theorems of flavor similar to Theorem 1.7. For example in [Reference LöbbeLö14, Theorem 1.2], the author proves the law of the iterated logarithm for averages of the form
 $$\begin{align*}\frac 1N\sum_{n=0}^{N-1}f(M_n x), \end{align*}$$
$$\begin{align*}\frac 1N\sum_{n=0}^{N-1}f(M_n x), \end{align*}$$
where
![]() $(M_n)_{n\geq 1}$
is a sequence of integer matrices satisfies a strong Hadamard-type condition [Reference LöbbeLö14, Condition (1.4)] and f is a function of finite Hardy–Krause total variation. Although our theorem gives less precise asymptotic information than the law of the iterated logarithm, our assumptions are much less stringent. If A is a matrix as in Theorem 1.7, then the sequence
$(M_n)_{n\geq 1}$
is a sequence of integer matrices satisfies a strong Hadamard-type condition [Reference LöbbeLö14, Condition (1.4)] and f is a function of finite Hardy–Krause total variation. Although our theorem gives less precise asymptotic information than the law of the iterated logarithm, our assumptions are much less stringent. If A is a matrix as in Theorem 1.7, then the sequence
![]() $M_n:=A^n$
does not in general satisfy [Reference LöbbeLö14, Condition (1.4)] and functions satisfying (1.4) can be quite rough. Furthermore, for matrices with eigenvalues of modulus greater than
$M_n:=A^n$
does not in general satisfy [Reference LöbbeLö14, Condition (1.4)] and functions satisfying (1.4) can be quite rough. Furthermore, for matrices with eigenvalues of modulus greater than
![]() $1$
, Fan [Reference FanFan99] has obtained sharp estimates for the decay of correlation which lead to central limit-type theorems for the distribution of values of the ergodic averages.
$1$
, Fan [Reference FanFan99] has obtained sharp estimates for the decay of correlation which lead to central limit-type theorems for the distribution of values of the ergodic averages.
2 Proof of Theorems 1.2, 1.3, and 1.4 and of Corollaries 1.5 and 1.6
The proof of Theorem 1.2 is straightforward.
Proof of Theorem 1.2
Since T has operator norm
![]() $1$
, the averaging operator
$1$
, the averaging operator
![]() ${U_N:=\frac {1}{N}\sum _{n=0}^{N-1} T^n}$
has operator norm at most
${U_N:=\frac {1}{N}\sum _{n=0}^{N-1} T^n}$
has operator norm at most
![]() $1$
. Furthermore, the norm is at least
$1$
. Furthermore, the norm is at least
![]() $1$
, as it can be seen by testing the operator
$1$
, as it can be seen by testing the operator
![]() $U_N$
on the functions
$U_N$
on the functions
![]() $f_H=\sum _{k=0}^{H}\varphi _{j,k}$
and letting
$f_H=\sum _{k=0}^{H}\varphi _{j,k}$
and letting
![]() ${H\to +\infty} $
. Here,
${H\to +\infty} $
. Here,
![]() $\{\varphi _{j,k}\}_{j,k}$
is an orthonormal basis associated with the shift T. Therefore, the family of operators
$\{\varphi _{j,k}\}_{j,k}$
is an orthonormal basis associated with the shift T. Therefore, the family of operators
![]() $\{\varepsilon ^{-1}_N U_N\}_{N}$
is not uniformly bounded in the operator norm. Hence, by the Banach–Steinhaus uniform boundedness principle, there exists
$\{\varepsilon ^{-1}_N U_N\}_{N}$
is not uniformly bounded in the operator norm. Hence, by the Banach–Steinhaus uniform boundedness principle, there exists
![]() $f\in \mathcal M\subseteq \mathcal H$
such that
$f\in \mathcal M\subseteq \mathcal H$
such that
 $$\begin{align*}\limsup_{N\to+\infty} \varepsilon_N^{-1}\bigg\Vert \frac{1}{N}\sum_{n=0}^{N-1} T^nf\bigg\Vert_{\mathcal H}=+\infty.\\[-42pt] \end{align*}$$
$$\begin{align*}\limsup_{N\to+\infty} \varepsilon_N^{-1}\bigg\Vert \frac{1}{N}\sum_{n=0}^{N-1} T^nf\bigg\Vert_{\mathcal H}=+\infty.\\[-42pt] \end{align*}$$
As mentioned, Theorem 1.3 can also be proved using the unitary equivalence with the shift operator on vector valued Hardy spaces in the unit disc. However, for the sake of completeness, we provide here a direct proof.
Proof of Theorem 1.3
The proof for unilateral or bilateral shifts is the same. Let
![]() ${T:\mathcal M\to \mathcal M}$
be a bilateral shift. Then, there exists a generating wandering subspace
${T:\mathcal M\to \mathcal M}$
be a bilateral shift. Then, there exists a generating wandering subspace
![]() $\mathcal V$
such that
$\mathcal V$
such that
 $$\begin{align*}\mathcal H=\mathcal M\oplus \mathcal M^\perp=\bigg(\bigoplus_{k\in\mathbb Z}T^k\big(\mathcal V\big)\bigg)\oplus \mathcal M^\perp. \end{align*}$$
$$\begin{align*}\mathcal H=\mathcal M\oplus \mathcal M^\perp=\bigg(\bigoplus_{k\in\mathbb Z}T^k\big(\mathcal V\big)\bigg)\oplus \mathcal M^\perp. \end{align*}$$
Let
![]() $\{\varphi _{j,k}\}_{j\in \mathbb X,k\in \mathbb Z}$
be an orthonormal basis of
$\{\varphi _{j,k}\}_{j\in \mathbb X,k\in \mathbb Z}$
be an orthonormal basis of
![]() $\mathcal M$
associated with T. Without losing generality, we assume that f has only finitely many nonzero coefficients
$\mathcal M$
associated with T. Without losing generality, we assume that f has only finitely many nonzero coefficients
![]() $\{\widehat f(j,k)\}_{j\in \mathbb X,k\in \mathbb Z}$
with respect to the orthonormal basis
$\{\widehat f(j,k)\}_{j\in \mathbb X,k\in \mathbb Z}$
with respect to the orthonormal basis
![]() $\{\varphi _{j,k}\}_{j\in \mathbb X,k\in \mathbb Z}$
. Since T acts as the identity on
$\{\varphi _{j,k}\}_{j\in \mathbb X,k\in \mathbb Z}$
. Since T acts as the identity on
![]() $\mathcal M^\perp $
, we have
$\mathcal M^\perp $
, we have
 $$ \begin{align*} \frac{1}{N} \sum_{n=0}^{N-1} T^n f-\Pi_{\mathcal M^\perp}f &= \frac{1}{N} \sum_{n=0}^{N-1} \sum_{j,k}\widehat f(j,k)\varphi_{j,k+n}=\frac{1}{\sqrt N}\sum_{j,k}\widehat f(j,k)\Psi_{j,k}(N), \end{align*} $$
$$ \begin{align*} \frac{1}{N} \sum_{n=0}^{N-1} T^n f-\Pi_{\mathcal M^\perp}f &= \frac{1}{N} \sum_{n=0}^{N-1} \sum_{j,k}\widehat f(j,k)\varphi_{j,k+n}=\frac{1}{\sqrt N}\sum_{j,k}\widehat f(j,k)\Psi_{j,k}(N), \end{align*} $$
where we have set
 $$\begin{align*}\Psi_{j,k}(N)=\frac{1}{\sqrt N} \sum_{n=0}^{N-1} \varphi_{j,k+n}. \end{align*}$$
$$\begin{align*}\Psi_{j,k}(N)=\frac{1}{\sqrt N} \sum_{n=0}^{N-1} \varphi_{j,k+n}. \end{align*}$$
It can be readily checked that
![]() $\{\Psi _{j,k}(N)\}_{j\in \mathbb X}$
is an orthonormal system for every fixed
$\{\Psi _{j,k}(N)\}_{j\in \mathbb X}$
is an orthonormal system for every fixed
![]() $k\in \mathbb Z$
. Hence, by Parserval’s identity,
$k\in \mathbb Z$
. Hence, by Parserval’s identity,
 $$ \begin{align*} \bigg\Vert \frac{1}{N}\sum_{n=0}^{N-1} T^nf-\Pi_{\mathcal M^\perp} f\bigg\Vert&=\bigg\Vert\frac{1}{\sqrt N}\sum_{j,k}\widehat f(j,k)\Psi_{j,k}(N)\bigg\Vert\\ &\leq \frac{1}{\sqrt N}\sum_{k\in\mathbb Z} \bigg\Vert\sum_{j\in\mathbb X}\widehat f(j,k) \Psi_{j,k}(N)\bigg\Vert\\ &= \frac{1}{\sqrt{N}} \sum_{k\in\mathbb Z} \bigg(\sum_{j\in\mathbb X}\vert\widehat f(j,k)\vert^2\bigg)^{\frac{1}{2}}= \frac{1}{\sqrt{N}} \sum_{k\in\mathbb Z} \Vert\Pi_kf\Vert. \end{align*} $$
$$ \begin{align*} \bigg\Vert \frac{1}{N}\sum_{n=0}^{N-1} T^nf-\Pi_{\mathcal M^\perp} f\bigg\Vert&=\bigg\Vert\frac{1}{\sqrt N}\sum_{j,k}\widehat f(j,k)\Psi_{j,k}(N)\bigg\Vert\\ &\leq \frac{1}{\sqrt N}\sum_{k\in\mathbb Z} \bigg\Vert\sum_{j\in\mathbb X}\widehat f(j,k) \Psi_{j,k}(N)\bigg\Vert\\ &= \frac{1}{\sqrt{N}} \sum_{k\in\mathbb Z} \bigg(\sum_{j\in\mathbb X}\vert\widehat f(j,k)\vert^2\bigg)^{\frac{1}{2}}= \frac{1}{\sqrt{N}} \sum_{k\in\mathbb Z} \Vert\Pi_kf\Vert. \end{align*} $$
Finally, observe that if
![]() $f=\Pi _{k}f$
for a single k, then all the above inequalities actually are identities. Hence, the theorem is sharp.
$f=\Pi _{k}f$
for a single k, then all the above inequalities actually are identities. Hence, the theorem is sharp.
The proof of Theorem 1.4 is in principle similar to the proof of Theorem 1.3. The main ingredient is the Rademacher–Menshov theorem, which we now recall.
Theorem 2.1 (Rademacher–Menshov)
There exists an absolute positive constant C such that for every positive measure space
![]() $ (X,\mu )$
and every orthogonal system
$ (X,\mu )$
and every orthogonal system
![]() $f_0, f_1 \dots $
in
$f_0, f_1 \dots $
in
![]() $L^2(X,\mu )$
, the maximal function
$L^2(X,\mu )$
, the maximal function
 $$\begin{align*}\mathcal{M}(x): = \sup_{ k \geq 0 } \bigg\vert \sum_{n=0}^k f_n(x) \bigg\vert \end{align*}$$
$$\begin{align*}\mathcal{M}(x): = \sup_{ k \geq 0 } \bigg\vert \sum_{n=0}^k f_n(x) \bigg\vert \end{align*}$$
satisfies the estimate
 $$\begin{align*}\Vert \mathcal{M} \Vert _{L^2(X,\mu)} \leq C \bigg( \sum_{n=0}^{+\infty} \log^2(n+2) \Vert f_n \Vert^2_{L^2(X,\mu)} \bigg)^{\frac{1}{2}}. \end{align*}$$
$$\begin{align*}\Vert \mathcal{M} \Vert _{L^2(X,\mu)} \leq C \bigg( \sum_{n=0}^{+\infty} \log^2(n+2) \Vert f_n \Vert^2_{L^2(X,\mu)} \bigg)^{\frac{1}{2}}. \end{align*}$$
It is important to emphasize that the constant C in the above theorem is absolute and we refer the reader to [Reference MeaneyMea07] for a discussion on this.
Recall also the next lemma by Kronecker, which is an application of Abel’s summation by parts formula.
Lemma 2.2 Suppose that
![]() $a_n$
is a sequence of complex numbers such that
$a_n$
is a sequence of complex numbers such that
![]() $\sum _{n=1}^\infty a_n$
, exists and is finite. Assume also that
$\sum _{n=1}^\infty a_n$
, exists and is finite. Assume also that
![]() $b_n$
is a nondecreasing sequence of positive numbers tending to infinity. Then,
$b_n$
is a nondecreasing sequence of positive numbers tending to infinity. Then,
 $$\begin{align*}\lim_{N \to \infty} \frac{1}{b_N} \sum_{n=0}^{N-1}b_n a_n = 0. \end{align*}$$
$$\begin{align*}\lim_{N \to \infty} \frac{1}{b_N} \sum_{n=0}^{N-1}b_n a_n = 0. \end{align*}$$
Proof of Theorem 1.4
We assume again that T is a bilateral shift. The proof for the unilateral case is the same. To simplify the notation, we also assume that f is in
![]() $\mathcal M$
, so that
$\mathcal M$
, so that
![]() $\Pi _{\mathcal M^\perp }f=0$
. Finally, assume that f has only finitely many nonzero Fourier coefficients. Then,
$\Pi _{\mathcal M^\perp }f=0$
. Finally, assume that f has only finitely many nonzero Fourier coefficients. Then,
 $$ \begin{align*} N\varepsilon(N)\bigg(\frac{1}{N} \sum_{n=0}^{N-1} T^{n}f(x)- \Pi_{\mathcal M^\perp}f(x)\bigg)= \varepsilon(N)\sum_{n=0}^{N-1} T^n f (x). \end{align*} $$
$$ \begin{align*} N\varepsilon(N)\bigg(\frac{1}{N} \sum_{n=0}^{N-1} T^{n}f(x)- \Pi_{\mathcal M^\perp}f(x)\bigg)= \varepsilon(N)\sum_{n=0}^{N-1} T^n f (x). \end{align*} $$
We derive both (1.1) and (1.3) from the boundedness of an auxiliary maximal function. Let
![]() $\varepsilon : [0,+\infty ) \to \mathbb {R}$
, not necessarily decreasing, and define
$\varepsilon : [0,+\infty ) \to \mathbb {R}$
, not necessarily decreasing, and define

We have
 $$ \begin{align*} \sum_{n=0}^{N-1} \varepsilon(n) T^n f(x)&=\sum_{n=0}^{N-1} \varepsilon(n) \sum_{j\in\mathbb X,k\in\mathbb Z}\widehat f(j,k)\varphi_{j,k+n}(x)= \sum_{k\in\mathbb Z} A(k)\sum_{n=0}^{N-1} \varepsilon(n)\Phi(k,n,x), \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{N-1} \varepsilon(n) T^n f(x)&=\sum_{n=0}^{N-1} \varepsilon(n) \sum_{j\in\mathbb X,k\in\mathbb Z}\widehat f(j,k)\varphi_{j,k+n}(x)= \sum_{k\in\mathbb Z} A(k)\sum_{n=0}^{N-1} \varepsilon(n)\Phi(k,n,x), \end{align*} $$
where we have set
 $$\begin{align*}A(k)=\Vert\Pi_k f\Vert_{L^2_\mu}=\bigg(\sum_{j\in\mathbb X}\vert\widehat f(j,k)\vert^2\bigg)^{\frac{1}{2}},\qquad\Phi(k,n,x)=\frac{1}{A(k)}\sum_{j\in\mathbb X}\widehat f(j,k)\varphi_{j,k+n}(x). \end{align*}$$
$$\begin{align*}A(k)=\Vert\Pi_k f\Vert_{L^2_\mu}=\bigg(\sum_{j\in\mathbb X}\vert\widehat f(j,k)\vert^2\bigg)^{\frac{1}{2}},\qquad\Phi(k,n,x)=\frac{1}{A(k)}\sum_{j\in\mathbb X}\widehat f(j,k)\varphi_{j,k+n}(x). \end{align*}$$
Then,
 $$ \begin{align*} \begin{split} \sup_{N\geq 1}\bigg\vert& \sum_{n=0}^{N-1} \varepsilon(n)T^n f (x)\bigg\vert= \sup_{N\geq 1}\bigg\vert\sum_{k\in\mathbb Z} A(k)\sum_{n=0}^{N-1} \varepsilon(n)\Phi(k,n,x)\bigg\vert. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \sup_{N\geq 1}\bigg\vert& \sum_{n=0}^{N-1} \varepsilon(n)T^n f (x)\bigg\vert= \sup_{N\geq 1}\bigg\vert\sum_{k\in\mathbb Z} A(k)\sum_{n=0}^{N-1} \varepsilon(n)\Phi(k,n,x)\bigg\vert. \end{split} \end{align*} $$
In the above formula, we simply omit the terms such that
![]() $A(k)=0$
. It may be promptly verified that
$A(k)=0$
. It may be promptly verified that
![]() $\{\Phi (k,n,x)\}_{n=0}^{N-1}$
is an orthonormal system for every fixed
$\{\Phi (k,n,x)\}_{n=0}^{N-1}$
is an orthonormal system for every fixed
![]() $k\in \mathbb Z$
and
$k\in \mathbb Z$
and
![]() $N\in \mathbb N$
. Hence, by means of the Rademacher–Menshov theorem,
$N\in \mathbb N$
. Hence, by means of the Rademacher–Menshov theorem,

Now a standard argument, as in [Reference ZygmundZyg03, p. 190], shows that inequality (2.1) with condition (1.2) implies that the series
![]() $\sum _{n=0}^\infty \varepsilon (n)T^nf(x)$
converges
$\sum _{n=0}^\infty \varepsilon (n)T^nf(x)$
converges
![]() $\mu $
-a.e. Moreover, restricting to a positive decreasing
$\mu $
-a.e. Moreover, restricting to a positive decreasing
![]() $\varepsilon $
, we apply Kronecker’s lemma with
$\varepsilon $
, we apply Kronecker’s lemma with
![]() $a_n= \varepsilon (n) T^nf(x)$
,
$a_n= \varepsilon (n) T^nf(x)$
,
![]() $ b_n =\varepsilon ^{-1}(n)$
and we have that
$ b_n =\varepsilon ^{-1}(n)$
and we have that
 $$\begin{align*}\lim_{N\to \infty} \varepsilon(N)\Big\vert \sum_{n=0}^{N-1}T^nf(x)\Big\vert = 0, \quad \mu \text{-a.e.,}\end{align*}$$
$$\begin{align*}\lim_{N\to \infty} \varepsilon(N)\Big\vert \sum_{n=0}^{N-1}T^nf(x)\Big\vert = 0, \quad \mu \text{-a.e.,}\end{align*}$$
which proves (1.3).
In order to prove (1.1), assume again that
![]() $\varepsilon $
is positive and decreasing. Then, by Abel’s summation by parts,
$\varepsilon $
is positive and decreasing. Then, by Abel’s summation by parts,
 $$ \begin{align*} \varepsilon(N)\sum_{n=0}^{N-1} T^nf(x)&= \frac{ \varepsilon(N)}{\varepsilon(N-1)}\sum_{n=0}^{N-1} \varepsilon(n) T^nf(x)\\ &\quad\quad- \varepsilon(N)\sum_{j=0}^{N-2}\bigg(\sum_{n=0}^{j}\varepsilon(n) T^nf(x)\bigg)\bigg(\frac{1}{\varepsilon(j+1)}-\frac{1}{\varepsilon(j)}\bigg). \end{align*} $$
$$ \begin{align*} \varepsilon(N)\sum_{n=0}^{N-1} T^nf(x)&= \frac{ \varepsilon(N)}{\varepsilon(N-1)}\sum_{n=0}^{N-1} \varepsilon(n) T^nf(x)\\ &\quad\quad- \varepsilon(N)\sum_{j=0}^{N-2}\bigg(\sum_{n=0}^{j}\varepsilon(n) T^nf(x)\bigg)\bigg(\frac{1}{\varepsilon(j+1)}-\frac{1}{\varepsilon(j)}\bigg). \end{align*} $$
Hence,

We conclude the section showing that the hypothesis of Theorem 1.4 are satisfied in the setting of Corollaries 1.5 and 1.6.
Proof of Corollary 1.5
One can verify that the composition operator
![]() $T_Bf(x,y)=f(B(x,y))$
is a bilateral shift with respect to the product Walsh system on the square
$T_Bf(x,y)=f(B(x,y))$
is a bilateral shift with respect to the product Walsh system on the square
![]() $[0,1)^2$
, whose definition we now recall. Let
$[0,1)^2$
, whose definition we now recall. Let
![]() $r_k$
be the one-dimensional kth Rademacher function
$r_k$
be the one-dimensional kth Rademacher function
On the unit square
![]() $[0,1)^2$
define the function
$[0,1)^2$
define the function
 $$\begin{align*}R_{k}(x,y):=\begin{cases} r_{k+1}(x) & k=0, 1,2,\ldots \\ r_{\vert k\vert}(y) & k=-1,-2,\ldots \end{cases} \end{align*}$$
$$\begin{align*}R_{k}(x,y):=\begin{cases} r_{k+1}(x) & k=0, 1,2,\ldots \\ r_{\vert k\vert}(y) & k=-1,-2,\ldots \end{cases} \end{align*}$$
and for every set of integers
![]() $k_1<k_2<\dots < k_n$
define
$k_1<k_2<\dots < k_n$
define
Then,
 $$\begin{align*}L^2_0([0,1)^2)=\overline{\operatorname*{\mathrm{span}}}\bigg\{W_{k_1k_2\dots k_n}: k_1<k_2<\dots<k_n, k_j\in\mathbb Z, n\in\mathbb N \bigg\}, \end{align*}$$
$$\begin{align*}L^2_0([0,1)^2)=\overline{\operatorname*{\mathrm{span}}}\bigg\{W_{k_1k_2\dots k_n}: k_1<k_2<\dots<k_n, k_j\in\mathbb Z, n\in\mathbb N \bigg\}, \end{align*}$$
where
![]() $L^2_0([0,1)^2)$
is the subspace of
$L^2_0([0,1)^2)$
is the subspace of
![]() $L^2([0,1)^2)$
consisting of functions with vanishing mean. One can verify that
$L^2([0,1)^2)$
consisting of functions with vanishing mean. One can verify that
Hence, the transformation T is a bilateral shift on
![]() $L^2_0([0,1)^2)$
with a generating wandering subspace given by
$L^2_0([0,1)^2)$
with a generating wandering subspace given by
 $$\begin{align*}\mathcal V= \overline{\operatorname*{\mathrm{span}}}\bigg\{W_{1 k_2\dots k_n}, 1<k_2<k_3<\dots k_n, k_j\in\mathbb Z, n\in\mathbb N\bigg\}. \end{align*}$$
$$\begin{align*}\mathcal V= \overline{\operatorname*{\mathrm{span}}}\bigg\{W_{1 k_2\dots k_n}, 1<k_2<k_3<\dots k_n, k_j\in\mathbb Z, n\in\mathbb N\bigg\}. \end{align*}$$
Then, Theorem 1.4 applies.
Proof of Corollary 1.6
Recall the definition of Laguerre polynomials
![]() $\{L_n\}_{n\in \mathbb N}$
,
$\{L_n\}_{n\in \mathbb N}$
,
 $$\begin{align*}L_n(x)=\frac{e^x}{n!}\frac{d^n}{dx^n}(e^{-x}x^n)=\sum_{k=0}^n \binom{n}{k}\frac{(-1)^k}{k!}x^k. \end{align*}$$
$$\begin{align*}L_n(x)=\frac{e^x}{n!}\frac{d^n}{dx^n}(e^{-x}x^n)=\sum_{k=0}^n \binom{n}{k}\frac{(-1)^k}{k!}x^k. \end{align*}$$
This family of polynomials is an orthonormal basis for the Hilbert space
![]() $L^2(\mathbb R_+, e^{-x} dx)$
. As observed by Von Neumann [Reference von NeumannvN29] (see also Brown and Halmos [Reference Brown, Halmos and ShieldsBHS65, p. 135]), the operator
$L^2(\mathbb R_+, e^{-x} dx)$
. As observed by Von Neumann [Reference von NeumannvN29] (see also Brown and Halmos [Reference Brown, Halmos and ShieldsBHS65, p. 135]), the operator
is the unilateral shift with respect to the Laguerre basis of
![]() $L^2(\mathbb R_+, e^{-x} dx)$
. Indeed,
$L^2(\mathbb R_+, e^{-x} dx)$
. Indeed,
 $$\begin{align*}TL_n(x)=\sum_{k=0}^n \binom{n}{k}\frac{(-1)^k}{k!}x^k+\sum_{k=0}^n \binom{n}{k}\frac{(-1)^{k+1}}{(k+1)!}x^{k+1}=\sum_{k=0}^{n+1} \binom{n+1}{k}\frac{(-1)^k}{k!}x^k=L_{n+1}(x).\end{align*}$$
$$\begin{align*}TL_n(x)=\sum_{k=0}^n \binom{n}{k}\frac{(-1)^k}{k!}x^k+\sum_{k=0}^n \binom{n}{k}\frac{(-1)^{k+1}}{(k+1)!}x^{k+1}=\sum_{k=0}^{n+1} \binom{n+1}{k}\frac{(-1)^k}{k!}x^k=L_{n+1}(x).\end{align*}$$
Hence, Theorem 1.4 applies.
3 Speed of convergence for toral endomorphisms
Before actually proving Theorem 1.7 and Corollary 1.8, we make some preliminary observations. If in Theorem 1.7, we choose a matrix A with
![]() $\vert \det A\vert>1$
, then the operator
$\vert \det A\vert>1$
, then the operator
![]() $T_A f= f\circ A$
is a unilateral shift on
$T_A f= f\circ A$
is a unilateral shift on
![]() $L^2_0(\mathbb T^2)$
, the space of square integrable functions with vanishing means. This is proved, e.g., in [Reference KrzyżewskiKrz93], but it will also follow from the proof of Lemma 3.3. If, on the other hand,
$L^2_0(\mathbb T^2)$
, the space of square integrable functions with vanishing means. This is proved, e.g., in [Reference KrzyżewskiKrz93], but it will also follow from the proof of Lemma 3.3. If, on the other hand,
![]() $\vert \det A\vert =1$
, then
$\vert \det A\vert =1$
, then
![]() $T_A$
is a bilateral shift on
$T_A$
is a bilateral shift on
![]() $L_0^2(\mathbb T^2)$
. A generating wandering subspace for
$L_0^2(\mathbb T^2)$
. A generating wandering subspace for
![]() $T_A$
can be constructed as follows. Let us consider equivalence relation on
$T_A$
can be constructed as follows. Let us consider equivalence relation on
![]() ${\mathbb {Z}}^2\setminus \{0\}$
defined by the orbits of
${\mathbb {Z}}^2\setminus \{0\}$
defined by the orbits of
![]() $A^*$
, i.e.,
$A^*$
, i.e.,
Let now
![]() $\mathcal E$
be the set containing of representative from each equivalence class of
$\mathcal E$
be the set containing of representative from each equivalence class of
![]() ${\mathbb {Z}}^2\setminus \{0\}/ \sim $
. A generating wandering subspace
${\mathbb {Z}}^2\setminus \{0\}/ \sim $
. A generating wandering subspace
![]() $\mathcal {V}_{\mathcal E}$
for
$\mathcal {V}_{\mathcal E}$
for
![]() $T_A$
is then given by
$T_A$
is then given by
The proof of Theorem 1.7 will follow from a series of preparatory results. In particular, we deal with the cases
![]() $\vert \det A\vert>1$
and
$\vert \det A\vert>1$
and
![]() $\vert \det A\vert =1$
in different ways. In this latter case, we will have to be more careful in constructing a generating wandering subspace
$\vert \det A\vert =1$
in different ways. In this latter case, we will have to be more careful in constructing a generating wandering subspace
![]() $\mathcal V_{\mathcal E}$
, which we recall is not unique for bilateral shifts.
$\mathcal V_{\mathcal E}$
, which we recall is not unique for bilateral shifts.
3.1 Proof of Theorem 1.7: case |det A| = 1
Let
![]() $\operatorname {\mathrm {tr}}(A)$
be the trace of the matrix A. Observe that if
$\operatorname {\mathrm {tr}}(A)$
be the trace of the matrix A. Observe that if
![]() $\det (A)=1$
the eigenvalues of A are given by
$\det (A)=1$
the eigenvalues of A are given by
 $$\begin{align*}\frac{\operatorname{\mathrm{tr}}(A)\pm \sqrt{\operatorname{\mathrm{tr}}^2(A)-4}}{2}. \end{align*}$$
$$\begin{align*}\frac{\operatorname{\mathrm{tr}}(A)\pm \sqrt{\operatorname{\mathrm{tr}}^2(A)-4}}{2}. \end{align*}$$
Since no eigenvalue of A is a root of unity by hypothesis, we can assume that
![]() ${\vert \operatorname {\mathrm {tr}}(A)\vert>2}$
. Otherwise, that is, if
${\vert \operatorname {\mathrm {tr}}(A)\vert>2}$
. Otherwise, that is, if
![]() $\operatorname {\mathrm {tr}}(A)=0,\pm 1,\pm 2$
, it can be checked by hand that the eigenvalues of A are roots of unity and in this case Birkhoff’s theorem would not apply since the matrix A would not be ergodic (see [Reference KrzyżewskiKrz93]). If
$\operatorname {\mathrm {tr}}(A)=0,\pm 1,\pm 2$
, it can be checked by hand that the eigenvalues of A are roots of unity and in this case Birkhoff’s theorem would not apply since the matrix A would not be ergodic (see [Reference KrzyżewskiKrz93]). If
![]() $\det (A)=-1$
, then the eigenvalues of A are given by
$\det (A)=-1$
, then the eigenvalues of A are given by
 $$\begin{align*}\frac{\operatorname{\mathrm{tr}}(A)\pm \sqrt{\operatorname{\mathrm{tr}}^2(A)+4}}{2}. \end{align*}$$
$$\begin{align*}\frac{\operatorname{\mathrm{tr}}(A)\pm \sqrt{\operatorname{\mathrm{tr}}^2(A)+4}}{2}. \end{align*}$$
Notice that these are roots of unity if and only if
![]() $\operatorname {\mathrm {tr}}(A)=0$
. In all remaining cases, we have two distinct eigenvalues
$\operatorname {\mathrm {tr}}(A)=0$
. In all remaining cases, we have two distinct eigenvalues
![]() $\lambda , \lambda ^{-1} \in \mathbb R $
and, without loss of generality, we can assume that
$\lambda , \lambda ^{-1} \in \mathbb R $
and, without loss of generality, we can assume that
![]() $0<\vert \lambda \vert ^{-1}<1<\vert \lambda \vert $
. We now take advantage of this to define a suitable generating wandering subspace for the bilateral shift
$0<\vert \lambda \vert ^{-1}<1<\vert \lambda \vert $
. We now take advantage of this to define a suitable generating wandering subspace for the bilateral shift
![]() $T_A$
. Let
$T_A$
. Let
![]() $S\in \operatorname {\mathrm {GL}}_2(\mathbb R)$
be such that
$S\in \operatorname {\mathrm {GL}}_2(\mathbb R)$
be such that
 $$\begin{align*}A = S^{-1} \begin{bmatrix} \lambda^{-1} & 0 \\ 0 & \lambda \end{bmatrix} S= S^{-1}DS. \end{align*}$$
$$\begin{align*}A = S^{-1} \begin{bmatrix} \lambda^{-1} & 0 \\ 0 & \lambda \end{bmatrix} S= S^{-1}DS. \end{align*}$$
Let
![]() $\mathcal E\subseteq {\mathbb {Z}}^2\backslash \{0\}$
be such that it contains exactly one element from each orbit of the action of A on
$\mathcal E\subseteq {\mathbb {Z}}^2\backslash \{0\}$
be such that it contains exactly one element from each orbit of the action of A on
![]() ${\mathbb {Z}}^2$
. We choose such element as follows. Define
${\mathbb {Z}}^2$
. We choose such element as follows. Define
![]() $\vert \xi \vert _{\infty }=\vert (\xi _1,\xi _2)\vert _{\infty }=\max \{\vert \xi _1\vert ,\vert \xi _2\vert \}$
. Let
$\vert \xi \vert _{\infty }=\vert (\xi _1,\xi _2)\vert _{\infty }=\max \{\vert \xi _1\vert ,\vert \xi _2\vert \}$
. Let
![]() $\mathcal O$
an orbit of A in
$\mathcal O$
an orbit of A in
![]() $\mathbb {Z}^2\setminus \{ 0\}$
and consider the set
$\mathbb {Z}^2\setminus \{ 0\}$
and consider the set
![]() $S \mathcal {O}$
. Then, we choose
$S \mathcal {O}$
. Then, we choose
![]() $\xi \in \mathcal {O} $
such that
$\xi \in \mathcal {O} $
such that
![]() $S\xi $
has the minimal
$S\xi $
has the minimal
![]() $ \vert \cdot \vert _{\infty } $
norm. Equivalently, for all
$ \vert \cdot \vert _{\infty } $
norm. Equivalently, for all
![]() $k\in \mathbb Z$
, we have that
$k\in \mathbb Z$
, we have that
Then, a generating wandering subspace for
![]() $T_A$
is defined as in (3.1).
$T_A$
is defined as in (3.1).
Using the notation above, we prove the following.
Lemma 3.1 Let A be a
![]() $2\times 2$
integer matrix such that
$2\times 2$
integer matrix such that
![]() $\vert \det A\vert =1$
and no eigenvalues of A is a root of unity. Let
$\vert \det A\vert =1$
and no eigenvalues of A is a root of unity. Let
![]() $\mathcal E$
be defined as above. Then, there exist constants
$\mathcal E$
be defined as above. Then, there exist constants
![]() $c>0$
and
$c>0$
and
![]() $q>1$
such that, for every
$q>1$
such that, for every
![]() $k\in \mathbb Z$
,
$k\in \mathbb Z$
,
Proof Assume that
![]() $\det A=1$
; the case
$\det A=1$
; the case
![]() $\det A=-1$
is similar. Since for every
$\det A=-1$
is similar. Since for every
![]() ${\xi \in {\mathbb {Z}}^2\setminus \{ 0 \}}$
and
${\xi \in {\mathbb {Z}}^2\setminus \{ 0 \}}$
and
![]() $k\in \mathbb Z$
it holds that
$k\in \mathbb Z$
it holds that
and all norms in a finite-dimensional vector space are equivalent, it suffices to show that there exist
![]() $c>0$
,
$c>0$
,
![]() $q>1$
such that
$q>1$
such that
![]() $| D^{k}S\xi \vert _{\infty }\geq cq ^{|k| }$
for every
$| D^{k}S\xi \vert _{\infty }\geq cq ^{|k| }$
for every
![]() $\xi \in \mathcal E $
. Let
$\xi \in \mathcal E $
. Let
![]() $\eta =(\eta _1,\eta _2)=S\xi $
where
$\eta =(\eta _1,\eta _2)=S\xi $
where
![]() $\xi $
is in
$\xi $
is in
![]() $\mathcal E$
and let
$\mathcal E$
and let
![]() $\lambda ^{-1},\lambda $
the two real eigenvalues of A with
$\lambda ^{-1},\lambda $
the two real eigenvalues of A with
![]() $|\lambda |>1$
. Then,
$|\lambda |>1$
. Then,
and, similarly,
Hence,
The conclusion will follows once we prove that
![]() $\min \{|\eta _1|,|\eta _2|\}$
is bounded from below uniformly for
$\min \{|\eta _1|,|\eta _2|\}$
is bounded from below uniformly for
![]() $\eta =(\eta _1,\eta _2)$
in
$\eta =(\eta _1,\eta _2)$
in
![]() $\mathcal E$
. But this is true because of the following. If
$\mathcal E$
. But this is true because of the following. If
![]() $|\eta _2|\leq |\eta _1|$
, by the definition of
$|\eta _2|\leq |\eta _1|$
, by the definition of
![]() $\mathcal E$
,
$\mathcal E$
,
The last identity holds since if
![]() $\left \vert \left ( \lambda ^{-1}\eta _{1},\lambda \eta _{2}\right ) \right \vert _{\infty }=|\lambda ^{-1}||\eta _1|$
, then we would have
$\left \vert \left ( \lambda ^{-1}\eta _{1},\lambda \eta _{2}\right ) \right \vert _{\infty }=|\lambda ^{-1}||\eta _1|$
, then we would have
![]() ${|\eta _1|\leq |\lambda ^{-1}||\eta _1|}$
, which is a contradiction since
${|\eta _1|\leq |\lambda ^{-1}||\eta _1|}$
, which is a contradiction since
![]() $|\lambda ^{-1}|<1$
and
$|\lambda ^{-1}|<1$
and
![]() $\eta _1 \neq 0$
. Similarly, if
$\eta _1 \neq 0$
. Similarly, if
![]() $\left \vert \eta _{1}\right \vert \leq \left \vert \eta _{2}\right \vert $
,
$\left \vert \eta _{1}\right \vert \leq \left \vert \eta _{2}\right \vert $
,
Hence,
![]() $|(\eta _1,\eta _2)\vert _{\infty }\leq |\lambda | \min \{|\eta _1|,|\eta _2|\}$
, that is,
$|(\eta _1,\eta _2)\vert _{\infty }\leq |\lambda | \min \{|\eta _1|,|\eta _2|\}$
, that is,
![]() $|\eta _1|$
and
$|\eta _1|$
and
![]() $|\eta _2|$
are comparable. Therefore, by (3.3),
$|\eta _2|$
are comparable. Therefore, by (3.3),
for some positive constant c. This follows from the fact that
![]() $\eta \in S{\mathbb {Z}}^2\backslash \{0\}$
.
$\eta \in S{\mathbb {Z}}^2\backslash \{0\}$
.
We now conclude the proof of Theorem 1.7 in the case
![]() $|\det A|=1$
. As observed at the beginning of Section 3, the operator
$|\det A|=1$
. As observed at the beginning of Section 3, the operator
![]() $T_A f(x)=f(Ax)$
is a bilateral shift on
$T_A f(x)=f(Ax)$
is a bilateral shift on
![]() $L^2_0(\mathbb T^2)$
with a generating subspace given by
$L^2_0(\mathbb T^2)$
with a generating subspace given by
![]() $\mathcal V_{\mathcal E}$
as in (3.1) where
$\mathcal V_{\mathcal E}$
as in (3.1) where
![]() $\mathcal E$
is defined by means of the property (3.2). Hence, Theorem 1.4 applies and, in particular, it applies with
$\mathcal E$
is defined by means of the property (3.2). Hence, Theorem 1.4 applies and, in particular, it applies with
![]() $\varepsilon (n)=(n+1)^{-\frac {1}{2}}(\log (2+n))^{-\frac {3}{2}- \eta }$
for any
$\varepsilon (n)=(n+1)^{-\frac {1}{2}}(\log (2+n))^{-\frac {3}{2}- \eta }$
for any
![]() $\eta>0$
.
$\eta>0$
.
Set now
![]() $\mathcal {F}_k :=(A^{*})^k\mathcal E$
. Observe that A satisfies the hypothesis of Lemma 3.1 if and only if
$\mathcal {F}_k :=(A^{*})^k\mathcal E$
. Observe that A satisfies the hypothesis of Lemma 3.1 if and only if
![]() $A^*$
does. Hence, by such lemma, there exist constants
$A^*$
does. Hence, by such lemma, there exist constants
![]() $c>0$
and
$c>0$
and
![]() $q>1$
such that, for every
$q>1$
such that, for every
![]() $k\in \mathbb Z$
,
$k\in \mathbb Z$
,
Hence, for every positive increasing function
![]() $\nu $
and f satisfying (1.4), one has
$\nu $
and f satisfying (1.4), one has
 $$ \begin{align*} \sum_{k\in\mathbb Z \cup \{ 0\} }\Vert\Pi_k f\Vert_{L^2}&=\sum_{k\in\mathbb Z \cup \{ 0\}}\bigg(\sum_{\xi \in \mathcal F_k } |\widehat f(\xi)|^2\bigg)^{\frac{1}{2}}\\ &\leq\bigg(\sum_{k\in\mathbb Z \cup \{ 0\}} \nu^{-2}(k)\bigg)^{\frac{1}{2}}\bigg(\sum_{k\in\mathbb Z \cup \{ 0\}}\nu^2(k)\sum_{\xi \in \mathcal{F}_k}|\widehat f(\xi)|^2\bigg)^{\frac{1}{2}} \\ &\leq \bigg(\sum_{k\in\mathbb Z \cup \{ 0\}} \nu^{-2}(k)\bigg)^{\frac{1}{2}} \bigg(\sum_{k\in\mathbb Z \cup \{ 0\}}\sum_{\xi \in \mathcal{F}_k} \nu^2\Big( \frac{\log |\xi| - \log c}{\log q } \Big) |\widehat f(\xi)|^2\bigg)^{\frac{1}{2}}. \end{align*} $$
$$ \begin{align*} \sum_{k\in\mathbb Z \cup \{ 0\} }\Vert\Pi_k f\Vert_{L^2}&=\sum_{k\in\mathbb Z \cup \{ 0\}}\bigg(\sum_{\xi \in \mathcal F_k } |\widehat f(\xi)|^2\bigg)^{\frac{1}{2}}\\ &\leq\bigg(\sum_{k\in\mathbb Z \cup \{ 0\}} \nu^{-2}(k)\bigg)^{\frac{1}{2}}\bigg(\sum_{k\in\mathbb Z \cup \{ 0\}}\nu^2(k)\sum_{\xi \in \mathcal{F}_k}|\widehat f(\xi)|^2\bigg)^{\frac{1}{2}} \\ &\leq \bigg(\sum_{k\in\mathbb Z \cup \{ 0\}} \nu^{-2}(k)\bigg)^{\frac{1}{2}} \bigg(\sum_{k\in\mathbb Z \cup \{ 0\}}\sum_{\xi \in \mathcal{F}_k} \nu^2\Big( \frac{\log |\xi| - \log c}{\log q } \Big) |\widehat f(\xi)|^2\bigg)^{\frac{1}{2}}. \end{align*} $$
The conclusion follows choosing
![]() $\nu (t)=t^{\frac {1}{2}+\frac \delta 2}+1$
.
$\nu (t)=t^{\frac {1}{2}+\frac \delta 2}+1$
.
3.2 Proof of Theorem 1.7: case |det A| > 1
We want to prove the analogous of Lemma 3.1 for a matrix A with
![]() $|\det A|>1$
. However, we need a preliminary result, which is a special case of [Reference KatznelsonKat71, Lemma 3]. The proof we provide here for the reader’s convenience is essentially the same one as in [Reference KatznelsonKat71] adapted to the case
$|\det A|>1$
. However, we need a preliminary result, which is a special case of [Reference KatznelsonKat71, Lemma 3]. The proof we provide here for the reader’s convenience is essentially the same one as in [Reference KatznelsonKat71] adapted to the case
![]() $d=2$
.
$d=2$
.
Lemma 3.2 Let A be a
![]() $2\times 2$
integer matrix with a real irrational eigenvalue
$2\times 2$
integer matrix with a real irrational eigenvalue
![]() $\lambda ,$
and let
$\lambda ,$
and let
![]() $V_\lambda $
be its corresponding eigenspace. Then, there exists
$V_\lambda $
be its corresponding eigenspace. Then, there exists
![]() $C_A> 0 $
such that, for
$C_A> 0 $
such that, for
![]() $\xi \in {\mathbb {Z}}^2 \setminus \{0\}$
,
$\xi \in {\mathbb {Z}}^2 \setminus \{0\}$
,
where
![]() $\operatorname {\mathrm {dist}}$
is the Euclidean distance between
$\operatorname {\mathrm {dist}}$
is the Euclidean distance between
![]() $\xi $
and
$\xi $
and
![]() $V_\lambda .$
$V_\lambda .$
Proof By Dirichlet’s theorem, for every
![]() $Q\in \mathbb N$
, there exists
$Q\in \mathbb N$
, there exists
![]() $q \in \mathbb N,q\leq Q$
and
$q \in \mathbb N,q\leq Q$
and
![]() $r\in \mathbb Z$
such that
$r\in \mathbb Z$
such that
Now, fix
![]() $\xi \in {\mathbb {Z}}^2\setminus \{0 \}$
and notice that
$\xi \in {\mathbb {Z}}^2\setminus \{0 \}$
and notice that
![]() $ (q A-r)\xi \in {\mathbb {Z}}^2 \setminus \{0\}$
, so
$ (q A-r)\xi \in {\mathbb {Z}}^2 \setminus \{0\}$
, so
![]() $ 1/q \leq \vert (A- r/q)\xi \vert $
. Let y be the orthogonal projection of
$ 1/q \leq \vert (A- r/q)\xi \vert $
. Let y be the orthogonal projection of
![]() $\xi $
on
$\xi $
on
![]() $V_\lambda $
. We have
$V_\lambda $
. We have
 $$ \begin{align*} \frac{1}{q} \leq & \Big \vert \Big(A-\frac{r}{q}\Big)\xi \Big\vert = \Big\vert \Big(A-\frac rq \Big) (\xi-y) + \Big(\lambda-\frac rq \Big) y \Big\vert \\ \leq & (\Vert A \Vert + |\lambda|+1 ) \operatorname{\mathrm{dist}}(\xi,V_\lambda) + \frac{\vert \xi \vert}{ q Q }. \end{align*} $$
$$ \begin{align*} \frac{1}{q} \leq & \Big \vert \Big(A-\frac{r}{q}\Big)\xi \Big\vert = \Big\vert \Big(A-\frac rq \Big) (\xi-y) + \Big(\lambda-\frac rq \Big) y \Big\vert \\ \leq & (\Vert A \Vert + |\lambda|+1 ) \operatorname{\mathrm{dist}}(\xi,V_\lambda) + \frac{\vert \xi \vert}{ q Q }. \end{align*} $$
Setting
![]() $C = \Vert A \Vert + |\lambda | +1 $
and rearranging the above inequality, we get
$C = \Vert A \Vert + |\lambda | +1 $
and rearranging the above inequality, we get
Setting
![]() $Q = \lceil 2 \vert \xi \vert \rceil $
we obtain the desired estimate.
$Q = \lceil 2 \vert \xi \vert \rceil $
we obtain the desired estimate.
Lemma 3.3 Let A be a
![]() $2\times 2$
integer matrix such that
$2\times 2$
integer matrix such that
![]() $|\det A|>1$
and no eigenvalue of A is a root of unity. Then, there exist constants
$|\det A|>1$
and no eigenvalue of A is a root of unity. Then, there exist constants
![]() $c>0$
and
$c>0$
and
![]() $q>1$
such that, for every
$q>1$
such that, for every
![]() $k\in \mathbb N$
$k\in \mathbb N$
Proof We study separately the cases when A is diagonalizable and when it is not. Denote by
![]() $\lambda , \Lambda \in \mathbb C$
the eigenvalues of the matrix A so that
$\lambda , \Lambda \in \mathbb C$
the eigenvalues of the matrix A so that
![]() $|\lambda | \leq |\Lambda |$
. Recall that
$|\lambda | \leq |\Lambda |$
. Recall that
![]() $\det (A)=\lambda \Lambda $
is an integer different from
$\det (A)=\lambda \Lambda $
is an integer different from
![]() $-1,1,0$
. If these eigenvalues are complex, then they are conjugate to each other and
$-1,1,0$
. If these eigenvalues are complex, then they are conjugate to each other and
![]() $1<|\lambda | = |\Lambda |$
. If the eigenvalues are real, then, either
$1<|\lambda | = |\Lambda |$
. If the eigenvalues are real, then, either
![]() $1<|\lambda |\leq |\Lambda | $
or
$1<|\lambda |\leq |\Lambda | $
or
![]() $|\lambda |<1<|\Lambda |$
. In this last case,
$|\lambda |<1<|\Lambda |$
. In this last case,
![]() $\lambda $
and
$\lambda $
and
![]() $\Lambda $
cannot be rational, since the characteristic polynomial of A is a monic polynomial with integer coefficients and any rational root of such polynomial is an integer.
$\Lambda $
cannot be rational, since the characteristic polynomial of A is a monic polynomial with integer coefficients and any rational root of such polynomial is an integer.
A is diagonalizable and 1 < |λ|≤|Λ|. In this case, there exists
![]() $S\in \operatorname {\mathrm {GL}}_2(\mathbb C)$
such that for every
$S\in \operatorname {\mathrm {GL}}_2(\mathbb C)$
such that for every
![]() $k\in \mathbb N$
$k\in \mathbb N$
 $$\begin{align*}A^k = S^{-1} \begin{bmatrix} \lambda^k & 0 \\ 0 & \Lambda^k \end{bmatrix} S. \end{align*}$$
$$\begin{align*}A^k = S^{-1} \begin{bmatrix} \lambda^k & 0 \\ 0 & \Lambda^k \end{bmatrix} S. \end{align*}$$
Therefore, for
![]() $\xi \in {\mathbb {Z}}^2\setminus \{0\}$
,
$\xi \in {\mathbb {Z}}^2\setminus \{0\}$
,
 $$\begin{align*}\vert A^k \xi \vert \geq \frac{1}{\Vert S \Vert} \Bigg| \begin{bmatrix} \lambda^k & 0 \\ 0 & \Lambda^k \end{bmatrix} S \xi \Bigg| \geq \frac{ |\lambda |^{k} |\xi|}{ \Vert S\Vert \, \Vert S^{-1} \Vert} \geq \frac{ |\lambda |^{k}}{ \Vert S\Vert \, \Vert S^{-1} \Vert} , \end{align*}$$
$$\begin{align*}\vert A^k \xi \vert \geq \frac{1}{\Vert S \Vert} \Bigg| \begin{bmatrix} \lambda^k & 0 \\ 0 & \Lambda^k \end{bmatrix} S \xi \Bigg| \geq \frac{ |\lambda |^{k} |\xi|}{ \Vert S\Vert \, \Vert S^{-1} \Vert} \geq \frac{ |\lambda |^{k}}{ \Vert S\Vert \, \Vert S^{-1} \Vert} , \end{align*}$$
and the claim is proved in this case.
A is diagonalizable and |λ| < 1 < |Λ|. Let
![]() $V_\lambda , V_\Lambda $
be the one-dimensional eigen spaces corresponding to
$V_\lambda , V_\Lambda $
be the one-dimensional eigen spaces corresponding to
![]() $\lambda $
and
$\lambda $
and
![]() $\Lambda $
, respectively, let
$\Lambda $
, respectively, let
![]() $\theta \in (0,\pi )$
be the angle between them, and let
$\theta \in (0,\pi )$
be the angle between them, and let
![]() $P_\lambda , P_\Lambda $
be the oblique projections with respect to the axes
$P_\lambda , P_\Lambda $
be the oblique projections with respect to the axes
![]() $V_\lambda , V_\Lambda $
. Define a new norm in
$V_\lambda , V_\Lambda $
. Define a new norm in
![]() ${\mathbb {R}}^2$
as follows,
${\mathbb {R}}^2$
as follows,
This is of course equivalent to the Euclidean norm of
![]() ${\mathbb {R}}^2$
up to multiplicative constants which depends on A. In what follows
${\mathbb {R}}^2$
up to multiplicative constants which depends on A. In what follows
![]() $c, C$
denote positive constants which depend only on A and might change from appearance to appearance. Applying now Lemma 3.2 for some
$c, C$
denote positive constants which depend only on A and might change from appearance to appearance. Applying now Lemma 3.2 for some
![]() $\xi \in {\mathbb {Z}}^2 \setminus \{0\}$
, we have
$\xi \in {\mathbb {Z}}^2 \setminus \{0\}$
, we have
Hence,
Writing
![]() $\xi = P_\lambda \xi + P_\Lambda \xi $
and applying
$\xi = P_\lambda \xi + P_\Lambda \xi $
and applying
![]() $A^k$
, we obtain
$A^k$
, we obtain
![]() $A^k \xi = \lambda ^k P_\lambda \xi + \Lambda ^k P_\Lambda \xi $
. Hence,
$A^k \xi = \lambda ^k P_\lambda \xi + \Lambda ^k P_\Lambda \xi $
. Hence,
 $$ \begin{align*} C \vert A^k \xi \vert \geq [A^kx]_A & = |\lambda|^k \vert P_\lambda \xi \vert + |\Lambda|^k \vert P_\Lambda \xi \vert \\[0.6em] & = |\lambda|^k( [\xi]_A - \vert P_\Lambda \xi\vert ) + |\Lambda|^k \vert P_\Lambda \xi \vert \\[0.6em] & = |\lambda|^k [\xi]_A + (|\Lambda|^k-|\lambda|^k) \vert P_\Lambda \xi \vert \\[0.5em] & \geq |\lambda|^k [\xi]_A + c \frac{|\Lambda|^k-|\lambda|^k}{[\xi]_A} =: f([\xi]_A), \end{align*} $$
$$ \begin{align*} C \vert A^k \xi \vert \geq [A^kx]_A & = |\lambda|^k \vert P_\lambda \xi \vert + |\Lambda|^k \vert P_\Lambda \xi \vert \\[0.6em] & = |\lambda|^k( [\xi]_A - \vert P_\Lambda \xi\vert ) + |\Lambda|^k \vert P_\Lambda \xi \vert \\[0.6em] & = |\lambda|^k [\xi]_A + (|\Lambda|^k-|\lambda|^k) \vert P_\Lambda \xi \vert \\[0.5em] & \geq |\lambda|^k [\xi]_A + c \frac{|\Lambda|^k-|\lambda|^k}{[\xi]_A} =: f([\xi]_A), \end{align*} $$
where
![]() $f(t)=|\lambda |^k t + c(|\Lambda |^k-|\lambda |^k) t^{-1}, t>0$
. Such function f admits a global minimum at
$f(t)=|\lambda |^k t + c(|\Lambda |^k-|\lambda |^k) t^{-1}, t>0$
. Such function f admits a global minimum at
![]() $t_{\min }$
,
$t_{\min }$
,
 $$\begin{align*}t_{\min} = \sqrt{\frac{c(|\Lambda|^k - |\lambda|^k)}{|\lambda|^k}}, \quad f(t_{\min}) = 2 \sqrt{ c |\lambda|^k (|\Lambda|^k - |\lambda|^k)}. \end{align*}$$
$$\begin{align*}t_{\min} = \sqrt{\frac{c(|\Lambda|^k - |\lambda|^k)}{|\lambda|^k}}, \quad f(t_{\min}) = 2 \sqrt{ c |\lambda|^k (|\Lambda|^k - |\lambda|^k)}. \end{align*}$$
For k sufficiently large the estimate
![]() $f(t_{\min }) \geq c \sqrt {|\lambda |^k | \Lambda |^k} = c |\det (A)|^{\frac {k}{2}} $
holds true, and this, combined with the above estimate, proves the claim.
$f(t_{\min }) \geq c \sqrt {|\lambda |^k | \Lambda |^k} = c |\det (A)|^{\frac {k}{2}} $
holds true, and this, combined with the above estimate, proves the claim.
A is not diagonalizable
. In this case, we have a single eigenvalue
![]() $\lambda $
with
$\lambda $
with
![]() $2 \lambda = \operatorname {\mathrm {tr}}(A)$
and
$2 \lambda = \operatorname {\mathrm {tr}}(A)$
and
![]() $\lambda ^2=\det (A)$
. Hence,
$\lambda ^2=\det (A)$
. Hence,
![]() $\operatorname {\mathrm {tr}}(A)^2=4\det (A)$
. This implies that
$\operatorname {\mathrm {tr}}(A)^2=4\det (A)$
. This implies that
![]() $\operatorname {\mathrm {tr}}(A)$
is an even integer, so that
$\operatorname {\mathrm {tr}}(A)$
is an even integer, so that
![]() $\lambda \in \mathbb {Z}\setminus \{0\}$
. The Jordan decomposition of A guarantees that
$\lambda \in \mathbb {Z}\setminus \{0\}$
. The Jordan decomposition of A guarantees that
 $$\begin{align*}A= S^{-1}\begin{bmatrix} \lambda & 1 \\ 0 & \lambda \end{bmatrix} S, \end{align*}$$
$$\begin{align*}A= S^{-1}\begin{bmatrix} \lambda & 1 \\ 0 & \lambda \end{bmatrix} S, \end{align*}$$
for some
![]() $S\in \operatorname {\mathrm {GL}}_2(\mathbb C)$
. However, since the columns of S are obtained by solving a homogeneous system of linear equations with integer coefficients, we can assume, without loss of generality, that S has integer entries. Assume for the moment that
$S\in \operatorname {\mathrm {GL}}_2(\mathbb C)$
. However, since the columns of S are obtained by solving a homogeneous system of linear equations with integer coefficients, we can assume, without loss of generality, that S has integer entries. Assume for the moment that
![]() $\lambda | k$
, i.e., there exists
$\lambda | k$
, i.e., there exists
![]() $q\in \mathbb Z$
such that
$q\in \mathbb Z$
such that
![]() $k=q \lambda $
. Then,
$k=q \lambda $
. Then,
 $$ \begin{align*} A^k = S^{-1} \begin{bmatrix} \lambda^ k & k \lambda^{k-1} \\ 0 & \lambda^k \end{bmatrix} S = \lambda^k S^{-1} \begin{bmatrix} 1 & q \\ 0 & 1 \end{bmatrix} S. \end{align*} $$
$$ \begin{align*} A^k = S^{-1} \begin{bmatrix} \lambda^ k & k \lambda^{k-1} \\ 0 & \lambda^k \end{bmatrix} S = \lambda^k S^{-1} \begin{bmatrix} 1 & q \\ 0 & 1 \end{bmatrix} S. \end{align*} $$
Notice that
 $ U: = \begin {bmatrix} 1 & q \\ 0 & 1 \end {bmatrix}$
is in
$ U: = \begin {bmatrix} 1 & q \\ 0 & 1 \end {bmatrix}$
is in
![]() $GL_2(\mathbb Z)$
. Therefore,
$GL_2(\mathbb Z)$
. Therefore,
In particular, it follows that
which proves the claim when
![]() $\lambda | k$
. In general, let
$\lambda | k$
. In general, let
![]() $k\equiv r\mod |\lambda |, 0\leq r < |\lambda |$
. Then,
$k\equiv r\mod |\lambda |, 0\leq r < |\lambda |$
. Then,
![]() ${\delta _n \geq \delta _{k-r} \geq c |\lambda |^{k-r} \geq (c |\lambda |^{-|\lambda |}) |\det (A)|^{\frac {k}{2}}}$
, and this concludes the proof for a nondiagonalizable matrix A.
${\delta _n \geq \delta _{k-r} \geq c |\lambda |^{k-r} \geq (c |\lambda |^{-|\lambda |}) |\det (A)|^{\frac {k}{2}}}$
, and this concludes the proof for a nondiagonalizable matrix A.
We now conclude the proof of Theorem 1.7 in the case
![]() $|\det A|>1$
. Notice that A satisfies the hypothesis of Lemma 3.3 if and only if
$|\det A|>1$
. Notice that A satisfies the hypothesis of Lemma 3.3 if and only if
![]() $A^*$
does. By Wold’s theorem, the unitary part of the operator
$A^*$
does. By Wold’s theorem, the unitary part of the operator
![]() $T_A f = f\circ A$
acts on the subspace
$T_A f = f\circ A$
acts on the subspace
![]() $\bigcap _{k\in \mathbb N\cup \{0\}} T^k_A(L_0^2(\mathbb T^2))$
, but this intersection is trivial and this follows at once from the fact that
$\bigcap _{k\in \mathbb N\cup \{0\}} T^k_A(L_0^2(\mathbb T^2))$
, but this intersection is trivial and this follows at once from the fact that
![]() $ \bigcap _{k\in \mathbb N\cup \{0\}} (A^*)^{k}{\mathbb {Z}}^2 =\{ 0\} $
since
$ \bigcap _{k\in \mathbb N\cup \{0\}} (A^*)^{k}{\mathbb {Z}}^2 =\{ 0\} $
since
by Lemma 3.3 applied to
![]() $A^*$
. Therefore,
$A^*$
. Therefore,
![]() $T_A$
is a unilateral shift with generating wandering subspace
$T_A$
is a unilateral shift with generating wandering subspace
Hence, Theorem 1.4 applies and, in particular, it applies with
![]() $\varepsilon (n)=(n+1)^{-\frac {1}{2}}(\log (2+n))^{-\frac {3}{2}- \eta }$
for any
$\varepsilon (n)=(n+1)^{-\frac {1}{2}}(\log (2+n))^{-\frac {3}{2}- \eta }$
for any
![]() $\eta>0$
. The proof now proceeds as in the case of matrices with determinant
$\eta>0$
. The proof now proceeds as in the case of matrices with determinant
![]() $\pm 1$
. Set
$\pm 1$
. Set
![]() $\mathcal {F}_k :=A^{*k}{\mathbb {Z}}^2 \setminus A^{*(k+1)}{\mathbb {Z}}^2$
. By Lemma (3.3) applied to
$\mathcal {F}_k :=A^{*k}{\mathbb {Z}}^2 \setminus A^{*(k+1)}{\mathbb {Z}}^2$
. By Lemma (3.3) applied to
![]() $A^*$
, for every positive increasing function
$A^*$
, for every positive increasing function
![]() $\nu $
and f satisfying (1.4), one has
$\nu $
and f satisfying (1.4), one has
 $$ \begin{align*} \sum_{k\in\mathbb N \cup \{ 0\} }\Vert\Pi_k f\Vert_{L^2}&=\sum_{k\in\mathbb N \cup \{ 0\}}\bigg(\sum_{\xi \in \mathcal F_k } |\widehat f(\xi)|^2\bigg)^{\frac{1}{2}}\\ &\leq\bigg(\sum_{k\in\mathbb N \cup \{ 0\}} \nu^{-2}(k)\bigg)^{\frac{1}{2}}\bigg(\sum_{k\in\mathbb N \cup \{ 0\}}\nu^2(k)\sum_{\xi \in \mathcal{F}_k}|\widehat f(\xi)|^2\bigg)^{\frac{1}{2}} \\ &\leq \bigg(\sum_{k\in\mathbb N \cup \{ 0\}} \nu^{-2}(k)\bigg)^{\frac{1}{2}} \bigg(\sum_{k\in\mathbb N \cup \{ 0\}}\sum_{\xi \in \mathcal{F}_k} \nu^2\Big( \frac{\log |\xi| - \log c}{\log q } \Big) |\widehat f(\xi)|^2\bigg)^{\frac{1}{2}}. \end{align*} $$
$$ \begin{align*} \sum_{k\in\mathbb N \cup \{ 0\} }\Vert\Pi_k f\Vert_{L^2}&=\sum_{k\in\mathbb N \cup \{ 0\}}\bigg(\sum_{\xi \in \mathcal F_k } |\widehat f(\xi)|^2\bigg)^{\frac{1}{2}}\\ &\leq\bigg(\sum_{k\in\mathbb N \cup \{ 0\}} \nu^{-2}(k)\bigg)^{\frac{1}{2}}\bigg(\sum_{k\in\mathbb N \cup \{ 0\}}\nu^2(k)\sum_{\xi \in \mathcal{F}_k}|\widehat f(\xi)|^2\bigg)^{\frac{1}{2}} \\ &\leq \bigg(\sum_{k\in\mathbb N \cup \{ 0\}} \nu^{-2}(k)\bigg)^{\frac{1}{2}} \bigg(\sum_{k\in\mathbb N \cup \{ 0\}}\sum_{\xi \in \mathcal{F}_k} \nu^2\Big( \frac{\log |\xi| - \log c}{\log q } \Big) |\widehat f(\xi)|^2\bigg)^{\frac{1}{2}}. \end{align*} $$
The conclusion follows choosing
![]() $\nu (t)=t^{\frac {1}{2}+\frac {\delta }{2}}+1$
. In only remains to prove Corollary 1.8, but this is now immediate.
$\nu (t)=t^{\frac {1}{2}+\frac {\delta }{2}}+1$
. In only remains to prove Corollary 1.8, but this is now immediate.
4 Concluding remarks
As mentioned in the introduction, functions satisfying condition (1.4) on their Fourier coefficients are, for instance, functions in any fractional Sobolev space. Here is another, more general, sufficient condition in terms of the
![]() $L^2$
integral modulus of continuity.
$L^2$
integral modulus of continuity.
Proposition 4.1 Let
![]() $\omega (f,t) , t>0$
, be the modulus of continuity of the function
$\omega (f,t) , t>0$
, be the modulus of continuity of the function
![]() ${f \in L^{2}(\mathbb {T}^{d})} $
,
${f \in L^{2}(\mathbb {T}^{d})} $
,
 $$\begin{align*}\omega (f,t):= \sup_{| y| \leq t}\Big( \int_{ \mathbb{T}^{d}}| f(x+y)-f(x)| ^{2}dx\Big) ^{\frac{1}{2}}. \end{align*}$$
$$\begin{align*}\omega (f,t):= \sup_{| y| \leq t}\Big( \int_{ \mathbb{T}^{d}}| f(x+y)-f(x)| ^{2}dx\Big) ^{\frac{1}{2}}. \end{align*}$$
Also let
![]() $\alpha \geq 0$
. Then there exists a constant c independent of f such that
$\alpha \geq 0$
. Then there exists a constant c independent of f such that
 $$\begin{align*}\sum_{\xi \in \mathbb{Z}^{d}}\log ^{\alpha }( 1+| \xi|) | \widehat{f}(\xi)| ^{2}\leq c\sum_{j=0}^{+\infty }( 1+j^{\alpha }) \omega^{2}( f,2^{-j}). \end{align*}$$
$$\begin{align*}\sum_{\xi \in \mathbb{Z}^{d}}\log ^{\alpha }( 1+| \xi|) | \widehat{f}(\xi)| ^{2}\leq c\sum_{j=0}^{+\infty }( 1+j^{\alpha }) \omega^{2}( f,2^{-j}). \end{align*}$$
Proof One has
 $$ \begin{align*} \sum_{\xi \in \mathbb{Z}^{d}}\log ^{\alpha }(1+|\xi|) | \widehat{f}(\xi)|^{2} & \leq \sum_{j=0}^{+\infty }\log ^{\alpha }( 1+2^{j+1}) \sum_{2^{j}\leq |\xi\vert_{\infty} <2^{j+1}}| \widehat{f} (\xi)| ^{2}. \end{align*} $$
$$ \begin{align*} \sum_{\xi \in \mathbb{Z}^{d}}\log ^{\alpha }(1+|\xi|) | \widehat{f}(\xi)|^{2} & \leq \sum_{j=0}^{+\infty }\log ^{\alpha }( 1+2^{j+1}) \sum_{2^{j}\leq |\xi\vert_{\infty} <2^{j+1}}| \widehat{f} (\xi)| ^{2}. \end{align*} $$
It then suffices to show that
This inequality is well-known, but it is easier to give a proof than a reference. Parseval’s identity gives
 $$\begin{align*}\int_{\mathbb{T}^{d}}| f(x+y)-f(x)| ^{2}dx=\sum_{\xi \in \mathbb{Z}^{d}}| e^{2\pi i\xi y}-1| ^{2}| \widehat{f}(\xi)| ^{2}. \end{align*}$$
$$\begin{align*}\int_{\mathbb{T}^{d}}| f(x+y)-f(x)| ^{2}dx=\sum_{\xi \in \mathbb{Z}^{d}}| e^{2\pi i\xi y}-1| ^{2}| \widehat{f}(\xi)| ^{2}. \end{align*}$$
Write
![]() $\xi =(h,k) $
, with
$\xi =(h,k) $
, with
![]() $h\in \mathbb {Z}$
and
$h\in \mathbb {Z}$
and
![]() $k\in \mathbb {Z} ^{d-1}$
, and take
$k\in \mathbb {Z} ^{d-1}$
, and take
![]() $y= ( 2^{-j-2},0) $
. Then
$y= ( 2^{-j-2},0) $
. Then
![]() ${\xi y=2^{-j-2}h}$
, and
${\xi y=2^{-j-2}h}$
, and
 $$ \begin{align*} \sum_{\substack{(h,k) \in \mathbb{Z\times Z}^{d} \\ 2^{j}\leq |h| <2^{j+1} }}| \widehat{f}(\xi)| ^{2} & \leq c \sum_{\substack{(h,k) \in \mathbb{Z\times Z}^{d} \\ 2^{j}\leq |h|<2^{j+1} }}| e^{2\pi i2^{-j-2}h}-1| ^{2}| \widehat{f}(\xi)| ^{2} & \leq c \omega ^{2}( f,2^{-j-2}) &\leq c \omega ^{2}(f,2^{-j}). \end{align*} $$
$$ \begin{align*} \sum_{\substack{(h,k) \in \mathbb{Z\times Z}^{d} \\ 2^{j}\leq |h| <2^{j+1} }}| \widehat{f}(\xi)| ^{2} & \leq c \sum_{\substack{(h,k) \in \mathbb{Z\times Z}^{d} \\ 2^{j}\leq |h|<2^{j+1} }}| e^{2\pi i2^{-j-2}h}-1| ^{2}| \widehat{f}(\xi)| ^{2} & \leq c \omega ^{2}( f,2^{-j-2}) &\leq c \omega ^{2}(f,2^{-j}). \end{align*} $$
Iterating for each of the d coordinates of
![]() $\xi $
, one obtains
$\xi $
, one obtains
It is interesting to observe that, using the above proposition, Corollary 1.8 can be applied whenever f is the characteristic function of a domain with a fractal boundary with a minimally regular geometry. More precisely, let
![]() $\Omega \subseteq \mathbb T^d$
be a Borel measurable set, and suppose that there exists
$\Omega \subseteq \mathbb T^d$
be a Borel measurable set, and suppose that there exists
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
Notice that this is an assumption on the Minkowski content of
![]() $\partial \Omega $
. Then, for
$\partial \Omega $
. Then, for
![]() $0<\delta <\varepsilon $
,
$0<\delta <\varepsilon $
,
 $$ \begin{align*} \sum_{j=0}^{+\infty} (1+j^{1+\delta})\omega^2(\chi_\Omega,2^{-j}) & = \sum_{j=0}^{+\infty} (1+j^{1+\delta})\sup_{|y| \leq 2^{-j}} \int_{\mathbb T^d}|\chi_{\Omega}(x+y) - \chi_\Omega(x)|^2 dx \\ & \leq \sum_{j=0}^{+\infty} (1+j^{1+\delta}) |\{x\in \mathbb T^d: \operatorname{\mathrm{dist}}(x,\partial \Omega) \leq 2^{-j} \} | \\ & \leq c \Big(1+\sum_{j=1}^{+\infty}(1+j^{1+\delta})j^{-2-\varepsilon}\Big) < +\infty. \end{align*} $$
$$ \begin{align*} \sum_{j=0}^{+\infty} (1+j^{1+\delta})\omega^2(\chi_\Omega,2^{-j}) & = \sum_{j=0}^{+\infty} (1+j^{1+\delta})\sup_{|y| \leq 2^{-j}} \int_{\mathbb T^d}|\chi_{\Omega}(x+y) - \chi_\Omega(x)|^2 dx \\ & \leq \sum_{j=0}^{+\infty} (1+j^{1+\delta}) |\{x\in \mathbb T^d: \operatorname{\mathrm{dist}}(x,\partial \Omega) \leq 2^{-j} \} | \\ & \leq c \Big(1+\sum_{j=1}^{+\infty}(1+j^{1+\delta})j^{-2-\varepsilon}\Big) < +\infty. \end{align*} $$
Hence, by Proposition 4.1, we have that
Explicitly, from Corollary 1.8, we obtain that, for every matrix A satisfying (1.5), for every
![]() $\eta>0$
and for almost every
$\eta>0$
and for almost every
![]() $x\in \mathbb T^d$
, there exists
$x\in \mathbb T^d$
, there exists
![]() $C>0$
, depending on
$C>0$
, depending on
![]() $x, \eta , $
and A, such that for every
$x, \eta , $
and A, such that for every
![]() $N\in \mathbb N$
$N\in \mathbb N$
 $$ \begin{align} \Big|\frac{1}{N}\sum_{n=0}^{N-1} \chi_{\Omega}(A^n x) - |\Omega| \Big| \leq C N^{-\frac{1}{2} } \log N ^{\frac 32 + \eta}. \end{align} $$
$$ \begin{align} \Big|\frac{1}{N}\sum_{n=0}^{N-1} \chi_{\Omega}(A^n x) - |\Omega| \Big| \leq C N^{-\frac{1}{2} } \log N ^{\frac 32 + \eta}. \end{align} $$
It is interesting to compare the above estimate with some results in [Reference Brandolini, Colzani and TravagliniBCT23]. In particular, in [Reference Brandolini, Colzani and TravagliniBCT23, Corollary 4], it is proved that if
![]() $\Omega $
is such that for some
$\Omega $
is such that for some
![]() $\beta>0$
and for every
$\beta>0$
and for every
![]() $t>0$
, sufficiently small, one has
$t>0$
, sufficiently small, one has
and if
![]() $\Omega $
satisfies some other mild technical assumptions, then there exists a constant
$\Omega $
satisfies some other mild technical assumptions, then there exists a constant
![]() $c>0$
such that for every distribution of points
$c>0$
such that for every distribution of points
![]() $\{p_n\}_{n=0}^{N-1}$
there exists an affine copy
$\{p_n\}_{n=0}^{N-1}$
there exists an affine copy
![]() $\widetilde {\Omega }$
of
$\widetilde {\Omega }$
of
![]() $\Omega $
which satisfies the estimate
$\Omega $
which satisfies the estimate
 $$\begin{align*}\Big|\frac{1}{N}\sum_{n=0}^{N-1} \chi_{\widetilde{\Omega}}(p_n) - |\tilde{\Omega}| \Big|\geq cN^{-\frac{1}{2}-\frac{\beta}{2}}. \end{align*}$$
$$\begin{align*}\Big|\frac{1}{N}\sum_{n=0}^{N-1} \chi_{\widetilde{\Omega}}(p_n) - |\tilde{\Omega}| \Big|\geq cN^{-\frac{1}{2}-\frac{\beta}{2}}. \end{align*}$$
Moreover, in [Reference Brandolini, Colzani and TravagliniBCT23, Theorem 12], it is proved that, under the same hypothesis on
![]() $\Omega $
, there exists
$\Omega $
, there exists
![]() $c>0$
such that for every N there exists a distribution of N points
$c>0$
such that for every N there exists a distribution of N points
![]() $\{p_n\}_{n=1}^{N}$
such that
$\{p_n\}_{n=1}^{N}$
such that
 $$\begin{align*}\Big|\frac{1}{N}\sum_{n=0}^{N-1} \chi_{\widetilde{\Omega}}(p_n) - |\widetilde{\Omega}| \Big|\leq cN^{-\frac{1}{2}-\frac{\beta}{2}}, \end{align*}$$
$$\begin{align*}\Big|\frac{1}{N}\sum_{n=0}^{N-1} \chi_{\widetilde{\Omega}}(p_n) - |\widetilde{\Omega}| \Big|\leq cN^{-\frac{1}{2}-\frac{\beta}{2}}, \end{align*}$$
for “many” affine copies
![]() $\widetilde {\Omega }$
of
$\widetilde {\Omega }$
of
![]() $\Omega $
. We point out that in this last estimate the single set of points
$\Omega $
. We point out that in this last estimate the single set of points
![]() $\{p_n\}_{n=0}^{N-1}$
depends on
$\{p_n\}_{n=0}^{N-1}$
depends on
![]() $\Omega $
and N, while, in our estimate (4.1) the underlying sequence of points is fixed. However, notice that the numerology in our upper bound (4.1) tends to coincide, up to a logarithmic transgression, with the upper bound in [Reference Brandolini, Colzani and TravagliniBCT23, Theorem 12] when
$\Omega $
and N, while, in our estimate (4.1) the underlying sequence of points is fixed. However, notice that the numerology in our upper bound (4.1) tends to coincide, up to a logarithmic transgression, with the upper bound in [Reference Brandolini, Colzani and TravagliniBCT23, Theorem 12] when
![]() $\beta $
tends to
$\beta $
tends to
![]() $0$
.
$0$
.