Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sandling, Robert
1974.
Group rings of circle and unit groups.
Mathematische Zeitschrift,
Vol. 140,
Issue. 3,
p.
195.
Losey, Gerald
1974.
N-Series and Filtrations of the Augmentation Ideal.
Canadian Journal of Mathematics,
Vol. 26,
Issue. 4,
p.
962.
Tahara, Ken-ichi
1977.
The fourth dimension subgroups and polynomial maps.
Journal of Algebra,
Vol. 45,
Issue. 1,
p.
102.
TAHARA, Ken-ichi
1977.
On the structure of <i>Q</i><sub>3</sub> (<i>G</i>) and the fourth dimension subgroups.
Japanese journal of mathematics. New series,
Vol. 3,
Issue. 2,
p.
381.
Hales, A. W.
and
Passi, I. B. S.
1978.
The second augmentation quotient of an integral group ring.
Archiv der Mathematik,
Vol. 31,
Issue. 1,
p.
259.
Sandling, Robert
and
Tahara, Ken-Ichi
1979.
Augmentation quotients of group rings and symmetric powers.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 85,
Issue. 2,
p.
247.
Losey, Gerald
and
Losey, Nora
1979.
Augmentation quotients of some nonabelian finite groups.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 85,
Issue. 2,
p.
261.
Tahara, Ken-Ichi
1981.
The augmentation quotients of group rings and the fifth dimension subgroups.
Journal of Algebra,
Vol. 71,
Issue. 1,
p.
141.
Ritter, J�rgen
and
Sehgal, Sudarshan
1983.
Isomorphism of group rings.
Archiv der Mathematik,
Vol. 40,
Issue. 1,
p.
32.
Khambadkone, Meera
1983.
Subgroup ideals in grouprings I.
Journal of Pure and Applied Algebra,
Vol. 30,
Issue. 3,
p.
261.
Khambadkone, Meera
1985.
Augmentation quotients of semidirect products.
Archiv der Mathematik,
Vol. 45,
Issue. 5,
p.
407.
Khambadkone, Meera
1985.
On the structure of augmentation ideals in group rings.
Journal of Pure and Applied Algebra,
Vol. 35,
Issue. ,
p.
35.
Khambadkone, Meera
1986.
Subgroup ideals in group rings III.
Communications in Algebra,
Vol. 14,
Issue. 3,
p.
411.
Hartl, Manfred
1995.
Some successive quotients of group ring filtrations induced by n-series.
Communications in Algebra,
Vol. 23,
Issue. 10,
p.
3831.
Sehgal, S.K.
2003.
Vol. 3,
Issue. ,
p.
455.
Gumber, Deepak Kumar
Karan, Ram
and
Pal, Indu
2008.
Some augmentation quotients of integral group rings.
Proceedings Mathematical Sciences,
Vol. 118,
Issue. 4,
p.
537.
Hartl, Manfred
2010.
On Fox and augmentation quotients of semidirect products.
Journal of Algebra,
Vol. 324,
Issue. 12,
p.
3276.


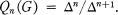 . It is well-known that
. It is well-known that 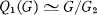 (see, for example [
(see, for example [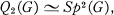 , the second symmetric power of
, the second symmetric power of 