Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T14:53:48.815Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Tempered Spectrum of Quasi-Split Classical Groups II

Published online by Cambridge University Press:  20 November 2018

David Goldberg  and
Freydoon Shahidi
David Goldberg
Affiliation:
Department of Mathematics Purdue University West Lafayette, Indiana 47907 U.S.A.
Freydoon Shahidi
Affiliation:
Department of Mathematics Purdue University West Lafayette, Indiana 47907 U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We determine the poles of the standard intertwining operators for a maximal parabolic subgroup of the quasi-split unitary group defined by a quadratic extension 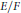$E/F$ of 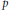$p$-adic fields of characteristic zero. We study the case where the Levi component 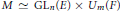$M\simeq \text{G}{{\text{L}}_{n}}\left( E \right)\times {{U}_{m}}\left( F \right)$, with 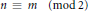$n\,\equiv \,m\,\left( \bmod \,2 \right)$. This, along with earlier work, determines the poles of the local Rankin-Selberg product $L$-function 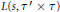$L\left( s,\,{\tau }'\,\times \,\tau \right)$, with 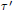${\tau }'$ an irreducible unitary supercuspidal representation of 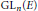$\text{G}{{\text{L}}_{n}}\left( E \right)$ and $\tau $ a generic irreducible unitary supercuspidal representation of 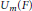${{U}_{m}}\left( F \right)$. The results are interpreted using the theory of twisted endoscopy.

Keywords

22E5011S70
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 53 , Issue 2 , 01 April 2001 , pp. 244 - 277
Copyright
Copyright © Canadian Mathematical Society 2001

References

[1] Arthur, J., The local behaviour of weighted orbital integrals. Duke Math. J. 56 (1988), 223–293.Google Scholar
[2] Arthur, J., Unipotent automorphic representations: conjectures. Astérisque 171-172 (1989), 13–71.Google Scholar
[3] Arthur, J., Unipotent automorphic representations: Global motivations. In: Automorphic Forms, Shimura Varieties, and L–functions, Vol I, (eds. L. Clozel and J. S. Milne), Academic Press, New York, New York, Perspectives in Mathemetics 10, 1990, 1–75.Google Scholar
[4] Clozel, L., Characters of non-connected reductive p-adic groups. Canad. J. Math. (1) 39 (1987), 149–167.Google Scholar
[5] Clozel, L., Invariant harmonic analysis on the Schwartz space of a reductive p-adic group. In: Harmonic Analysis on Reductive Groups, (eds.W. Barker and P. Sally), Birkhäuser Boston, Cambridge, MA, 1991, 101–121.Google Scholar
[6] Goldberg, D., Reducibility of generalized principal series representations for U(2, 2) via base change. Compositio Math. 85 (1993), 245–264.Google Scholar
[7] Goldberg, D., Some results on reducibility for unitary groups and local Asai L-functions. J. Reine Angew Math. 448 (1994), 65–95.Google Scholar
[8] Goldberg, D. and Shahidi, F., On the tempered spectrum of quasi-split classical groups. Duke Math. J. 92, 255–294.Google Scholar
[9] Harish-Chandra, , Harmonic Analysis on Reductive p-adic Groups. Springer-Verlag, Notes by G. van Dijk 162, New York, Heidelberg, Berlin, 1970.Google Scholar
[10] Harish-Chandra, , Harmonic analysis on reductive p-adic groups. Proc. Sympos. Pure Math. 26, Amer. Math. Soc., Providence, Rhode Island, 1973, 167–192.Google Scholar
[11] Kazhdan, D., Cuspidal geometry of p-adic groups. J. Analyse Math. 47 (1986), 1–36.Google Scholar
[12] Kottwitz, R. and Shelstad, D., Foundations of Twisted Endoscopy. Astérisque 255(1999).Google Scholar
[13] Shahidi, F., Poles of intertwining operators via endoscopy; the connection with prehomogeneous vector spaces, with an appendix: Basic endoscopic data by D. Shelstad, Dedicated to the memory of Magdy Assem. Compositio Math. 120 (2000), 291–325.Google Scholar
[14] Shahidi, F., A proof of Langlands conjecture for Plancherel measures; complementary series for p-adic groups. Ann. of Math. (2) 132 (1990), 273–330.Google Scholar
[15] Shahidi, F., Twisted endoscopy and reducibility of induced representations for p-adic groups. Duke Math. J. 66 (1992), 1–41.Google Scholar
[16] Shahidi, F., The notion of norm and the representation theory of orthogonal groups. Invent.Math. 119 (1995), 1–36.Google Scholar
[17] Shokranian, S., Geometric expansion of the local twisted trace formula. preprint.Google Scholar
[18] Springer, T. A., The classification of involutions of simple algebraic groups. J. Fac. Sci. Univ. Tokyo Sect. IA Math. 34 (1987), 655–670.Google Scholar