Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-15T05:40:00.015Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Unitary Equivalence of Certain Classes of Non-Normal Operators. I

Published online by Cambridge University Press:  20 November 2018

P. K. Tam
P. K. Tam*
Affiliation:
New Asia College, Kowloon, Hong Kong
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The following (so-called unitary equivalence) problem is of paramount importance in the theory of operators: given two (bounded linear) operators A1, A2 on a (complex) Hilbert space 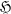, determine whether or not they are unitarily equivalent, i.e., whether or not there is a unitary operator U on 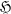such that U*A1U = A2. For normal operators this question is completely answered by the classical multiplicity theory [7; 11]. Many authors, in particular, Brown [3], Pearcy [9], Deckard [5], Radjavi [10], and Arveson [1; 2], considered the problem for non-normal operators and have obtained various significant results. However, most of their results (cf. [13]) deal only with operators which are of type I in the following sense [12]: an operator, A, is of type I (respectively, II1, II∞, III) if the von Neumann algebra generated by A is of type I (respectively, II1, II∞, III).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 23 , Issue 5 , October 1971 , pp. 849 - 856
Copyright
Copyright © Canadian Mathematical Society 1971

Footnotes

The results of this paper constitute part of the author's doctoral dissertation, written at the University of British Columbia under the supervision of Dr. Donald J. Bures.

References

1. Arveson, W. B., Subalgebras of C*-algebras, Acta Math. 123 (1969), 142–224.Google Scholar
2. Arveson, W. B., Unitary invariants for compact operators, Bull. Amer. Math. Soc. 76 (1970), 88–91.Google Scholar
3. Brown, A., The unitary equivalence ofbinormal operators, Amer. J. Math. 76 (1954), 414–434.Google Scholar
4. Bures, D., Abelian subalgebras of von Neumann algebras, preprint (to be published in the Memoirs of Amer. Math. Soc.).Google Scholar
5. Deckard, D., Complete sets of unitary invariants for compact and trace-class operators, Acta Sci. Math. (Szeged) 28 (1967), 9–20.Google Scholar
6. Dixmier, J., Les algebres à'opérateurs dans l'espace Hilbertien, second edition (Gauthier- Villars, Paris, 1969).Google Scholar
7. Halmos, P. R., Introduction to Hilbert space and the theory of spectral multiplicity (Chelsea, New York, 1951).Google Scholar
8. Neumann, J. von and Murray, F. J., On rings of operators. III, Ann of Math. 1^1 (1940), 94–161.Google Scholar
9. Pearcy, C., A complete set of unitary invariants for operators generating finite W*-algebras of type I, Pacific J. Math. 12 (1962), 1405–1416.Google Scholar
10. Radjavi, H., Simultaneous unitary invariants for sets of bounded operators on a Hilbert space, Ph.D. Thesis, University of Minnesota, 1962.Google Scholar
11. Segal, I. E., Decompositions of operator algebras. II, Memoirs of Amer. Math. Soc, No. 9 (Amer. Math. Soc. Providence, R.I., 1951).Google Scholar
12. Suzuki, N., Isometries on Hilbert spaces, Proc. Japan Acad. 39 (1963), 435–438.Google Scholar
13. Suzuki, N., Algebraic aspects of non self-adjoint operators, Proc. Japan Acad. I±l (1965), 706–710.Google Scholar
14. Tarn, P. K., On the commutant of certain automorphism groups, pre-print.Google Scholar