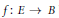Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
ARIMA, Ken-ichiro
and
SHIMADA, Ichiro
2009.
Zariski-van Kampen Method and Transcendental Lattices of Certain Singular $K3$ Surfaces.
Tokyo Journal of Mathematics,
Vol. 32,
Issue. 1,
SHIMADA, ICHIRO
2010.
GENERALIZED ZARISKI–VAN KAMPEN THEOREM AND ITS APPLICATION TO GRASSMANNIAN DUAL VARIETIES.
International Journal of Mathematics,
Vol. 21,
Issue. 05,
p.
591.
Ishige, Toshimasa
and
Takayasu, Akitoshi
2026.
Computer-assisted proofs for finding the monodromy of Picard–Fuchs differential equations for a family of K3 toric hypersurfaces.
Communications in Nonlinear Science and Numerical Simulation,
Vol. 152,
Issue. ,
p.
109408.