Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T14:26:52.039Z Has data issue: false hasContentIssue false
  • English
  • Français

One-dimensional Schubert Problems with Respect to Osculating Flags

Published online by Cambridge University Press:  20 November 2018

Jake Levinson
Jake Levinson*
Affiliation:
Mathematics Department, University of Michigan, Ann Arbor, MI e-mail: jakelev@umich.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider Schubert problems with respect to flags osculating the rational normal curve. These problems are of special interest when the osculation points are all real. In this case, for zero-dimensional Schubert problems, the solutions are “ as real as possible”. Recent work by Speyer has extended the theory to the moduli space 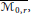$\overline{{{\mathcal{M}}_{0,\,r}}}$ allowing the points to collide. This gives rise to smooth covers 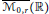$\overline{{{\mathcal{M}}_{0,\,r}}}\left( \mathbb{R} \right)$, with structure and monodromy described by Young tableaux and jeu de taquin.

In this paper, we give analogous results on one-dimensional Schubert problems over 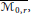$\overline{{{\mathcal{M}}_{0,\,r}}}$.Their(real) geometry turns out to be described by orbits of Schützenberger promotion and a related operation involving tableau evacuation. Over 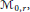${{\mathcal{M}}_{0,\,r}}$, our results show that the real points of the solution curves are smooth.

We also find a new identity involving “first-order” $\text{K}$-theoretic Littlewood-Richardson coefficients, for which there does not appear to be a known combinatorial proof.

Keywords

14N1505E99Schubert calculusstable curvesShapiro-Shapiro Conjecturejeu de taquingrowth diagrampromotion
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 69 , Issue 1 , 01 February 2017 , pp. 143 - 185
Copyright
Copyright © Canadian Mathematical Society 2017

References

[BSS96] Benkart, G., Sottile, F., and Stroomer, J., Tableau switching: Algorithms and applications. J. Combin. Theory Ser. A 76(1996), no. 1,11–43. http://dx.doi.Org/10.1006/jcta.1996.0086 Google Scholar
[BucO2] Buch, A. S., A Littlewood-Richardson rule for the K-theory of Grassmannians. Acta Math. 189(2002), no. 1, 37–78. http://dx.doi.org/10.1007/BF02392644 Google Scholar
[DevO4] Devadoss, S. L., Combinatorial equivalence of real moduli spaces. Notices Amer. Math. Soc. 51(2004), 620–628.Google Scholar
[EH86] Eisenbud, D. and Harris, J., Limit linear series: basic theory. Invent. Math. 85(1986), no. 2, 337–371. http://dx.doi.Org/10.1007/BF01389094 Google Scholar
[GH78] Griffiths, P. and Harris, J., Principles of algebraic geometry. Pure and Applied Mathematics, Wiley-Interscience[John Wiley & Sons], New York, 1978.Google Scholar
[GH81] Gross, B.H and Harris, J., Real algebraic curves. Ann. Sci. Éc. Norm. Sup. 14 (1981), no. 2,157–182.Google Scholar
[Hai92] Haiman, M. D., Dual equivalence with applications, including a conjecture of Proctor. Discrete Math. 99(1992), no. 1-3, 79–113. http://dx.doi.org/10.1016/0012-365X(92)90368-P Google Scholar
[Mat86] Matsumura, H.,Commutative ring theory. Cambridge Studies in Advanced Mathematics, 8, Cambridge University Press, Cambridge, 1986.Google Scholar
[MTV09] Mukhin, E., Tarasov, V., and Varchenko, A.,Schubert calculus and representations of the general linear group. J. Amer. Math. Soc. 22(2009), no. 4, 909–940. http://dx.doi.Org/10.1090/S0894-0347-09-00640-7 Google Scholar
[PurlO] Purbhoo, K., Jeu de taquin and a monodromy problem for Wronskians of polynomials. Adv. Math. 224(2010), no. 3, 827–862. http://dx.doi.Org/10.1016/j.aim.2009.12.013 Google Scholar
[SotlO] Sottile, E.,Frontiers of reality in Schubert calculus. Bull. Amer. Math. Soc. 47(2010), no. 1, 31–71. http://dx.doi.org/10.1090/S0273-0979-09-01276-2 Google Scholar
[Spel4] Speyer, D. E., Schubert problems with respect to osculating flags of stable rational curves. Algebr. Geom. 1(2014), no. 1, 14–45. http://dx.doi.org/10.14231/AC-2014-002 Google Scholar
[StaOl] Stanley, R., Enumerative combinatorics, vol. 2, Cambridge Studies in Advanced Mathematics, Cambridge University Press, Cambridge, 2001.Google Scholar
[TY09] Thomas, H. and Yong, A., A jeu de taquin theory for increasing tableaux, with applications to K-theoretic Schubert calculus. Algebra Number Theory 3(2009), no. 2,121–148.http://dx.doi.org/10.2140/ant.2009.3.121 Google Scholar