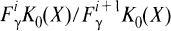Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Nicas, Andrew J.
1987.
Mixed Hodge structure in cyclic homology and algebraic K-theory, 1.
K-Theory,
Vol. 1,
Issue. 5,
p.
437.
Gillet, H.
and
Soul�, C.
1987.
Intersection theory using Adams operations.
Inventiones Mathematicae,
Vol. 90,
Issue. 2,
p.
243.
Deninger, Christopher
and
Wingberg, Kay
1988.
Beilinson's Conjectures on Special Values of L-Functions.
p.
249.
Schneider, Peter
1988.
Beilinson's Conjectures on Special Values of L-Functions.
p.
1.
Snaith, Victor
1988.
Explicit Brauer induction.
Inventiones Mathematicae,
Vol. 94,
Issue. 3,
p.
455.
TAMME, GÜNTER
1988.
Beilinson's Conjectures on Special Values of L-Functions.
p.
103.
Neukirch, Jürgen
1988.
Beilinson's Conjectures on Special Values of L-Functions.
p.
193.
Deninger, Christopher
1989.
Higher regulators and HeckeL-series of imaginary quadratic fields I.
Inventiones Mathematicae,
Vol. 96,
Issue. 1,
p.
1.
Sah, Chin-Han
1989.
Homology of classical lie groups made discrete, III.
Journal of Pure and Applied Algebra,
Vol. 56,
Issue. 3,
p.
269.
Cathelineau, Jean-Louis
1990.
λ-structures in algebraic K-theory and cyclic homology.
K-Theory,
Vol. 4,
Issue. 6,
p.
591.
Franke, J.
1990.
Algebraic Geometry.
p.
101.
Lichtenbaum, S.
1990.
The Grothendieck Festschrift Volume III.
Vol. 88,
Issue. ,
p.
35.
Gillet, Henri
and
Soulé, Christophe
1990.
Arithmetic intersection theory.
Publications mathématiques de l'IHÉS,
Vol. 72,
Issue. 1,
p.
94.
Gerdes, Wolfram
1991.
The linearization of higher Chow cycles of dimension one.
Duke Mathematical Journal,
Vol. 62,
Issue. 1,
Weibel, Charles A.
1991.
Pic is a contracted functor.
Inventiones Mathematicae,
Vol. 103,
Issue. 1,
p.
351.
Berhard, Köck
1991.
The Lefschetz Theorem in Higher EquivariantK-theory.
Communications in Algebra,
Vol. 19,
Issue. 12,
p.
3411.
Arlettaz, Dominique
1991.
The Hurewicz homomorphism in algebraic K-theory.
Journal of Pure and Applied Algebra,
Vol. 71,
Issue. 1,
p.
1.
Hanlon, Phil
1992.
Order and disorder in algebraic combinatorics.
The Mathematical Intelligencer,
Vol. 14,
Issue. 2,
p.
20.
Levine, Marc
1992.
Relative MilnorK-theory.
K-Theory,
Vol. 6,
Issue. 2,
p.
113.
Gillet, Henri
1992.
Higher Algebraic K-Theory: an overview.
Vol. 1491,
Issue. ,
p.
55.
 -modules localement libres sur un schéma X[14]. La somme directe et le produit tensoriel de modules font de K0(X) un anneau, et les opérations de puissances extérieures lui fournissent une structure supplémentaire, que Grothendieck appelle λ-anneau. Un λ-anneau est muni d'une filtration décroissante, la γ-filtration, et un des principaux résultats de Grothendieck est que, si X est lisse sur un corps, le groupe
-modules localement libres sur un schéma X[14]. La somme directe et le produit tensoriel de modules font de K0(X) un anneau, et les opérations de puissances extérieures lui fournissent une structure supplémentaire, que Grothendieck appelle λ-anneau. Un λ-anneau est muni d'une filtration décroissante, la γ-filtration, et un des principaux résultats de Grothendieck est que, si X est lisse sur un corps, le groupe