Article contents
Operators of the form PAQ-QAP
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In this note the Hilbert spaces under consideration are complex, and the operators referred to are bounded, linear operators. If 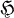 is a Hilbert space, then the algebra of all operators on
is a Hilbert space, then the algebra of all operators on 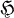 is denoted by
is denoted by 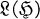 .
.
It is known (1) that if 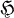 is any Hilbert space, then the class of commutators on
is any Hilbert space, then the class of commutators on 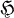 , i.e., the class of all operators that can be written in the form PQ — QP for some
, i.e., the class of all operators that can be written in the form PQ — QP for some 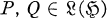 , can be exactly described. A similar problem is that of characterizing all operators on
, can be exactly described. A similar problem is that of characterizing all operators on 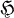 that can be written in the form
that can be written in the form 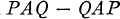 for some
for some 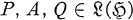 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1968
Footnotes
This research was supported in part by the National Science Foundation. At the time the paper was written, the second author was an Alfred P. Sloan Research Fellow.
References
1.
Brown, A. and Pearcy, C., Structure of commutators of operators, Ann. of Math. (2) 82 (1965), 112–127.Google Scholar
2.
Brown, A., Halmos, P. R., and Pearcy, C., Commutators of operators on Hilbert space, Can. J. Math. 17 (1965), 695–708.Google Scholar
3.
Lumer, G. and Rosenblum, M., Linear operator equations, Proc. Amer. Math. Soc. 10 (1959), 32–41.Google Scholar
4.
Taussky, O., Generalized commutators of matrices and permutations of factors in a product of three matrices (Studies in Mathematics and Mechanics presented to Richard von Mises, Academic Press, New York, 1954).Google Scholar
- 4
- Cited by

