Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Brown, L. G.
Douglas, R. G.
and
Fillmore, P. A.
1973.
Extensions of 𝐶*-algebras, operators with compact self-commutators, and 𝐾-homology.
Bulletin of the American Mathematical Society,
Vol. 79,
Issue. 5,
p.
973.
Fialkow, L. A.
1975.
The similarity orbit of a normal operator.
Transactions of the American Mathematical Society,
Vol. 210,
Issue. 0,
p.
129.
Pearcy, Carl
and
Salinas, Norberto
1977.
K-Theory and Operator Algebras.
Vol. 575,
Issue. ,
p.
96.

 be a fixed separable, infinite dimensional complex Hilbert space, and let
be a fixed separable, infinite dimensional complex Hilbert space, and let 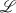 (
(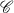 and the canonical quotient map from
and the canonical quotient map from 