Article contents
Optimal Quotients of Jacobians With ToricReduction and Component Groups
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 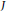 $J$ be a Jacobian variety with toric reduction over a local field
$J$ be a Jacobian variety with toric reduction over a local field  $K$. Let
$K$. Let 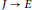 $J\,\to \,E$ be an optimal quotient defined over
$J\,\to \,E$ be an optimal quotient defined over  $K$, where
$K$, where  $E$ is an elliptic curve. We give examples in which the functorially induced map
$E$ is an elliptic curve. We give examples in which the functorially induced map 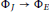 ${{\Phi }_{J}}\,\to \,{{\Phi }_{E}}$ on component groups of the Néron models is not surjective. This answers a question of Ribet and Takahashi. We also give various criteria under which
${{\Phi }_{J}}\,\to \,{{\Phi }_{E}}$ on component groups of the Néron models is not surjective. This answers a question of Ribet and Takahashi. We also give various criteria under which 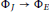 ${{\Phi }_{J}}\,\to \,{{\Phi }_{E}}$ is surjective and discuss when these criteria hold for the Jacobians of modular curves.
${{\Phi }_{J}}\,\to \,{{\Phi }_{E}}$ is surjective and discuss when these criteria hold for the Jacobians of modular curves.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2016
References
- 1
- Cited by


