Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-11T01:54:52.205Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal Roughening of Convex Bodies

Published online by Cambridge University Press:  20 November 2018

Alexander Plakhov
Alexander Plakhov*
Affiliation:
University of Aveiro, Department of Mathematics, Aveiro 3810-193, Portugal email: plakhov@ua.pt Institute for Information Transmission Problems, Moscow 127994, Russia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A body moves in a rarefied medium composed of point particles at rest. The particles make elastic reflections when colliding with the body surface and do not interact with each other. 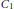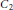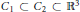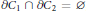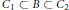We consider a generalization of Newton’s minimal resistance problem: given two bounded convex bodies ${{C}_{1}}$ and ${{C}_{2}}$ such that ${{C}_{1}}\,\subset \,{{C}_{2}}\,\subset \,{{\mathbb{R}}^{3}}$ and $\partial {{C}_{1}}\,\cap \,\partial {{C}_{2}}\,=\,\varnothing $, minimize the resistance in the class of connected bodies $B$ such that ${{C}_{1}}\,\subset \,B\,\subset \,{{C}_{2}}$. We prove that the infimum of resistance is zero; that is, there exist “almost perfectly streamlined” bodies.

Keywords

37D5049Q10billiardsshape optimizationproblems of minimal resistanceNewtonian aerodynamicsrough surface
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 5 , 01 October 2012 , pp. 1058 - 1074
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Belloni, M. and Kawohl, B., A paper of Legendre revisited. Forum Math. 9(1997), 655–667. http://dx.doi.org/10.1515/form.1997.9.655 Google Scholar
[2] Belloni, M. and A.Wagner, Newton's problem of minimal resistance in the class of bodies with prescribed volume. J. Convex Anal. 10(2003), 491–500.Google Scholar
[3] Brock, F., Ferone, V., and Kawohl, B., A symmetry problem in the calculus of variations. Calc. Var. Partial Differential Equations 4(1996), no. 6, 593–599. http://dx.doi.org/10.1007/BF01261764 Google Scholar
[4] Bucur, D. and Buttazzo, G., Variational methods in shape optimization problems. Progress in Nonlinear Differential Equations and their Applications, 65, Birkhäuser Boston, Boston, MA, 2005.Google Scholar
[5] Buttazzo, G., Ferone, V., and Kawohl, B., Minimum problems over sets of concave functions and related questions. Math. Nachr. 173(1995), 71–89. http://dx.doi.org/10.1002/mana.19951730106 Google Scholar
[6] Buttazzo, G. and Guasoni, P., Shape optimization problems over classes of convex domains. J. Convex Anal. 4(1997), no. 2, 343–351.Google Scholar
[7] Buttazzo, G. and Kawohl, B., On Newton's problem of minimal resistance. Math. Intelligencer 15(1993), no. 4, 7–12. http://dx.doi.org/10.1007/BF03024318 Google Scholar
[8] Comte, M. and Lachand-Robert, T., Newton's problem of the body of minimal resistance under a single-impact assumption. Calc. Var. Partial Differential Equations 12(2001), no. 2, 173–211. http://dx.doi.org/10.1007/PL00009911 Google Scholar
[9] Comte, M. and Lachand-Robert, T., Existence of minimizers for Newton's problem of the body of minimal resistance under a single impact assumption. J. Anal. Math. 83(2001), 313–335. http://dx.doi.org/10.1007/BF02790266 Google Scholar
[10] Comte, M. and Lachand-Robert, T., Functions and domains having minimal resistance under a single-impact assumption. SIAM J. Math. Anal. 34(2002), no. 1, 101–120. http://dx.doi.org/10.1137/S0036141001388841 Google Scholar
[11] Lachand-Robert, T. and Peletier, M. A., Newton's problem of the body of minimal resistance in the class of convex developable functions. Math. Nachr. 226(2001), 153–176. http://dx.doi.org/10.1002/1522-2616(200106)226:1h153::AID-MANA153i3.0.CO;2-2 Google Scholar
[12] Lachand-Robert, T. and Peletier, M. A., An example of non-convex minimization and an application to Newton's problem of the body of least resistance. Ann. Inst. H. Poincaré, Anal. Non Linéaire 18(2001), no. 2, 179–198. http://dx.doi.org/10.1016/S0294-1449(00)00062-7 Google Scholar
[13] Newton, I., Philosophiae Naturalis Principia Mathematica. Streater, London, 1687.Google Scholar
[14] Plakhov, A., Billiard scattering on rough sets: two-dimensional case. SIAM J. Math. Anal. 40(2009), no. 6, 2155–2178. http://dx.doi.org/10.1137/070709700 Google Scholar
[15] Plakhov, A., Billiards and two-dimensional problems of optimal resistance. Arch. Ration. Mech. Anal. 194(2009), no. 2, 349–381. http://dx.doi.org/10.1007/s00205-008-0137-1 Google Scholar
[16] Plakhov, A., Scattering in billiards and problems of Newtonian aerodynamics. (Russian) Uspekhi Mat. Nauk. 64(2009), no. 5(389), 97–166; English translation in Russ. Math. Surv. 64(2009), no. 5, 873–938.Google Scholar