Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Essén, Matts
1987.
General Inequalities 5.
p.
347.
Holmåker, Kjell
1989.
An optimization problem for the differential equation y″ − qy = 0.
Journal of Mathematical Analysis and Applications,
Vol. 144,
Issue. 2,
p.
377.
Holmåker, Kjell
1992.
An optimization problem for a second order differential equation with oscillating solutions.
Journal of Mathematical Analysis and Applications,
Vol. 169,
Issue. 2,
p.
420.
Kovalev, Leonid V.
2005.
Comparison theorems for the one-dimensional Schrödinger equation.
Arkiv för Matematik,
Vol. 43,
Issue. 2,
p.
403.


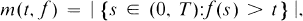
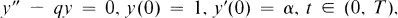
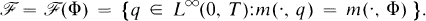
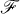 or in the convex hull Ω(Φ) of
or in the convex hull Ω(Φ) of 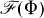 (see below).
(see below).