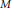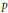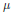Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Heiermann, V.
and
Muić, G.
2007.
On the standard modules conjecture.
Mathematische Zeitschrift,
Vol. 255,
Issue. 4,
p.
847.
Heiermann, Volker
2016.
A note on standard modules and Vogan L-packets.
Manuscripta Mathematica,
Vol. 150,
Issue. 3-4,
p.
571.
Heiermann, Volker
and
Kim, Yeansu
2016.
On the generic local Langlands correspondence for 𝐺𝑆𝑝𝑖𝑛 groups.
Transactions of the American Mathematical Society,
Vol. 369,
Issue. 6,
p.
4275.
Heiermann, Volker
2017.
Local Langlands correspondence for classical groups and affine Hecke algebras.
Mathematische Zeitschrift,
Vol. 287,
Issue. 3-4,
p.
1029.
Moussaoui, Ahmed
2017.
Centre de Bernstein dual pour les groupes classiques.
Representation Theory of the American Mathematical Society,
Vol. 21,
Issue. 10,
p.
172.
Silberger, Allan J.
and
Zink, Ernst-Wilhelm
2018.
Langlands classification for L-parameters.
Journal of Algebra,
Vol. 511,
Issue. ,
p.
299.
Imai, Naoki
2024.
Local Langlands correspondences in $$\ell $$-adic coefficients.
manuscripta mathematica,
Vol. 175,
Issue. 1-2,
p.
345.