Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T00:46:33.871Z Has data issue: false hasContentIssue false
  • English
  • Français

Ordering Uniform Completions of Partially Ordered Sets

Published online by Cambridge University Press:  20 November 2018

R. H. Redfield
R. H. Redfield*
Affiliation:
Simon Fraser University, Burnaby, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

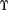Let (P, ) be a (nearly) uniform ordered space. Let (P, 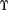) be the uniform completion of (P, 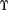) at 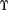. Several partial orders for P are introduced and discussed. One of these orders provides an adjoint to the functor which embeds the category of uniformly complete uniform ordered spaces in the category of uniform ordered spaces, both categories with uniformly continuous order-preserving functions. When P is a join-semilattice with uniformly continuous join, two of these orders coalesce to the unique partial order with respect to which P is a join-semilattice, P is a join-subsemilattice of P, and the join on P is continuous.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 3 , June 1974 , pp. 644 - 664
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Birkhoff, G., Lattice theory, 3rd. edition (Amer. Math. Soc. Colloquium Pub. 25, Providence, 1967).Google Scholar
2. Birkhoff, G. and MacLane, S., Algebra (MacMillan Co., New York, 1967).Google Scholar
3. Bourbaki, N., General topology (Addison-Wesley Pub. Co., Don Mills, Ontario, 1966). (translated from the French, Hermann, Paris.)Google Scholar
4. Conrad, P., The topological completion and the linearly compact hull of an abelian l-group (to appear).Google Scholar
5. Kiseleva, T. G., Partially ordered sets endowed with a uniform structure (Russian), Vestnik Leningrad. Univ. 22 (1967), no. 13, 51–57.Google Scholar
6. Nachbin, L., Topology and order (D. Van Nostrand Company, Inc., Princeton, 1965).Google Scholar
7. Thron, W., Topological structures (Holt, Rinehart and Winston, New York, 1966).Google Scholar