Article contents
Ordinary Singularities with Decreasing Hilbert Function
Published online by Cambridge University Press: 20 November 2018
Extract
Let A be the co-ordinate ring of a reduced curve over a field k. This means that A is an algebra of finite type over k, A has no nilpotent elements, and that if P is a minimal prime ideal of A, then A/P is an integral domain of Krull dimension one. Let M be a maximal ideal of A. Then G(A) (the graded ring of A relative to M) is defined to be 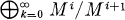 . We get the same graded ring if we first localize at M, and then form the graded ring of AM relative to the maximal ideal MAM. That is
. We get the same graded ring if we first localize at M, and then form the graded ring of AM relative to the maximal ideal MAM. That is
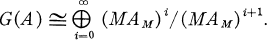
Let Ā be the integral closure of A. If P1, P2, …, Ps are the minimal primes of A then
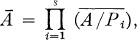
where A/Pi is a domain and 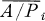 is the integral closure of A/Pi in its quotient field.
is the integral closure of A/Pi in its quotient field.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1982
References
- 4
- Cited by


