Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T06:23:44.399Z Has data issue: false hasContentIssue false
  • English
  • Français

Orthogonality of Certain Functions with Respect to Complex Valued Weights

Published online by Cambridge University Press:  20 November 2018

George Gasper
George Gasper*
Affiliation:
Northwestern University, Evanston, Illinois
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In his work on the Dirichlet problem for the Heisenberg group Greiner [5] showed that each Lα-spherical harmonic is a unique linear combination of functions of the form

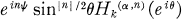
with k = 0, 1,2, … and n = 0, ±l, ±2 , …, where Hk(α, n)(θiθ) is defined by the generating function

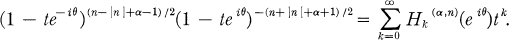
Since Hk(0,0)(eiθ) = Pk(cos θ), where Pk(x) is the Legendre polynomial of degree k, and these functions satisfy the orthogonality relation

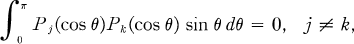
Greiner raised the question of whether the functions Hk(0,0)(eiθ) are orthogonal or biorthogonal with respect to some complex valued weight function.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 5 , 01 October 1981 , pp. 1261 - 1270
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Askey, R. and Ismail, M. E.-H., A generalization of ultraspherical polynomials, Studies in Pure Math., to appear.Google Scholar
2. Freund, G., Orthogonal polynomials, (Pergamon Press, New York, 1971).Google Scholar
3. Gasper, G., Summation formulas for basic hyper geometric series, SIAM J. Math. Anal. 12 (1981), 196–200.Google Scholar
4. Geronimus, Ya. L., Polynomials orthogonal on a circle and interval, (Pergamon Press, New York, 1960).Google Scholar
5. Greiner, P. C., Spherical harmonics on the Heisenberg group, Canadian Math. Bull. 28 (1980), 383–396.Google Scholar
6. Jones, W. B. and Thron, W. J., Orthogonal Laurent polynomials and Gaussian quadrature, to appear.Google Scholar
7. Karlsson, Per W., Hyper geometric functions with integral parameter differences, J. Math. Physics 12 (1971), 270–271.Google Scholar
8. Minton, B. M., Generalized hyper geometric functions of unit argument, J. Math. Physics 11 (1970), 1375–1376.Google Scholar
9. Muckenhoupt, B. and Stein, E. M., Classical expansions and their relation to conjugate harmonic functions, Trans. Amer. Math. Soc. 118 (1965), 17–92.Google Scholar
10. Slater, L. J., Generalized hyper geometric functions, (Cambridge Univ. Press, Cambridge, 1966).Google Scholar
11. Szego, G., Orthogonal polynomials, Amer. Math. Soc. Coll. Publ. 23, Fourth Edition (Providence, R.I., 1975).Google Scholar