Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-16T01:32:20.669Z Has data issue: false hasContentIssue false
  • English
  • Français

P and D in P-1XP = dg(λ, … , λn) = D As Matrix Functions of X

Published online by Cambridge University Press:  20 November 2018

R. F. Rinehart
R. F. Rinehart*
Affiliation:
U.S. Naval Postgraduate School, Monterey, California
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 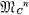be the algebra of n X n matrices over the complex field C, X = ‖xrs‖ a matrix of 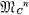, and f(X) = ‖(frs(x11, x12, … , xnn)‖ a function with domain and range in 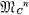. If the frs are differentiable with respect to each of the xij on some open set R of 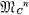, then the differential df(X) = ‖dfrs(xij)‖ exists, and, moreover, f(X) is Hausdorff-differentiable (HD) (1, 3, 7) i.e. df(X)is expressible in the form

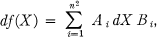
where dX = ‖dxrs‖, and the matrices Ai Bi are independent of dX. The Hausdorff derivative fI(X) is defined to be

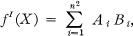
i.e. the value of df(X) for dX = I, the identity matrix (2).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 18 , 1966 , pp. 832 - 837
Copyright
Copyright © Canadian Mathematical Society 1966

References

1. Hausdorff, F., Zur Theorie der Systeme complexer Zahlen, Ber. Sachs. Akad. Wiss. Leipzig, 52 (1900), 43–61.Google Scholar
2. Portmann, W. O., A derivative for Hausdorff-analytic functions, Proc. Amer. Math. Soc., 10 (1959), 101–105.Google Scholar
3. Portmann, W. O., Hausdorff-analytic functions of matrices, Proc. Amer. Math. Soc, 11 (1960), 97–101.Google Scholar
4. Rinehart, R. F., The equivalence of definitions of a matric function, Amer. Math. Monthly, 62 (1955), 395–414.Google Scholar
5. Rinehart, R. F., Intrinsic functions on matrices, Duke Math. J., 28 (1961), 291–300.Google Scholar
6. Rinehart, R. F., Differentiate intrinsic functions of complex matrices, Proc. Amer. Math. Soc., 12 (1961), 565–573.Google Scholar
7. Ringleb, F., Beiträge zur Funktionentheorie in hyperkomplexen Systemen, Rend. Circ. Mat. Palermo, 57 (1933), 311–340.Google Scholar
8. Townsend, E. J., Functions of a complex variable (New York, 1915).Google Scholar
9. Wilson, J. C. and Rinehart, R. F., Two types of differentiability of functions on algebras, Rend. Circ. mat. Palermo, 11 (1962), 204–216.Google Scholar