Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-13T06:33:59.082Z Has data issue: false hasContentIssue false
  • English
  • Français

Parametric Representation of Univalent Mappings in Several Complex Variables

Published online by Cambridge University Press:  20 November 2018

Ian Graham ,
Hidetaka Hamada  and
Gabriela Kohr
Ian Graham
Affiliation:
Department of Mathematics University of Toronto Toronto, Ontario M5S 3G3, e-mail: graham@math.toronto.edu
Hidetaka Hamada
Affiliation:
Faculty of Engineering Kyushu Kyoritsu University 1-8 Jiyugaoka, Yahatanishi-ku Kitakyushu 807-8585 Japan, email: hamada@kyukyo-u.ac.jp
Gabriela Kohr
Affiliation:
Faculty of Mathematics Babeş-Bolyai University 1 M. Kogălniceanu Str. 3400 Cluj-Napoca Romania, email: gkohr@math.ubbcluj.ro
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $B$ be the unit ball of 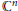${{\mathbb{C}}^{n}}$ with respect to an arbitrary norm. We prove that the analog of the Carathéodory set, i.e. the set of normalized holomorphic mappings from $B$ into 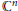${{\mathbb{C}}^{n}}$ of “positive real part”, is compact. This leads to improvements in the existence theorems for the Loewner differential equation in several complex variables. We investigate a subset of the normalized biholomorphic mappings of $B$ which arises in the study of the Loewner equation, namely the set 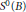${{S}^{0}}\left( B \right)$ of mappings which have parametric representation. For the case of the unit polydisc these mappings were studied by Poreda, and on the Euclidean unit ball they were studied by Kohr. As in Kohr’s work, we consider subsets of 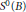${{S}^{0}}\left( B \right)$ obtained by placing restrictions on the mapping from the Carathéodory set which occurs in the Loewner equation. We obtain growth and covering theorems for these subsets of 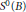${{S}^{0}}\left( B \right)$ as well as coefficient estimates, and consider various examples. Also we shall see that in higher dimensions there exist mappings in 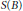$S(B)$ which can be imbedded in Loewner chains, but which do not have parametric representation.

Keywords

32H0230C45
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 54 , Issue 2 , 01 April 2002 , pp. 324 - 351
Copyright
Copyright © Canadian Mathematical Society 2002

References

[Ba-Fi-Go] Barnard, R. W., FitzGerald, C. H. and Gong, S., The growth and 1/4-theorems for starlike functions in Cn . Pacific J. Math. 150(1991), 13-22.Google Scholar
[Bec1] Becker, J., Löwnersche differentialgleichung und quasikonform fortsetzbare schlichte funktionen. J. Reine Angew. Math. 255 (1972), 23–43.Google Scholar
[Bec2] Becker, J., Über die Lösungsstruktur einer differentialgleichung in der konformen Abbildung. J. Reine Angew. Math. 285 (1976), 66–74.Google Scholar
[Che-Re] Chen, H. B. and Ren, F., Univalence of holomorphic mappings and growth theorems for close-to starlike mappings in finitely dimensional Banach spaces. Acta Math. Sinica (N.S.) 10(1994), Special Issue, 207–214.Google Scholar
[Chu] Chuaqui, M., Applications of subordination chains to starlike mappings in Cn . Pacific J. Math. 168 (1995), 33–48.Google Scholar
[Fi-Th] FitzGerald, C. H. and Thomas, C., Some bounds on convex mappings in several complex variables. Pacific J. Math. 165 (1994), 295–320.Google Scholar
[Go1] Gong, S., Convex and Starlike Mappings in Several Complex Variables. Kluwer Acad. Publ., 1998.Google Scholar
[Go2] Gong, S., The Bieberbach Conjecture. Amer. Math. Soc. Intern. Press, 1999.Google Scholar
[Gr-Ha-Ko-Su] Graham, I., Hamada, H., Kohr, G. and Suffridge, T., Extension operators for locally univalent mappings. Michigan Math. J., to appear.Google Scholar
[Gr-Ko] Graham, I. and Kohr, G., Univalent mappings associated with the Roper-Suffridge extension operator. J. Analyse Math. 81 (2000), 331–342.Google Scholar
[Gr-Ko-Ko] Graham, I., Kohr, G. and Kohr, M., Loewner chains and the Roper-Suffridge extension operator. J. Math. Anal. Appl. 247 (2000), 448–465.Google Scholar
[Gu] Gurganus, K., Φ-like holomorphic functions in Cn . Trans. Amer.Math. Soc. 205 (1975), 389–406.Google Scholar
[Ha1] Hamada, H., The growth theorem of convex mappings on the unit ball of Cn . Proc. Amer. Math. Soc. 127 (1999), 1075–1077.Google Scholar
[Ha2] Hamada, H., Starlike mappings on bounded balanced domains with C∞-plurisubharmonic defining functions. Pacific J. Math. 194 (2000), 359–371.Google Scholar
[Ha-Ko1] Hamada, H. and Kohr, G., Subordination chains and the growth theorem of spirallike mappings. Mathematica (Cluj) 42(65)(2000), 155–163.Google Scholar
[Ha-Ko2] Hamada, H. and Kohr, G., Subordination chains and univalence of holomorphic mappings on bounded balanced pseudoconvex domains. Ann. Univ. Mariae Curie-Skłodowski Sect. A 55 (2001), 61–80.Google Scholar
[Ha-Ko3] Hamada, H. and Kohr, G., Growth and distortion results for convex mappings in infinite dimensional spaces. Complex Variables Theory Appl., to appear.Google Scholar
[Ha-Ko4] Hamada, H. and Kohr, G., Quasiconformal extension of strongly starlike mappings on the unit ball of Cn . submitted.Google Scholar
[Ha-Ko-Li] Hamada, H., Kohr, G. and Liczberski, P., Starlike mappings of order α on the unit ball in complex Banach spaces. Glas. Mat. 36(56)(2001), 39–48.Google Scholar
[Har] Harris, L., The numerical range of holomorphic functions in Banach spaces. Amer. J. Math. 93 (1971), 1005–1019.Google Scholar
[Har-Re-Sh] Harris, L., Reich, S. and Shoikhet, D., Dissipative holomorphic functions, Bloch radii, and the Schwarz lemma. J. Anal.Math. 82 (2000), 221–232.Google Scholar
[He-Sh] Hengartner, W. and Schober, G., On schlicht mappings to domains convex in one direction. Comment. Math. Helv. 45 (1970), 303–314.Google Scholar
[Ka] Kato, T., Nonlinear semigroups and evolution equations. J. Math. Soc. Japan 19 (1967), 508–520.Google Scholar
[Ko1] Kohr, G., On some best bounds for coefficients of subclasses of biholomorphic mappings in Cn . Complex Variables Theory Appl. 36 (1998), 261–284.Google Scholar
[Ko2] Kohr, G., On starlikeness and strongly-starlikeness of order alpha in Cn . Mathematica (Cluj) 40(63)(1998), 95–109.Google Scholar
[Ko3] Kohr, G., The method of Löwner chains used to introduce some subclasses of biholomorphic mappings in Cn . Rev. Roumaine Math. Pures Appl., to appear.Google Scholar
[Ko-Li] Kohr, G. and Liczberski, P., Univalent Mappings of Several Complex Variables. Cluj University Press, 1998.Google Scholar
[Ku-Po] Kubicka, E. and Poreda, T., On the parametric representation of starlike maps of the unit ball in Cn into Cn . Demonstratio Math. 21 (1988), 345–355.Google Scholar
[Na] Narasimhan, R., Several Complex Variables. Chigago Lectures in Mathematics, 1971.Google Scholar
[Pf] Pfaltzgraff, J. A., Subordination chains and univalence of holomorphic mappings in Cn . Math. Ann. 210 (1974), 55–68.Google Scholar
[Pf-Su1] Pfaltzgraff, J. A. and Suffridge, T. J., Close-to-starlike holomorphic functions of several variables. Pacific J. Math. 57 (1975), 271–279.Google Scholar
[Pf-Su2] Pfaltzgraff, J. A. and Suffridge, T. J., An extension theorem and linear invariant families generated by starlike maps. Ann.Mariae Curie-Skłodowska Sect. A 53 (1999), 193–207.Google Scholar
[Pf-Su3] Pfaltzgraff, J. A. and Suffridge, T. J., Norm order and geometric properties of holomorphic mappings in Cn . J. Analyse Math. 82 (2000), 285–313.Google Scholar
[Po] Pommerenke, C., Univalent Functions. Vandenhoeck & Ruprecht, Göttingen, 1975.Google Scholar
[Por1] Poreda, T., On the univalent holomorphic maps of the unit polydisc of Cn which have the parametric representation, I—the geometrical properties. Ann. Univ. Mariae Curie-Skłodowska Sect. A 41 (1987), 105–113.Google Scholar
[Por2] Poreda, T., On the univalent holomorphic maps of the unit polydisc of Cn which have the parametric representation, II—necessary and sufficient conditions. Ann. Univ. Mariae Curie-Skłodowska Sect. A 41 (1987), 114–121.Google Scholar
[Por3] Poreda, T., On the univalent subordination chains of holomorphic mappings in Banach spaces. Comment. Math. 128 (1989), 295–304.Google Scholar
[Ro-Su1] Roper, K. and Suffridge, T., Convex mappings on the unit ball of Cn . J. Analyse Math. 65 (1995), 333–347.Google Scholar
[Ro-Su2] Roper, K. and Suffridge, T., Convexity properties of holomorphic mappings in Cn . Trans. Amer.Math. Soc. 351 (1999), 1803–1833.Google Scholar
[Ru] Rudin, W., Function Theory on the Unit Ball of Cn . Springer Verlag, New York, 1980.Google Scholar
[Su1] Suffridge, T. J., The principle of subordination applied to functions of several variables. Pacific J. Math. 33 (1970), 241–248.Google Scholar
[Su2] Suffridge, T. J., Starlike and convex maps in Banach spaces. Pacific J. Math. 46 (1973), 474–489.Google Scholar
[Su3] Suffridge, T. J., Starlikeness, convexity and other geometric properties of holomorphic maps in higher dimensions. Lecture Notes in Math. 599 (1976), 146–159.Google Scholar
[Su4] Suffridge, T. J., Biholomorphic mappings of the ball onto convex domains. Abstract of papers presented to Amer. Math. Soc. 11(66)(1990), p. 46.Google Scholar