Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T09:53:13.344Z Has data issue: false hasContentIssue false
  • English
  • Français

Perforated Ordered K0-Groups

Published online by Cambridge University Press:  20 November 2018

George A. Elliott  and
Jesper Villadsen
George A. Elliott
Affiliation:
Department of Mathematics, Universitetsparken 5, 2100 Copenhagen Ø, Denmark Department of Mathematics, University of Toronto Toronto, Ontario M5S 3G3 and The Fields Institute for Research in Mathematical Sciences, 222 College Street, Toronto, Ontario M5T 3J1
Jesper Villadsen
Affiliation:
Department of Mathematics, Odense University, 5230 Odense M, Denmark Department of Mathematics, University of Toronto Toronto, Ontario M5S 3G3 and The Fields Institute for Research in Mathematical Sciences, 222 College Street, Toronto, Ontario M5T 3J1
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

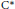A simple ${{C}^{*}}$-algebra is constructed for which the Murray-von Neumann equivalence classes of projections, with the usual addition—induced by addition of orthogonal projections—form the additive semigroup

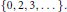$$\left\{ 0,\,2,\,3,\ldots \right\}.$$

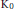(This is a particularly simple instance of the phenomenon of perforation of the ordered ${{K}_{0}}$-group, which has long been known in the commutative case—for instance, in the case of the four-sphere—and was recently observed by the second author in the case of a simple 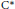${{C}^{*}}$-algebra.)

Keywords

46L3546L80
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 52 , Issue 6 , 01 December 2000 , pp. 1164 - 1191
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Blackadar, B., K-theory for Operator Algebras. Mathematical Sciences Research Institute Monographs 5, Springer-Verlag, New York, 1986.Google Scholar
[2] Bratteli, O., Inductive limits of finite dimensional C*-algebras. Trans. Amer. Math. Soc. 171(1972), 195–234.Google Scholar
[3] Dixmier, J., On some C*-algebras considered by Glimm. J. Funct. Anal. 1(1967), 182–203.Google Scholar
[4] Effros, E. G., Handelman, D. E. and Shen, C.-L., Dimension groups and their affine representations. Amer. J. Math. 102(1980), 385–407.Google Scholar
[5] Elliott, G. A., An invariant for simple C*-algebras. In: Invited Papers/Articles sollicités, CanadianMathematical Society 1945–1995, Vol. 3 (eds. Carrell, J. B. and Murty, R.), Canadian Mathematical Society, Ottawa, 1996, 61–90.Google Scholar
[6] Elliott, G. A. and Rørdam, M., Classification of certain infinite simple C*-algebras, II. Comment. Math. Helv. 70(1995), 615–638.Google Scholar
[7] Elliott, G. A. and Thomsen, K., The state space of the K0-group of a simple separable C*-algebra. Geom. Funct. Anal. 4(1994), 522–538.Google Scholar
[8] Husemoller, D., Fibre Bundles. McGraw–Hill, New York, 1966.Google Scholar
[9] Phillips, N. C., Approximation by unitaries with finite spectrum in purely infinite simple C*-algebras. J. Funct. Anal. 120(1994), 98–106.Google Scholar
[10] Rosenberg, J. and Schochet, C., The Künneth theorem and the universal coefficient theorem for Kasparov’s generalized K-functor. Duke Math. J. 55(1987), 431–474.Google Scholar
[11] Rørdam, M., Classification of certain infinite simple C*-algebras. J. Funct. Anal. 131(1995), 415–458.Google Scholar
[12] Villadsen, J., Simple C*-algebras with perforation. J. Funct. Anal. 154(1998), 110–116.Google Scholar