Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T09:05:59.615Z Has data issue: false hasContentIssue false
  • English
  • Français

Peter–Weyl Iwahori Algebras

Part of: Lie groups

Published online by Cambridge University Press:  21 June 2019

Dan Barbasch  and
Allen Moy
Dan Barbasch
Affiliation:
Department of Mathematics, Malott Hall, Cornell University, Ithaca, NY 14853–0099, USA Email: barbasch@math.cornell.edu
Allen Moy
Affiliation:
Department of Mathematics, The Hong Kong University of Science and Technology, Clear Water Bay Road, Hong Kong Email: amoy@ust.hk
Get access Rights & Permissions [Opens in a new window]

Abstract

The Peter–Weyl idempotent 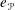$e_{\mathscr{P}}$ of a parahoric subgroup 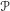$\mathscr{P}$ is the sum of the idempotents of irreducible representations of 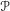$\mathscr{P}$ that have a nonzero Iwahori fixed vector. The convolution algebra associated with 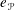$e_{\mathscr{P}}$ is called a Peter–Weyl Iwahori algebra. We show that any Peter–Weyl Iwahori algebra is Morita equivalent to the Iwahori–Hecke algebra. Both the Iwahori–Hecke algebra and a Peter–Weyl Iwahori algebra have a natural conjugate linear anti-involution $\star$, and the Morita equivalence preserves irreducible hermitian and unitary modules. Both algebras have another anti-involution, denoted by $\bullet$, and the Morita equivalence preserves irreducible and unitary modules for $\bullet$.

Keywords

convolution algebraIwahori–Hecke algebraidempotentMorita equivalenceparahoric subgroupPeter–Weyl idempotent⋆-algebra

MSC classification

Primary: 22E50: Representations of Lie and linear algebraic groups over local fields
Secondary: 22E35: Analysis on $p$-adic Lie groups
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 5 , October 2020 , pp. 1304 - 1323
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Author D.B. is partly supported by NSA grant H98230-16-1-0006. Author A.M. is partly supported by Hong Kong Research Grants Council grant CERG #16301915.

References

Adams, J., van Leuween, M., Trapa, P., and Vogan, D., Unitary representations of real reductive groups. 2012. arxiv:1212.2192v2Google Scholar
Barbasch, D. and Ciubotaru, D., Star operations for affine Hecke algebras. 2015. arxiv:1504.04361Google Scholar
Barbasch, D. and Ciubotaru, D., Unitary Equivalences for reductive p-adic groups. Amer. J. Math. 135(2013), 1633–1674. https://doi.org/10.1353/ajm.2013.0048CrossRefGoogle Scholar
Barbasch, D., Ciubotaru, D., and Moy, A., An Euler–Poincaré formula for a depth zero Bernstein projector. Represent. Theory 23(2019), 154–187. https://doi.org/10.1090/ert/525CrossRefGoogle Scholar
Barbasch, D. and Moy, A., A unitarity criterion for p-adic groups. Invent. Math. 98(1989), no. 1, 19–38. https://doi.org/10.1007/BF01388842CrossRefGoogle Scholar
Barbasch, D. and Moy, A., Reduction to real infinitesimal character in Hecke algebras. J. Amer. Math. Soc. 6(1993), no. 3, 611–635. https://doi.org/10.2307/2152779CrossRefGoogle Scholar
Bushnell, C. J. and Kutzko, P. C., Smooth representations of reductive p-adic groups: structure theory via types. Proc. London Math. Soc. 77(1998), 582–634. https://doi.org/10.1112/S0024611598000574CrossRefGoogle Scholar
Ciubotaru, D., Types and unitary representations of reductive p-adic groups. Invent. Math. 213(2018), 237–269. https://doi.org/10.1007/s00222-018-0790-4CrossRefGoogle ScholarPubMed
Harish-Chandra, Eisenstein series over finite fields. In: Functional analysis and related fields (Proc. Conf. M. Stone, Univ. Chicago, Chicago, Ill., 1968). Springer, 1970, pp. 76–88.Google Scholar
Lam, T. Y., Lectures on modules and rings. Graduate Texts in Mathematics, 189, Springer-Verlag, New York, 1999. https://doi.org/10.1007/978-1-4612-0525-8CrossRefGoogle Scholar
Lusztig, G., Some examples of square integrable representations of semisimple p-adic groups. Trans. Amer. Math. Soc. 277(1983), no. 2, 623–653. https://doi.org/10.2307/1999228Google Scholar
Lusztig, G., Affine Hecke algebras and their graded version. J. Amer. Math. Soc. 2(1989), 599–635. https://doi.org/10.2307/1990945CrossRefGoogle Scholar
Moy, A. and Prasad, G., Unrefined minimal K-types for p-adic groups. Invent. Math. 116(1994), no. 1–3, 393–408. https://doi.org/10.1007/BF01231566CrossRefGoogle Scholar
Moy, A. and Prasad, G., Jacquet functors and unrefined minimal K-types. Comment. Math. Helv. 71(1996), no. 1, 98–121. https://doi.org/10.1007/BF02566411CrossRefGoogle Scholar
Opdam, E., Harmonic analysis for certain representations of graded Hecke algebras. Acta. Math. 175(1995), 75–121. https://doi.org/10.1007/BF02392487CrossRefGoogle Scholar
Rieffel, M., Morita Equivalence for [[()[]mml:mi[]()]]𝘊[[()[]/mml:mi[]()]]⋆-algebras and W ⋆-algebras. J. Pure Appl. Algebra 5(1974), 51–96. https://doi.org/10.1016/0022-4049(74)90003-6CrossRefGoogle Scholar