Published online by Cambridge University Press: 20 November 2018
If K is a compact subset of Cn,  will denote the polynomial hull of K:
will denote the polynomial hull of K:
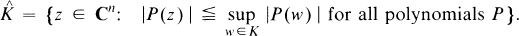
 arises in the study of uniform algebras as the maximal ideal space of the algebra P(K) of uniform limits on K of polynomials (see [3]). The condition
arises in the study of uniform algebras as the maximal ideal space of the algebra P(K) of uniform limits on K of polynomials (see [3]). The condition  (K is polynomially convex) is a necessary one for uniform approximation on K of continuous functions by polynomials (P(K) = C(K)). If K is not polynomially convex, the question of existence of analytic structure in
(K is polynomially convex) is a necessary one for uniform approximation on K of continuous functions by polynomials (P(K) = C(K)). If K is not polynomially convex, the question of existence of analytic structure in 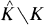 is of particular interest. For n = 1,
is of particular interest. For n = 1,  is the union of K and the bounded components of C\K. The determination of
is the union of K and the bounded components of C\K. The determination of  in dimensions greater than one is a more difficult problem. Among the special classes of compact sets K whose polynomial hulls have been determined are those invariant under certain group actions on Cn.
in dimensions greater than one is a more difficult problem. Among the special classes of compact sets K whose polynomial hulls have been determined are those invariant under certain group actions on Cn.