Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ignatenko, V. F.
1996.
Invariants of finite and infinite groups generated by reflections.
Journal of Mathematical Sciences,
Vol. 78,
Issue. 3,
p.
334.


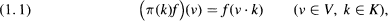
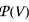 of polynomial functions on
of polynomial functions on 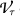 of
of 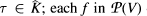 can then be written as
can then be written as 