Article contents
Power-Rich and Power-Deficient LCA Groups
Published online by Cambridge University Press: 20 November 2018
Extract
In [4], Edwin Hewitt denned a-rich LCA (i.e., locally compact abelian) groups and classified them by their algebraic structure. In this paper, we study LCA groups with some properties related to a-richness. We define an LCA group G to be power-rich if for every open neighbourhood V of the identity in G and for every integer n > 1, λ(nV) > 0, where nV = {nx ∈ G : x ∈ V} and λ is a Haar measure on G. G is power-meagre if for every integer n > 1, there is an open neighbourhood V of the identity, possibly depending on n, such that λ(nV) = 0. G is power-deficient if for every integer n > 1 and for every open neighbourhood V of the identity such that 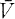 is compact,
is compact, 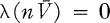 . G is dual power-rich if both G and Ĝ are power-rich. We define dual power-meagre and dual power-deficient groups similarly.
. G is dual power-rich if both G and Ĝ are power-rich. We define dual power-meagre and dual power-deficient groups similarly.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1981
References
- 4
- Cited by


